Stufenmodelle für den inklusiven Mathematikunterricht

Andrea Bethge, Marion Donath-Frense, Ute Geiling,
Martina Hehn-Oldiges, Susanne Schnepel, Christin Tellisch

Inhaltsverzeichnis

Abkürzungsverzeichnis
Einleitung
Tabellarische Stufenmodelle
3.1: Stufenmodell zum Teilbereich: Zahl und Operation
3.2: Größen und Messen
3.3: Raum und Form
3.4: Daten und Zufall
3.5: Strukturen und funktionaler Zusammenhang
Führerscheine für die Hand der Kinder
Exemplarische Entwürfe für das Lernen am gemeinsamen Gegenstand
Entwürfe für die Arbeit an Themen und Interessen der Kinder
Kommentierter Überblick über Stufenmodelle
7.1: Basaler Zugang zum mathematischen Kompetenzerwerb
7.2: Elementarer Zugang zum mathematischen Kompetenzerwerb
7.3: Primarer Zugang zum mathematischen Kompetenzerwerb
7.4: Sekundarer Zugang zum mathematischen Kompetenzerwerb
7.5: Weitere Stufenmodelle
Literaturverzeichnis

1. Abkürzungsverzeichnis

ebd. = ebenda
KMK = Kultusministerkonferenz
ReMi = Reckahner Modelle zur inklusiven Unterrichtsplanung
vgl. = vergleiche

2. Einleitung

Der Lernbereich Mathematik umfasst Schwerpunkte grundlegender Bildung, die für alle Lernenden von zentraler Bedeutung sind. Laut KMK (2022) wird mathematische Bildung eingeteilt in fünf Teilbereiche:

Zahl und Operation
Größen und Messen
Daten und Zufall
Raum und Form
Muster, Strukturen und funktionale Zusammenhänge

In inklusiven Schulen findet Lernen in heterogenen Lerngruppen statt. Daraus folgt, dass Lehrkräfte die Lernausgangslagen der einzelnen Schülerinnen und Schüler erkunden und dazu passende individuelle Lernanbausteine anbieten. So soll ermöglicht werden, dass jedes Kind und jeder Jugendliche in eigener Geschwindigkeit lernen kann. Erprobte didaktische Arbeitsweisen dazu sind unter anderem Freiarbeit, Lernbüroarbeit, Projektarbeit und das Differenzierte Lernen am gemeinsamen Gegenstand. Zugleich wird die Klassengemeinschaft gepflegt.

Im Rahmen der Projekts REMI (Reckahner Modelle zur inklusiven Unterrichtsplanung) werden Hilfsmittel für inklusiven Unterricht bereitgestellt. Sie umfassen folgende Dokumente: Die Beschreibung des REMI-Mathematik-Modells in dieser Einleitung, die Mathematik Stufenmodelle in Tabellenform, Führerscheine für die Hand der Kinder, exemplarische Entwürfe für das Lernen am gemeinsamen Gegenstand, Entwürfe für die Arbeit an Themen und Interessen der Kinder und Jugendlichen, einen kommentierten Überblick über die REMI-Zugänge zum basalen, elementaren, primaren und sekundaren mathematischen Lernen sowie über weitere Stufenmodelle. Abschließend folgt ein Literaturverzeichnis.

Stufenmodelle

Als für inklusiven Unterricht zentrales Hilfsmittel werden im REMI-Projekt fachdidaktische Stufenmodelle zur Verfügung gestellt, die alle Lernausgangslagen bis hin zum Mittleren Bildungsabschluss umfassen. Die tabellarischen Stufenmodelle beziehen sich darum auf basale, elementare, primare und sekundare Zugänge (siehe die ausführlichen Ausführungen dazu in Kapitel 7. dieses Textes zu REMI-Mathematik). Sie dienen dazu, in inklusiven Klassen die individuell äußerst heterogenen Lernausgangslagen zu erkennen, zu benennen und jeweils dazu passende individuelle mathematische Lernmaterialien anzubieten.

In Einklang mit diesem Ziel ist das vorliegende Kompetenzstufenmodell (siehe Kapitel 3) in drei Spalten untergliedert. Diese enthalten die Beschreibung der Kompetenzstufe in Erwachsenensprache, in Kindersprache und in der dritten Spalte die zu jeder Stufe passenden pädagogischen Angebote. Diese Lernbausteine dienen dazu, das Erreichte zu stabilisieren und die nächste Stufe zu erreichen.

Am linken Rand der Tabelle wird jeweils farbig angezeigt, welchem der vier Zugänge (elementar, basal, primar oder sekundar) die Kompetenzen grundsätzlich zuzuordnen sind. Damit soll erreicht werden, dass die individuellen Potenziale jedes einzelnen Kindes im differenzierenden Mathematikunterricht entdeckt und gefördert werden. Dabei gibt es auch Kompetenzen, die mehreren Zugängen zugeordnet werden z.B. elementar und primar.
Die stufenförmige Anordnung soll nicht den Anschein erwecken, dass Kompetenzen der Lernenden nacheinander strikt linear aufgebaut werden oder dass jede Stufe gleich viel Zeit und Aufwand brauchen würde. Dies würde nicht den realen Lernprozessen und der Heterogenität der Kinder entsprechen, sondern ist lediglich der übersichtlichen Abbildbarkeit geschuldet.

Das Stufenmodell kann zur Einschätzung des Kompetenzstandes von Lernenden im Fachbereich der Mathematik ausgehend von basalen Vorerfahrungen und Fähigkeiten von der basalen Entwicklung bis zu Kompetenzen für den Mittleren Abschluss genutzt werden. Diese Diagnostik kann seitens der Pädagog_innen vor allem durch alltägliche Beobachtungen und Gespräche realisiert werden. Die Ergebnisse können mithilfe der in den Spalten 1 und 2 dargelegten Formulierungen transparent gemacht werden.

Die Lernenden können sich dabei zudem durch Selbsteinschätzungen und mithilfe der aus Lernendenperspektive formulierten Aussagen im Stufenmodell (Spalte 2) einordnen, wenn ihnen diese in geeigneten Formen zur Verfügung gestellt werden. Dabei ist es immer wieder wichtig, dass die Pädagog_innen frühzeitig die in einer inklusiven Klasse vorfindlichen Lernausgangslagen sondieren, dazu passende Lernangebote vorbereiten und bereitstellen.

Teilbereiche

Im Folgenden werden Stufenmodelle zu den vier Teilbereichen Zahl und Operationen, Größen und Messen, Raum und Form sowie Daten und Zufall für basale, elementare, primare und sekundare Bildungszugänge ausgeführt. Der fünfte Teilbereich, der in der Primarstufe in einigen Lehrplänen der Primarstufe Muster und Strukturen heißt, wird vom basalen bis zum primaren Lernzugang als inhaltsübergreifender Kompetenzbereich in die vier genannten Teilbereiche eingebunden. In der Auseinandersetzung mit mathematischen Mustern und Darstellungen werden mathematisch relevanten Strukturen in allen inhaltsbezogenen Teilbereichen erkundet. Lernende entdecken funktionale Beziehungen und Gesetzmäßigkeiten zwischen Zahlen, Formen, Größen, die sie erkennen, beschreiben und darstellen: im Bereich Zahlen und Operationen (ZuO): Strukturen in arithmetischen Mustern (Zahldarstellungen, Zahldarstellungen, Aufgabenfolgen, Darstellungsmitteln), im Bereich Größen und Messen (GuM): Strukturen beim Lösen von Sachaufgaben usw., beim Erwerb geometrischen Grundwissens im Bereich Raum und Form (RuF), Strukturen in geometrischen Abbildungen in der Umwelt und Mustern, beim Erstellen von Übersichten im Bereich Daten und Zufall (DuZ): Lösen von einfachen kombinatorischen Fragestellungen durch systematisches Probieren und Vorgehen mit Hilfe von Abbildungen (Skizzen, Tabellen usw.) (vgl. KMK 2022, S. 13 – 18). In den Stufenmodellen wird zu Beginn des jeweiligen inhaltsbezogenen Teilbereichs auf die Bezüge zum Teilbereich Muster, Strukturen und funktionale Zusammenhänge (MSufZ) verwiesen.

Für die Sekundarstufe ist der Teilbereich Strukturen und funktionaler Zusammenhang in den Bildungsstandards als eigene Leitidee aufgeführt und funktionale Zusammenhänge sind ein wesentliches Thema in Klasse 5-10. Deshalb wurde ein Stufenmodell zum Teilbereich Strukturen und funktionaler Zusammenhang, das sich nur auf den sekundaren Zugang bezieht, entwickelt.

Basale Anfänge der mathematischen Kompetenzentwicklung

Die basalen Anfänge der Kompetenzentwicklung (basal und Übergang basal-elementar) sind in der Tabelle in Bezug auf alle Teilbereiche der Bildungsstandards identisch. Es für die Anfänge der mathematischen Bildung sinnvoll, die prozessbezogenen wie auch die inhaltsbezogenen Vorläuferfähigkeiten für den Erwerb mathematischer Kompetenzen in ihrem ganzheitlichen Zusammenwirken zu beschreiben, denn lebensproblemorientierte Alltags- und Spielhandlungen führen zu Fragestellungen und grundlegenden Erfahrungen für mathematisches Handeln mit Zahlen, Operationen, Raum, Form, Größen, Messen, Strukturen usw., die sich nur künstlich teilbereichsbezogen aufsplitten lassen. Die elementaren Zugänge werden dann bereits teilbereichsspezifisch ausdifferenziert.
Mit dem Konzept eines „anschlussfähigen Mathematikbegriffs“, das Schäfer (2020) für Lernende mit dem Förderschwerpunkt geistige Entwicklung (oder mit zugeschriebener geistiger Behinderung) zur Verfügung stellt, können vorzahlige und zahlige Kompetenzen ab der basalen Stufe den Teilbereichen der Bildungsstandards zugeordnet werden. Dieses Vorgehen löst das bisherige Konzept der Notwendigkeit der Festigung pränumerischer Fähigkeiten vor dem zahligen Handeln ab und verweist auf die Notwendigkeit der Parallelität von vorzahligen und zahligen Lernprozessen für die Mathematisierung konkreter Lebensweltbezüge (Schäfer 2020, S. 14 – 31). Beispiele für relevante Vorerfahrungen für die einzelnen Kompetenzbereiche des Unterrichtsfachs Mathematik sind:

Teilbereich: Zahl und Operation (ZuO): Hier ist die grundsätzliche Fähigkeit zur Unterscheidung von Merkmalen (wie z.B. Beschaffenheit, Form, Farbe usw.) zu benennen. Sie ermöglicht es später, Mengen zu bilden (Sortieren, Klassifizieren), zu vergleichen, zu zerlegen und in Beziehung zu setzen (viel – wenig, mehr – weniger, dazu tun – wegnehmen).

Teilbereich: Größen und Messen (GuM): Als Voraussetzungen für diesen Teilbereich der Mathematik kann die Fähigkeit zur Unterscheidung von Merkmalen wie z.B. von Größe und Gewicht (leicht – schwer, voll – leer) angesehen werden sowie die Fähigkeit unterschiedliche Behältnisse zu unterscheiden.

Teilbereich: Raum und Form: (RuF) Raumerfahrungen im Nahfeld sind z.B.: sich selbst im Raum erfahren und orientieren, die Anordnung von Dingen im Raum erfahren (sie befinden sich oben – unten, vorne – hinten, innen – außen, nah – weit usw.) sowie die Unterscheidung von Merkmalen und der Gestalt der Dinge (Kugeln sind rund, rollen weg, es gibt eckige Schachteln usw.). Sie stellen vorzahlige Voraussetzungen für diesen Teilbereich dar.

Teilbereich: Muster, Strukturen und funktionaler Zusammenhang (MSufZ): Erfahrungen mit Strukturen und funktionalen Zusammenhängen werden durch das Erkennen von Gesetzmäßigkeiten in räumlichen Anordnungen gemacht (z.B. Stellen des Stuhlkreises in derselben Weise, dieselben Muster beim Tisch-Decken: Teller und Besteck anordnen).

Teilbereich: Daten und Zufall (DuZ): Regelmäßige oder ritualisierte Abläufe führen zu Erfahrungen mit Zeit und Wiederholungen (z.B. nach der Ankunft folgt eine Begrüßung, es gibt Pausen, Versorgungen wie Essen und Körperpflege finden zu bestimmten Zeiten statt), die durch Pläne, Kalender usw. abgebildet werden.

Die Ausführungen zu den Teilbereichen ab der primaren Stufe beziehen sich auf die Bildungsstandards der KMK (2022).

3. Tabellarische Stufenmodelle

Für die Darstellung im Stufenmodell der inklusiven Unterrichtsplanung ist die Einteilung der Themen in Teilbereiche sinnvoll, um die Handhabbarkeit bei der Planung und Durchführung zu gewährleisten. Zusätzlich zur Übersicht von Kriesel wurden bezogen auf die Lehrpläne ausgehend von einer Lehrplanstufe (5. Jahrgangsstufe) die Lehrpläne für Ethik aller Bundesländer genau miteinander verglichen und die vorkommenden Kompetenzen/Themen in ein Raster eingeordnet und Themenblöcke identifiziert, die bei vielen Lehrplänen vorkommen. Daraufhin wurde einerseits abgeglichen, welcher Lehrplan die meisten dieser Themen identifiziert und andererseits überprüft, welche Lehrpläne mit einem Kompetenzmodell arbeiten, das klar offengelegt und nachvollziehbar dargestellt und dem wissenschaftlichen Diskurs angemessen ist. Der Lehrplan von Thüringen erwies sich in der Verwendung des Kompetenzmodells als für die weiterführende Arbeit am besten geeignet, da dieser einigermaßen in sich konsistent aufgebaut war und gleichzeitig den wissenschaftlichen Diskurs berücksichtigt. Das Kompetenzmodell von Thüringen wurde dementsprechend zu Grunde gelegt und Ergänzungen durch die weiteren Lehrpläne und wissenschaftliche Literatur vorgenommen. So ergab sich ein Überblick über wesentliche Kompetenzen und damit verwobene Inhalte.

Die Benennung der vier Teilbereiche, nach denen die Stufenmodelle gegliedert sind, wird im Folgenden leicht adaptiert vom Thüringer Lehrplan Grundschule entnommen (so wurde im dritten Themenbereich Religion integriert und im vierten Themenbereich der Faktor Zeit), was sich inhaltlich auch mit der Übersicht der Lehrpläne für Grundschule von Kriesel deckt. Die ersten drei Teilbereiche im Bereich der Grundschule entsprechen auch der Gliederung der ersten drei Bereiche für Sek I. Auffallend ist, dass der Bereich der Grundschule „Unsere Zeit, Umwelt und Natur“ in den Themenbereichen des Sekundarbereichs 1 nicht mehr aufscheint, sondern hier als vierter Bereich „Philosophische Ethik und Angewandte Ethik“ gesetzt ist. Im Sinne der aufbauenden Kompetenzen wird im Folgenden der vierte Themenbereich „Unsere Zeit, Umwelt und Natur“ auch für den Sekundarstufenbereich 1 fortgeführt und die „Philosophische Ethik und Angewandte Ethik“ in die vier Teilbereiche integriert.
Folgende Teilbereiche liegen dem folgenden Stufenmodell zugrunde:

Lernende in Individualität und Persönlichkeitsentwicklung (Ich – Was ist der Mensch?)
Lernende in sozialen Beziehungen (Ich und Wir – Was soll ich tun?)
Lernende im Verhältnis zu Kulturen, Religionen und Weltanschauungen (Wir und die Anderen – Was darf ich hoffen?)
Lernende im Verhältnis zur Umwelt und Zeit (Die Welt und ich – Was kann ich wissen?)

Wesentliche Kompetenzen und damit verschränkte Inhalte werden (großteils adaptiert) vom Thüringer Bildungsplan für Grund-, Haupt- und Realschule übernommen und den vier Themenbereichen zugeordnet. Darüber hinaus wurden innerhalb der jeweiligen Themenbereiche die Kompetenzen und Inhalte gebündelt und diesen den dazu passenden thematischen Überschriften zugeordnet.

Auch wenn sich die Grundstruktur des Thüringer Bildungsplans für Ethik als hilfreich erwies, sind viele Kompetenzen nicht in sich konsistent aufgebaut, die Themen wirken teilweise zufällig gesetzt. So wurden, nachdem der gesamte Thüringer Bildungsplan geclustert, Themenbereiche gebildet, um so eine erste Übersicht und Grundlage geschaffen wurde, im Abgleich mit weiteren Lehrplänen und theoretischen Ausarbeitungen (vgl. Roew/Kriesel 2017), entwicklungspsychologischen Erkenntnissen (u.a. Kohlberg 1995, Oser & Gmünder 1996, Erikson 1973, Fowler 2000, Heckhausen/Heckhausen 2010, Roth 2011) die Stufen weiter vertieft und adaptiert. Einzelne Themen wurden dadurch gestärkt, andere wurden entfernt, Kompetenzen näher ausdifferenziert und fehlende Schritte ergänzt. Die nun vorliegenden Teilbereiche wurden ausgehend von den Zielsetzungen und zu erwerbenden Kompetenzen im Ethikunterricht als geeignet erachtet, die Kompetenzen zu entwickeln, die für einen erfolgreichen Abschluss der Sek I notwendig sin.
Folgende Teilbereiche werden im Stufenmodell unter Berücksichtigung basaler, elementarer, primarer und sekundarer Zugänge beleuchtet:

Teilbereich A: Lernende in Individualität und Persönlichkeitsentwicklung

Übergeordnete Kompetenz: Lernende setzen sich mit eigenen Einstellungen und Handlungen auseinander und reflektieren, welche Handlungen sich moralisch rechtfertigen lassen.

Eigene Eigenschaften und Fähigkeiten einschätzen
Umgang mit Gefühlen
Umgang mit Wünschen
Wahrnehmung und Vorurteile
Auseinandersetzung mit Leben und Tod
Auseinandersetzung mit Freiheit und Abhängigkeit
Gewissensbildung
Gesundheit – Selbstsorge
Mediengebrauch
Informationsgewinn

Die zugehörigen Tabellen zu Teilbereich A finden Sie unter Punkt 3

Teilbereich B: Lernende in sozialen Beziehungen

Übergeordnete Kompetenz: Lernende reflektieren die Notwendigkeit des respektvollen Miteinanders und setzen sich mit den Menschenrechten als Grundlage des Werte- und Normensystems auseinander.

Menschenwürde – Menschenrechte – Kinderrechte
Freundschaften
Zusammenleben in Gemeinschaften
Regeln des Zusammenlebens
Respektvoller Umgang miteinander
Umgang mit Konflikten
Reflexion von Glück und Sinn
Reflexion über Liebe
Auseinandersetzung mit Gerechtigkeit
Entscheidungen bei ethisch schwierigen Fragen
Kommunikation

Die zugehörigen Tabellen zu Teilbereich B finden Sie unter Punkt 3

Teilbereich C: Lernende im Verhältnis zu Kulturen und Religionen

Übergeordnete Kompetenz: In der Auseinandersetzung mit unterschiedlichen Religionen und Kulturen respektieren die Lernenden religiöse, kulturelle und weltanschauliche Vielfalt und reflektieren ihre eigenen Werte.

Feste
Unterschiedliche Religionen – Christentum
Unterschiedliche Religionen – Judentum
Unterschiedliche Religionen – Islam
Weitere Religionen
Religiöse und kulturelle Vielfalt
Wertvorstellungen begründen

Die zugehörigen Tabellen zu Teilbereich C finden Sie unter Punkt 3

Teilbereich D: Lernende in ihrem Verhältnis zur Umwelt und Zeit

Übergeordnete Kompetenz: In der Auseinandersetzung und in der Reflexion eigener Erfahrungen erkennen Lernende die Verantwortung des Menschen für die Natur und die Mitwelt und leiten daraus eigene Verhaltensregeln ab.

Umgang mit Natur
Umwelt- und Klimaschutz
Umgang mit Technik
Umgang mit Zeit

Die zugehörigen Tabellen zu Teilbereich D finden Sie unter Punkt 3

Wenn die Stufenmodelle auch unterschiedliche Kompetenzstufen abbilden und als lineare Abfolge dargestellt sind, können die einzelnen Schritte parallel ablaufen bzw. sich je nach Kind in der Reihenfolge verschieben.

Einige der benannten Kompetenzen sind nicht ausschließlich im Ethikunterricht, sondern auch in anderen Fächern zu bearbeiten. – Häufig gibt es auch Überschneidungen zu anderen Themenbereichen (bspw. Biologie, politische Bildung, Religion etc.)

Insbesondere bei Themen, bei denen Kinder und Jugendliche aufgefordert werden, ethische Themen auf ihr eigenes Leben hin zu reflektieren, ist besondere pädagogische Sensibilität gefragt. Bei allen Themen, aber hier in Besonderem, gilt, dass es stets freiwillig bleiben muss, was davon im Unterrichtsgeschehen mitgeteilt wird.

Grundlage für das Unterrichtsfach sind die Menschenrechte. Wenn diese nun detailliert als ein Themenbereich näher entfaltet werden, sind diese zugleich die normative Grundlage für die Bearbeitung der unterschiedlichen Themenbereiche.

Download
Stufenmodelle
Mathematik

3. Tabellarische Stufenmodelle

Tabelle 3.1 Stufenmodell zum Teilbereich: Zahl und Operation

Abkürzungen Tabellen: b = basal | e = elementar | p = primär | s = sekundär


					Teilbereich: Zahlen und Operationen (ZuO) Muster, Strukturen und funktionale Zusammenhänge im Teilbereich Zahlen und Operationen Arithmetische strukturierte Zahldarstellungen finden sich in strukturierten Darstellungsmitteln (10er-, 20er-, Hunderterfeld, Zahlenhäuser, Stellenwerttafeln usw.) in der Zahlenfolge (Zahlwortreihe, Zahlenstrahl) und in Aufgabenfolgen (Zahlen schreiben, Anordnung der Zahlen, Operationszeichen, Links-, Rechtsorientierung usw.) Lernende können in den jeweiligen Zugängen in der handelnden Auseinandersetzung mit der Umwelt bestimmte Muster und strukturierte Abläufe erfahren. Ab dem primaren Zugang lernen sie diese zunehmend in Aufgabenfolgen und durch der Nutzung von Darstellungsmitteln erkennen. Dazu gehören Muster in der Addition, Subtraktion, Multiplikation, Division mit Kernaufgaben, die erkannt, beschrieben, weitergeführt oder verändert dargestellt werden können. Indem die Lernenden zunehmend die Beziehungen der Zahlen untereinander erkennen, können sie Gesetzmäßigkeiten und funktionale Zusammenhänge bei der Anwendung von Aufgabenformaten anwenden.		Pädagogische Angebote Lehrkräfte erläutern ab der primaren Stufe die Struktur der Darstellungsmittel, der Aufgabenfolge und bieten Lernanlässe (z.B. Zahlenhäuser, Zahlenstrahl, Zahlenfelder), die zum Austausch über die möglichen Muster und Gesetzmäßigkeiten anregen. Sie leiten Lernende dazu an, Rechengesetze zu erkennen, zu erklären und zu nutzen (KMK 2022, S. 14).
b	e	p	s	ILZ	Stufe in Erwachsenensprache	Stufe in Kindersprache	Lernbausteine
				1a	Sinnliche Welterkundung Allgemein-mathematische (prozessbezogene) Kompetenzen basieren auf einer aktiv-entdeckenden Auseinandersetzung durch Zufallshandlungen mit Dingen/Gegenständen Inhaltsbezogene mathematische Vorerfahrungen Die Lernenden handeln zufällig in ihrem Körper- und Nahfeld. Durch die Komplexität der Situation können sie basale Erfahrungen in den sich überschneidenden Kompetenzbereichen machen. Die Gestaltung des Nah- und Greiffelds ermöglicht ihnen das Lernen durch Berühren, Bewegen, Beobachten interessanter Eigenschaften und Merkmale: Raumerfahrungen durch Lagerungsorte (Rollstuhl, Little Room usw.), Raumbegrenzungen, räumliche Anordnung von Dingen (oben- unten, vorne – hinten, innen – außen) sind bedeutsam für den Kompetenzbereich Raum und Form (RuF), basale Vorerfahrungen durch regelmäßige und wiederholte zeitliche Abläufe und räumliche Angebote sind bedeutsam für die Kompetenzbereiche Muster, Strukturen und funktionale Zusammenhänge (MSufZ) sowie Daten und Zufall (DuZ), sinnliche Erfahrungen durch die Beschaffenheit von Dingen (einschließlich Geruch und Geschmack) mit weiteren unterschiedlichen Eigenschaften und Merkmalen (hart – weich, farbig, glatt, laut – leise, hell – dunkel usw.) Formen (rund – eckig) sind bedeutsam für den Kompetenzbereich Raum und Form (RuF), Erfahrungen bei den Zufallshandlungen mit Gewicht, Größe, Entfernung (groß – klein, leicht – schwer, nah – weit) sind bedeutsam für den Kompetenzbereich Größen und Messen (GuM) Die benannten Erfahrungen ermöglichen die Entwicklung der Fähigkeit, Dinge grundsätzlich zu unterscheiden. Das ist wiederum eine Voraussetzung für das Bilden von Mengen (Sortieren) im Kompetenzbereich Zahl und Operation (ZuO)	Die Ausdrucksformen der Lernenden in den basalen Stufen sind überwiegend nonverbal. Die Formulierungen dienen der Einnahme der Perspektive von Lernenden. Ich kann, was um mich geschieht hören, sehen, spüren, riechen, schmecken, fühlen. Ich kann die Dinge, die ich zufällig ergreife, berühren, belecken und in Bewegung bringen. Dabei erfahre ich, dass sich Gegenstände und Materialien unterschiedlich anfühlen. Ich beginne, ganz bestimmte Personen, Gegenstände und Materialien, Muster, Formen zu bevorzugen und kann dies durch Zuwendung, Wiederholung, durch Mimik, Gestik und durch Laute zum Ausdruck bringen.	Gestaltung des Nah- und Greiffelds: Materialien und Gegenstände sind im Nah- und Greiffeld angebracht, die leicht berührt und bewegt werden können die Geräusche oder Lichteffekte auslösen die kontrastreiche Muster und Farben haben die aus unterschiedlichen Formen und Materialen bestehen Handlungen werden von Bezugspersonen und anderen Lernenden beobachtet und im Dialog gespiegelt. Beispiele in Hehn-Oldiges/Simon 2023 (bitte Datei verlinken) Materialien, die zu aktiven Wiederholungen anregen, werden gezielt angeboten und durch weitere, mit ähnlichen Eigenschaften ergänzt. ...
				1b	Welterkundung durch unspezifisches Operieren Aktive Wiederholungen erweitern die allgemein-mathematische Kompetenzen durch die aktiv-entdeckenden Auseinandersetzung mit Dingen/Gegenständen Inhaltsbezogene mathematische Vorerfahrungen Interessante Effekte durch Dinge und Materialien im Körper-, Nah- und Greiffeld werden von den Lernenden aktiv wiederholt und die inhaltsbezogenen Vorerfahrungen zu den Kompetenzbereichen (MSufZ, RuF, GuM, ZuO, DuZ) können sich jeweils festigen und erweitern. Dinge/Gegenstände werden mit dem Mund, den Händen oder Füßen erkundet (Berühren, Klopfen, Werfen usw.). Erreichbare Materialien und Dinge ermöglichen so die aktive Wahrnehmung und zunehmende Unterscheidung von Gegenständen und deren Eigenschaften: Größe, Beschaffenheit, Form, Farbe, Klangeffekte, Geruch, Geschmack usw.	Ich kann Bewegungen, die es mir ermöglichen, für mich bedeutsame Dinge zu erreichen oder Effekte herbeizuführen, aktiv wiederholen. Ich kann diese Dinge mit dem Mund, den Händen und den Füßen durch Berühren, Klopfen, Werfen usw. immer genauer erkunden und so Größe, Beschaffenheit, Form, Farbe, Klangeffekte, Geruch, Geschmack usw. wahrnehmen. Ich kann meine Handlungen wiederholen und erfahre dadurch, dass sich die Gegenstände und Dinge in meiner Umgebung unterschiedlich anfühlen, dass sie unterschiedlich aussehen, riechen, schmecken, klingen usw.	Gestaltung des Nah- und Greiffelds: Bevorzugte Gegenstände, Materialien werden so angebracht, dass sie erreichbar sind und aktive Wiederholungen ermöglichen. Zeit für die selbsttätige Erkundung des Nah und Greiffeldes wird zur Verfügung gestellt. Empfohlen wird z.B. die Lagerung in Rückenlage auf einem Resonanzbrett, auf dem Materialien getastet werden können. Das Resonanzbrett verstärkt akustische Effekte und animiert zur Erkundung Im Stehständer werden Materialien im Greiffeld angebracht, die durch die aktiven Wiederholungen Spür-, Seh- und Höreindrücke auslösen und die Aufmerksamkeit anregen.
				1c	Welterkundung durch spezifisches Hantieren Spezifisches Hantieren erweitert die allgemein-mathematischen Kompetenzen durch die gezieltere aktiv-entdeckende Auseinandersetzung mit Dingen/Gegenständen und deren Funktion Inhaltsbezogene mathematische Vorerfahrungen Die Lernenden erkunden gezielt Dinge/Gegenstände und Materialien in ihrer unmittelbaren Umgebung und wenden als bewährt erfahrene Handlungsschemata (Lecken, Beißen, Klopfen, Werfen, Fallenlassen usw.) an. Auf diese Weise erfahren sie deren unterschiedlichen Eigenschaften (Vorerfahrungen für die Kompetenzbereiche GuM, ZuO), deren räumliche Anordnungen (Vorerfahrungen für die Kompetenzbereiche RuF) und die Veränderbarkeit von Mengen (Teile-Ganzes-Schema) (Vorerfahrungen für die Kompetenzbereiche ZuO). Die funktionsbezogene Nutzung ist noch nicht erschlossen. Als bewährt erfahrene Handlungsschemata werden auf Neues angewendet (Lecken, Beißen, Klopfen, Werfen, Fallenlassen usw.). Die Unterschiede in den Dingen/Gegenständen und Materialien, mit denen hantiert wird, führen zu neuen Erfahrungen.	Ich kann Materialien und Gegenstände mit dem Mund, den Augen und den Händen gezielter erkunden. Ich kann die dabei erprobten Handlungen (Lecken, Beißen, Fallenlassen…) zur Erkundung noch unbekannter Gegenstände anwenden. Ich kann beobachten, wie andere Menschen mit den Gegenständen umgehen und beginne dadurch wahrzunehmen, wie diese genutzt werden. Ich lerne, dass nicht alle meine erprobten Handlungsweisen für jeden Gegenstand geeignet sind. Ich beginne, Gegenstände durch bestimmte Merkmale als zueinander zugehörig wahrzunehmen.	Gestaltung des Handlungsfelds: Der Arbeitsbereich ist so zu gestalten, dass mit den darin erreichbaren Gegenständen hantiert werden kann (abgegrenzter räumlicher Bereich, Multifunktionstisch MFA-Tisch, Tastbretter, Materialkisten). Für das zunächst noch nicht an den Funktionen orientierte Erkunden durch Lecken, Beißen, Klopfen, Werfen usw. müssen Gegenstände und Materialien robust und stabil sein. Dadurch wird und ermöglicht, dass die unterschiedlichen Eigenschaften untersucht werden können. Materialkisten (ermöglichen Vorerfahrungen in den Bereichen GuM, ZuO) und verschiedene Behältnisse (ermöglichen Vorerfahrungen im Bereich RuF) werden zeitlich und räumlich verlässlich zur Verfügung gestellt (DuZ, RuF, MSufZ). Sie können ausgeleert und eingeräumt werden können. Mengen können umgefüllt, verändert und sortiert werden (Multifunktionstisch (MFA-Tisch n. Nielsen) (bedeutsam für die Kompetenzbereiche ZuO, MSufZ, RuF). Tastbretter mit daran befestigtem Material ermöglichen eine intensive Beschäftigung mit deren Eigenschaften (bedeutsam für die Kompetenzbereiche RuF, GuM, MSufZ).
					Allgemeine mathematische Vorerfahrungen (Beginn prozessbezogener Kompetenzen) Durch die Beobachtung anderer Menschen und im Dialog erfahren die Lernenden, dass die von ihnen gezeigten Handlungen gespiegelt und verbal begleitet werden. Die Nachahmungsfähigkeit wird so angebahnt und führt dazu, dass Gegenstände ihrer Funktion entsprechend genutzt werden. Eine unmittelbare Nachahmung ist damit noch nicht gesichert und entwickelt sich zunehmend.	Ich erlebe, dass es anderen Menschen wichtig ist, was ich tue, weil sie aufgreifen und nachmachen, was ich zeige. Ich schaue zu, wenn mir andere Menschen was vormachen und dazu sprechen. Das regt mich an, es nachzumachen.	Prozessbezogene Kompetenzen Bezugspersonen zeigen vorbildhaft die funktionsbezogene Nutzung von Gegenständen und regen zur Nachahmungsfähigkeit durch das Spiegeln gezeigter Handlungen an. Die sprachliche Begleitung unterstützt das Kommunizieren über konkret sichtbare Handlungen und Abläufe.
					Übergang zur elementaren Stufe: Mathematische Basiskompetenzen Vorzahlige Handlungen werden mit zahligem Handeln verbunden. Zahlwörter und Zahlen gewinnen im Alltag (zwei Äpfel, drei Brötchen), in Fingerspielen, Liedern und Geschichten und als Abbildungen sowie Mengenwissen (viel – wenig) an Bedeutung (bedeutsam für den Kompetenzbereich ZuO). Eigenschaften von Dingen werden verglichen (groß – klein, schwer – leicht, lang-kurz, kalt-heiß) (bedeutsam für den Kompetenzbereich GuM), räumliche und strukturierte Anordnungen (bedeutsam für den Kompetenzbereich MSufZ) dienen der Orientierung (oben-unten, hinten-vorne, aufgereiht, nebeneinander), die Gestalt der Dinge wird im Handeln erfahren (rund – eckig) (bedeutsam für den Kompetenzbereich RuF). Zeitliche Abläufe (erst – dann, gleich – später, Tage, Stunden, Minuten)) werden in sich wiederholenden Strukturen erfahren (bedeutsam auch für die Kompetenzbereiche GuM, DuZ, MSufZ).	Ich beginne, Zahlwörter und Zahlen im Alltag wahrzunehmen. Ich interessiere mich für Zahlen und Ziffern im Alltag, in Liedern und Geschichten. Ich handele mit Gegenständen in meiner Umgebung und beginne sie zu vergleichen und zu unterscheiden, ob sie groß oder klein, kurz oder lang, schwer oder leicht sind. Wenn ich mir eine Ansammlung von Gegenständen anschaue, kann ich einschätzen, ob es viel oder wenig Gegenstände sind. Ich kann sagen, wo sich die Dinge befinden (vorne, hinten…) und wie sie angeordnet sind (nebeneinander, übereinander usw.). Ich weiß, dass bestimmte Ereignisse jeden Tag, jede Woche zur gleichen Zeit stattfinden und kann darüber berichten. Ich habe eine Vorstellung dazu entwickelt, was es bedeutet, wenn ich einen Tag oder wenige Minuten auf etwas warten soll.	Inhalts- und prozessbezogene Kompetenzen Bezugspersonen thematisieren zahliges Handeln in Alltagszusammenhängen. Dabei werden die verschiedenen Bedeutungszusammenhänge bei der Verwendung von Zahlwörtern und Ziffern erklärt (Zahlen zum Abzählen, Zahlen zum Messen, Zahlen zum Bezeichnen (Haus-Nr., Auto-Nr.). Beispiele unter PIKAS Mathe ein Kinderspiel Literatur: (Koch u.a.2020) Die Lehrkraft beschreibt konkrete Handlungen im Alltag (bedeutsam für: GuM, DuZ, MSufZ) mit Mathematiksprache und regt zum Entdecken von mathematischen Handlungen an. Sie verwendet vorbildhaft Begriffe aus der Mathematiksprache (Darstellen, Kommunizieren): Zahlen, viel – wenig, mehr – wenige, um eins mehr, sind zusammen usw.
					Prozessbezogene Kompetenzen In Alltags- und Sachsituationen werden zur Klärung oder Problemlösung mathematische Beschreibungen wahrgenommen. Bei Mengenvergleiche werden Begriffe aus der Mathematiksprache gehört und angewendet (Darstellen und Kommunizieren ). Bei Reihenfolgen wird auf Ordnungszahlen Bezug genommen (1., 2., 3. sein). Strukturierte Darstellungen werden zur Orientierung angewendet.	Ich kann mich mit anderen darüber austauschen, ob alle gleich viel Dinge gesammelt haben oder nicht. Ich kann zeigen, woran ich das erkennen kann. Wenn wir einen Wettlauf machen, kann ich gemeinsam mit den anderen feststellen, wer 1., 2., oder 3. geworden ist.	Beispiele in: PIKAS: Fachwortschatz Mathematik
					Inhaltsbezogene Basiskompetenzen Beginn zahligen Handelns im Teilbereich Zahlen und Operationen Die Lernenden erleben, dass im Alltag Zahlwörter Anwendung finden und diese zur Orientierung (Raum-Nr., Telefon-Nr., Hausnummer usw.) und zum Vergleichen (Wer hat mehr – weniger?) genutzt werden können. Sie interessieren sich für Ziffern und Zahlwörter in ihrer Umgebung und werden in zahliges Handeln einbezogen. Die Lernenden beginnen, Zahlwörter und Ziffern unter verschiedenen Aspekten kennen zu lernen. Mengenwissen: Die Lernenden vergleichen und sortieren Gegenstände nach bestimmte Merkmalen. (groß-klein, schwer-leicht, usw.). Mengen werden im Spiel gebildet, verändert und verglichen. Wer hat mehr – weniger, gleich viel? Teile-Ganzes-Schema: Die Lernenden nehmen Gegenstände, Materialien auseinander, Mengen werden umgefüllt, in Teilmengen zerlegt. Eine ungezählte Menge kann in mehrere Behältnisse verteilt werden. Einzelne Teile oder Mengen werden an verschiedene Personen verteilt oder in verschiedene Behältnisse umgefüllt.	Ich weiß, dass Zahlen etwas bezeichnen können (Hausnummer, Telefonnummer, Raumnummer, Autonummer usw.). Wenn z.B. gesagt wird, dass wir uns im Raum 12 treffen, wissen alle ganz genau, welcher Raum gemeint ist. Ich kenne für mich wichtige Zahlen (Alter, Hausnummer, Anzahl von Körperteilen). Ich vergleiche Dinge und kann sie auf Grund ihrer unterschiedlichen Merkmale (Größe, Gewicht, Länge usw.) sortieren und ordnen. Ich kann erkennen (z.B. beim Tischdecken), wenn noch etwas fehlt (z.B. Löffel) oder ob zu viel da ist. Ich kann erkennen und sagen, wie viele Dinge noch gebraucht werden oder zurückgebracht werden müssen. Ich kann eine Menge von Gegenständen (z.B. Nüsse) in Teilmengen aufteilen (z.B. auf mehrere Teller). Ich kann alle Teilmengen wieder zusammenschütten.	Die Lehrkraft bezieht sich auf die verschiedenen Zahlaspekte bei der Verwendung von Zahlwörtern und verweist auf deren unterschiedliche Bedeutung: • Zahlwort steht für eine Menge (Kardinalzahlaspekt) • Zahlwort steht in einer geordneten Reihe (Ordinalzahl- und Ordnungsaspekt) • Zahlwort bezeichnet eine Größe (Maßzahlaspekt) (bedeutsam auch für den Kompetenzbereich GuM) • Zahlwort steht für eine Kennzeichnung(Codierungsaspekt). Datei „Zahlaspekte HO“ (bitte Link zur Datei erstellen) Materialkisten (Bausteine, Kastanien, Muggelsteine usw.) und Behältnisse stehen zur Verfügung und laden zum Umfüllen und Sortieren ein (bedeutsam auch für den Kompetenzbereich RuF). Alltagsgegenstände (Geschirr, Besteck, Behältnisse mit Deckeln usw.) werden weggeräumt und dabei sortiert (bedeutsam auch für die Kompetenzbereiche GuM, RuF).
					Zählstrategie/Zählprinzipien Die Lernenden erkennen die Zahlwortreihe als „unzerbrechliche Liste“ und sagen sie zunächst wie ein Gedicht auf. Sie lernen Zahlwörter kennen, wenn Dinge beim Aufsagen der Zahlwortreihe angetippt und „abgezählt“ werden. Die Reihenfolge wird noch verwechselt, Auslassungen (1,2,4,6) gehören dazu. Das Antippen und Abzählen (Eins-zu-Eins-Zuordnung) ist zunächst zufällig. Durch das Mitzählen und den Versuch des Abzählens erfahren die Lernenden, das die Zahlwortreihe gleichbleibt und dass bestimmte Zahlwörter zu bestimmten Mengen gehören.	Ich höre Zahlwörter im Alltag und in Geschichten, Liedern, Fingerspielen. Ich erfahre, dass Dinge durch die Zahlwortreihe abgezählt werden. Ich interessiere mich für das Mitzählen und versuche mitzuzählen. Ich sage die Zahlwortreihe wie ein Gedicht auf. Dabei verwechsle ich gelegentlich die Zahlenfolge oder lasse Zahlen aus Ich tippe beim Zählen auf die abzuzählenden Dinge. Manchmal tippe ich mehrmals auf dieselben Dinge oder überspringe einige.	Gelegenheiten im Alltag werden genutzt, um Mengen zu verändern, ergänzen, verringern, aufzuteilen. Zum spielerischen Erwerb der Zahlwortreihe und der Verwendung von Zahlworten werden Abzählreime- und Lieder angeboten. Alles kann gezählt werden und durch Abzählen können Mengen verglichen werden. Zum Mitzählen wird einladen. Es wird dargestellt und versprachlicht, dass die Zahlwortreihe gleichbleibt (Seriation, Ordinalzahlprinzip) und dass bestimmte Zahlwörter zu bestimmten Mengen gehören (Eindeutigkeitsprinzip).
					Anzahlkonzept: Die Lernenden interessieren sich für Zahlwörter und ordnen diese zunächst ohne Anzahlverständnis bestimmten Fingerbildern, Würfelbildern oder Ziffern (als Abbildungen) zu. Sie können Mengen durch die Stück-zu-Stück-Zuordnung (ohne Anzahlerfassung) vergleichen. Beim Abzählen steht die zuletzt genannte Zahl für die Anzahl (Menge). Die Stück-zu-Stück-Zuordnung wird mit dem Zählen (Anwendung der Zahlwortreihe) verbunden und kann zum Vergleichen von Mengen oder bei der Zerlegung von Mengen genutzt werden. Dies führt zur -> Eins-zu-Eins-Zuordnung	Das Abzählen gelingt mir aber immer besser. Ich beginne langsam zu verstehen, dass jedes Zahlwort zu einer ganz bestimmten Menge gehört. Ich erkenne einzelne Zahlen und nenne das Zahlwort dazu, ohne damit eine bestimmte Menge zu erfassen. Ich vergleiche Mengen, indem ich Dinge paarweise in einer Reihe anordne und erkenne, in welcher Reihe mehr oder weniger liegen oder ob es gleich viele sind. Ich erkläre, dass ich etwas dazutue oder wegnehme und dass sich dadurch die Menge verändert.	Beim Umfüllen, Aufräumen, Holen von Dingen usw. werden die Dinge mitgezählt.
					Prozessbezogene Kompetenzen Die Lernenden beginnen Sachsituationen mathematisch zu erfassen und zu erkennen, dass Fragen oder Probleme durch zahliges Handeln gelöst werden können. „Wie viel brauchen wir? Wie können wir feststellen, wer mehr oder weniger hat? Warum sortieren wir Dinge? Warum wird etwas verglichen?“ Über mathematisches Handeln wird kommuniziert und die Mathematiksprache kennengelernt. Die Darstellung von Anzahlen ist zunächst schematisch (Fingerbild). Die Verwendung von Zahlen beim Messen, beim Abwiegen oder zum Erkennen von zeitlichen Abläufen wird im Alltag thematisiert (bedeutsam auch für den Kompetenzbereich GuM).	Ich weiß, dass man mit Zahlen beschreiben kann, wieviel Dinge zu sehen sind und nenne Zahlwörter. Ich erkläre, dass ich etwas dazutue oder wegnehme und dass sich dadurch die Menge verändert. Auf die Frage „Wie alt bist du?“ kann ich ein Fingerbild zeigen Ich weiß, dass ich mit Zahlen eine Reihenfolge beschreiben kann (Erster, Zweiter, Dritter).	Prozessbezogene Kompetenzen Zahlwörter werden in konkreten Zusammenhängen und beim Vergleichen von Mengen und Veränderungen dargestellt und abgebildet (Ziffern, Fingerbilder, Würfelbilder). Zahliges Handeln wird auf diese Weise mit Mathematiksprache verbunden (kommuniziert) und vorbildhaft angeboten. „Wie viele Personen sind da und wie viele Teller benötigen wir?“ (Darstellen von realen Mengen z.B. durch die Übertragung auf Fingerbilder) Mathematische Modelle werden angeboten und die Beziehungen der Zahlen zueinander kommuniziert: „Wie viele, um wie viel mehr, wir tun dazu, wir nehmen weg?“ usw. (Gaidoschik 2007) Weitere Erklärungen: „Sprachgebrauch-Mathematikanfangsunterricht Hehn-Oldiges“ (Datei verlinken) PIKAS: Fachwortschatz Mathematik
					Zahliges Handeln auf konkreter Ebene Mengenwissen/Mengenbeziehungen: Die Lernenden bilden und verändern Mengen (Klassifizieren, Sortieren) und vergleichen sie durch Abzählen. Kleine Mengen (bis 4) und strukturierte Mengen (Finger – oder Würfelbilder) können simultan erfasst und benannt werden. Simultanerfassen und Quasisimultanerfassen bilden die Voraussetzung für das Bündeln (5er-, 10er-Bündel) Teile-Ganzes-Konzept/Zerlegungen Die Lernenden zerlegen konkrete zählbare Mengen vielfältig in Teilmengen (eine Menge von fünf Gegenständen/Dingen wird in Teilmengen zerlegt: z.B. in Einermenge und Vierermenge oder in Dreiermenge und Zweiermenge).	Ich kann kleine Mengen von Gegenständen (z.B. Knöpfe) verändern, indem ich noch welche dazulegen oder welche wegnehme. Durch Abzählen der so entstandenen Teilmengen kann ich diese vergleichen. Ich kann kleine Mengen bis Vier auf einen Blick erkennen und das Zahlwort dazu nennen.	Inhalts- und prozessbezogene Kompetenzen Im Alltag werden bestimmte Mengen beim Essen, Frühstück, Tisch decken, Kochen usw. benötigt. Diese werden benannt, zugeordnet, abgezählt, verglichen, zerlegt. Um Gesetzmäßigkeiten beim Erwerb des Anzahlverständnisses zu erwerben, verweisen Lehrkräfte auf Muster, Strukturen und funktionale Zusammenhänge (MSufZ).
					Zählstrategie/Zählprinzipien Die Lernenden beginnen beim Abzählen immer von der Eins an zu zählen („unflexible Zahlwortreihe“), um die Anzahl zu bestimmen. Dabei wird das Prinzip der stabilen Ordnung und das Eindeutigkeitsprinzip (Ordnungszahl/Ordinalzahlaspekt) erfasst. Mit der letztgenannten Zahl bezeichnen sie die Menge.	Ich kann eine Anzahl, die größer als Zwei ist, in verschiedene Teilmengen zerlegen. Ich erkenne Zahlwörter (im Alltag, in Geschichten, Liedern usw.) wieder und weiß, dass Dinge zählbar sind. Ich kann kleine Mengen von Dingen abzählen und so entscheiden, wo mehr und weniger sind. Ich weiß, dass ich Dinge abzählen kann, um Mengen zu verteilen und zu vergleichen. Wenn ich etwas abzähle, beginne ich immer mit der „Eins“. Das letztgenannte Zahlwort beim konkreten Abzählen nenne ich als Ergebnis. Ich erkenne Würfelbilder und kann das Zahlwort dazu nennen. Im Spiel zähle ich dann von der 1 bis zum gewünschten Zahlwort ab. Werden Finger- oder Würfelbilder anders angeordnet, beginne ich wieder von der Eins an zu zählen.	Beispiele PIKAS: Gute Aufgaben KIRA: Prozessbezogene Kompetenzen fördern Es werden im Alltag Gelegenheiten genutzt, kleine Mengen schnell zu erfassen (Gegenstände bis vier), zu ergänzen oder zu verringern. Unstrukturierte Mengen werden gezählt und strukturiert angeordnet. Arbeitsheft PIKAS: Vorschulische mathematikbezogene Grundkompetenzen Steinweg u.a. (2008) Mathe aktiv Brettspiele mit Würfelbildern und Figuren setzen. Das Zahlwort gibt an, wie viele Schritte gegangen werden darf. Es wird abgezählt. Die veranschaulichte Zahl z.B. auf dem Würfel wird in Handlung umgesetzt (Figuren setzen) und sprachlich begleitet. Zuordnen und Abzählen von Mengen, Ergebnisse vergleichen führt zur Lösung von Fragestellungen. Die Darstellung erfolgt noch konkret-anschaulich.
					Anzahlkonzept Die Lernenden nutzen die Eins-zu-Eins-Zuordnung zur konkreten Menge-Zahl-Zuordnung. Das Abzählen dient der Bestimmung der Anzahl: „Wie viele?“. Dabei werden Erfahrungen mit Invarianz (Anordnung der Dinge) und Repräsentanz (Größe der Dinge), die keinen Einfluss auf die Anzahl haben, gemacht. Das Nennen der letzten Zahl beinhaltet noch nicht sicher das kardinale Verständnis, sondern stellt die Vorstufe dazu dar: „(ab)zählendes Rechnen“ Lernende treffen in Alltagssituationen auf Zahlen, die Angaben über Maßeinheiten enthalten (Körpergröße, Maßangaben beim Kochen) (GuM).	Wenn ich Dinge abgezählt habe und gefragt werde, wie viele Dinge es sind, kann ich die Frage richtig beantworten, indem ich die letzte gesprochenen Zahl ansage. Wenn ich bis „Vier“ abgezählt habe, beginne ich zu verstehen, dass es vier Dinge sind. Ich weiß, dass mit Zahlen gemessen werden kann (z.B. meine Körpergröße oder Gewichte beim Kochen).	Die Darstellung von Finger- oder Würfelbildern wird verändert, um die Zerlegung und die Zahlbeziehungen zu verdeutlichen. Fingerbilder werden verändert, auch auf zwei Hände verteilt, um von der Abbildung zur Anzahl zu kommen. „Wie kann die vier noch gezeigt werden?“ Weitere Erklärungen: PDF-Datei „Finger- und Würfelbilder Hehn-Oldiges“ PDF-Datei „Würfelbilder und Anzahlverständnis Hehn-Oldiges“ Weitere Anregungen zum zahligen Handeln auf konkreter Ebene: PIKAS: Grundlagen sichern/Unterricht
					Prozessbezogene Kompetenzen Die Lernenden verwenden Zahlwörter im Alltag und das Abzählen konkreter Dinge zur Lösung von Fragestellungen gewinnt an Bedeutung. „Wie viele haben wir/benötigen wir?“ „Wie können alle gleich viel bekommen?“ Zur Problemlösung wird das Abzählen mit Hilfe der Zahlwortreihe genutzt. Die Lernenden erkennen, dass Anzahlen auf verschiedene Weise dargestellt werden können (Fingerbilder, Würfelbilder). Die Zerlegung von Teilmengen wird dargestellt und diese werden verglichen. Lösungswege werden kommuniziert.	Ich kann mit anderen darüber sprechen, wie viel wir von etwas haben, wie viel wir brauchen usw. Ich kann mit meinen Fingern oder am Würfel Zahlen zeigen und mit anderen darüber sprechen.	Prozessbezogene Kompetenzen Mathematische Handlungen werden durchgeführt, abgebildet und in Mathematiksprache beschrieben. Symbolische Darstellungen werden genutzt. Gemeinsam erstellte Wortspeicher beinhalten umgangssprachliche Redewendungen und Mathematiksprache (Modellieren, Kommunizieren). Vertiefung Fachsprache Mathematik (Goetze 2015)
					Zahliges Handeln auf ikonisch-anschaulicher Ebene Zahliges Handeln findet mit der Hilfe von Darstellungsmittel statt. Beginn innerer Vorstellungen Durch das Verwenden von Bündeln (5er- und 10er-Bündel) wird das Dezimalsystem veranschaulicht. Die Darstellung von 10er-Bündeln in Verbindung mit 100er-Tafeln und Mehrsystemblöcken zeigt die Beziehungen der Bündel im Dezimalsystem. Mengenwissen/Mengenbeziehungen Die Lernenden wissen, das Mengen aus Teilmengen bestehen. Das quasi-simultane Erfassen der Teilmengen durch Bündeln führt zu „schnellem Sehen“ (Kraft der 5 und Kraft der 10). Mengen werden verglichen und in Beziehung zueinander gesetzt. Mengen können durch Darstellungsmittel abgebildet werden. Teile-Ganzes-Konzept/Zerlegungen Die Lernenden zerlegen mit Darstellungsmitteln (Wendeplättchen) z.B. die Siebenermenge vielfältig z.B. in eine Dreier- und eine Vierermenge, in eine Zweier- und eine Fünfermenge und verändern sie (von der Siebenermenge werden zwei weggenommen, es bleibt eine Fünfermenge übrig usw.). Ziffern und Zahlwörter werden den abgebildeten Mengen zugeordnet und Zahlbeziehungen benannt.	Ich kann die Anzahl einer Menge von Dingen schnell erkennen, indem ich sie in Fünfer- oder 10er- Bündeln anordne. Dazu kann ich z.B. 10er, 20er-Felder nutzen. Ich kann eine Menge (z.B. von Wendeplättchen) durch Auseinanderschieben aufteilen. Ich kann die Menge wieder zusammenschieben und noch andere Aufteilungen erproben. Ich kann aus Mengen (z.B. 7 Wendeplättchen) in verschiedener Art und Weise Teilmengen bilden, ihnen jeweils eine Zahl zuordnen und ansagen durch welche Anzahl sich die Teilmengen unterscheiden. Wenn ich z. B. sieben Wendeplättchen in eine Zweier- und eine Fünfermenge aufteile, erkenne ich sofort,dass die Fünfermenge zwei Wendeplättchen mehr hat als die Zweiermenge.	Die Förderung auf dieser Stufe ist von besonderer Bedeutung, da sie im Förderschwerpunkt Lernen häufig wenig Berücksichtigung findet und das „Abzählen“ (auch in Lehrwerken) als „zählendes Rechnen“ akzeptiert wird. Die Lernenden benötigen zu dessen Überwindung die hier zu entwickelnden Kompetenzen. Zum Aufbau des Bündelns werden Übungen zum schnellen Erkennen von Mengen angeboten. Die Bedeutung des strukturierten Erfassens von Anzahlen wird durch vielfältige Übungen erfasst. Beispiele unter: PIKAS: Schnell sehen Darstellungsmittel bieten 10er-Strukturen an, um das Dezimalsystem zu veranschaulichen und auf das Stellenwertsystem hinzuführen. 10er-, 20er, 100erfelder, Würfelmaterial (Mehrsystemblöcke) Einer, Zehnerstangen, 100er-Felder usw.
					Zählstrategie/Zählprinzipien Die Lernenden zählen von einer beliebigen Zahl aus weiter und wenden so die „teilweise flexible Zahlwortreihe“ (Weiterzählen) an. Es beinhaltet das Verstehen des Ordinalzahlprinzips und des Prinzips der Irrelevanz der Anordnung. Zahlen bilden eine Ordnung ab, die Zählzahl hat eine feste Stelle in der Zahlwortreihe, es gibt feste Vorgänger und Nachfolger. Die Rangzahl (Ordnungszahlaspekt) gibt den Rang an (der/die Wievielte?).	Ich kann beim Abzählen von einer beliebigen Zahl aus weiterzählen. Ich weiß, dass jede Zahl in der Zahlwortreihe einen festen Platz hat. Jede Zahl hat genau eine Vorgängerzahl und genau eine Nachfolgerzahl. Ich kann mit Hilfe von Zahlwörtern ansagen, in welcher Reihenfolge wir beim Wettlauf angekommen sind. Ich kann also sagen, wer der Erste, der Zweite, der Dritte usw. war.	PIKAS: Zahlverständnis im Anfangsunterricht Lehrkräfte analysieren die Lehr- und Übungsformate von Lehrwerken, Spielen und Materialien: Inwieweit werden Beziehungen zwischen Anzahlen, Bündelungen, Zerlegungen usw. zugrunde gelegt und durch Übungen erfahrbar gemacht. Werden „schöne Päckchen“ genutzt usw. Um das Verstännis für die Zahl Null zu ermöglichen, werden Mengen (Bausteine, Stifte usw) soweit reduziert, bis kein Element mehr vorhanden ist. Diese Situation stellen die Lernenden als Minusaufgabe mit dem Ergebnis 0 dar. PDF-Datei „Kriterien Lehrmittel Mathematik Hehn-Oldiges“ PDF-Datei „Darstellungsmittel im Mathematikunterricht Hehn-Oldiges“ Royar (2016): Wenn Vereinfachung zur Verfälschung wird
					Anzahlkonzept Die Lernenden erfassen die Menge als Anzahl (Loslösung vom (ab)zählenden Rechnen) und zerlegen sie vielfältig (7 = 2 + 2 +3 oder 4 + 3). Das Kardinalzahlprinzip beinhaltet das Verständnis, dass die Zahl für eine bestimmte Menge steht (Mächtigkeit).. Eine Menge ohne Elemente wird mit der Zahl Null bezeichnet. Zahlwörter stehen für Mengen und anhand der Zahlen können diese verglichen und in Beziehung gesetzt werden. Anzahlen und Operationen werden strukturiert erfasst und mit Material visualisiert (Darstellungsmittel).	Ich weiß, dass jede Zahl für eine bestimmte Menge steht. Dabei ist es ganz egal, welche Dinge eine Menge bilden. Z.B: kann ich ansagen, wie viele Kinder am Tisch sitzen, in wie vielen Tagen ich Geburtstag habe oder wie viele Gegenstände in meiner Hosentasche versteckt sind. Ich kann solange Dinge wegnehmen, bis keines mehr übrig ist und sagen, dass es 0 sind.	Bildliche Darstellungen in Lehrwerken sind für Lernende nicht immer eindeutig für die Aufgabenumsetzung. Lehrkräfte tauschen sich daher mit Lernenden über unterschiedliche Deutungen aus. KIRA: Bildliche Darstellungen Wittmann/Müller (o.J.) Blitzrechnen
					Prozessbezogene Kompetenzen Die Lernenden stellen und lösen Aufgaben wie: Wie können wir eine bestimmte Anzahl darstellen? Wie können wir eine Anzahl schnell erkennen? Die Lernenden entwickeln tragfähige Grundvorstellungen, wenn eine Aufgabe in eine mathematische Handlung an Material, in ein Bild oder eine Rechengeschichte übertragen wird, bzw. eine Handlung, ein Bild oder eine Rechengeschichte in eine Aufgabe übersetzt wird. Die Lernenden modellieren Additions- und Subtraktionsaufgaben zu Situationen und entwickeln aus Situationen Aufgaben. Die Lernenden modellieren individuell ihre Lösungswege und argumentieren in 2er- oder Gruppensettings unter Anwendung der genutzten Darstellungsmittel. Die unterschiedlichen Lösungswege werden verglichen und es wird darüber kommuniziert.	Ich kann bestimmte Anzahlen mit Hilfe von Wendeplättchen so darstellen, dass die Anzahl ganz schnell, am besten ohne Zählen erschlossen werden kann. Das gelingt mir zum Beispiel, wenn ich mich an den Würfelbildern orientiere. Ich kann eine bestimmte Anzahl mit Plättchen darstellen und nutze dazu 10er, 20er oder 100erfelder. Ich kann beschreiben, wie ich eine Anzahl in Teilmengen zerlege und daraus eine Plusaufgabe oder eine Minusaufgabe abbilde.	Prozessbezogene Kompetenzen Lehrkräfte unterstützen den Erwerb von Grundvorstellungen. Konkrete Anregungen unter PIKAS: „Mathe in den Kopf“ Der Wortspeicher mit Alltags- und Mathematiksprache wird bei der Einführung von Darstellungsmitteln erweitert, um mathematische Handlungen darstellen und kommunizieren zu können. Lehrkräfte organisieren und begleiten Rechenkonferenzen: Lernende stellen im Anschluss an die individuelle Bearbeitung einer Aufgabe ihre Lösungswege und Ergebnisse der Gruppe vor. Dort werden die Lösungen dargestellt, kommuniziert, verglichen und reflektiert. Lehrkräfte erhalten dabei einen differenzierten Einblick in die Kompetenzen der Lernenden. PIKAS: Mathe-Konferenzen
					Handeln auf mental-konkreter Ebene Lernende lösen sich zunehmend von konkreten Handlungen und entwickeln mentale Vorstellungen, die auf entfalteten Grundvorstellungen für das Operationsverständnis von Addition und Subtraktion basieren.	Ich kann Plusaufgaben sicher lösen und Rechengeschichten des Dazulegens, Draufpackens, Dazuzeichnens, des Vermehrens usw. dazu erfinden. Ich kann Minusaufgaben sicher lösen und Rechengeschichten des Wegnehmens, Aufessens, Durchstreichens usw. dazu erfinden.	Lehrkräfte bieten vielfach Materialien und Aufgabenformate an, die den Aufbau mentaler Vorstellungen ermöglichen. Zur Entwicklung des Operationsverständnisses können Materialien des DZLM genutzt werden. DZLM: Mathe sicher können
					Grundvorstellungen: Zählstrategie: Nutzung der „flexiblen Zahlwortreihe“ Lernende erkennen, dass das Zählen von der größeren Anzahl aus, eine einfachere Strategie darstellt. Es wird verstanden, dass ein Zahlwort Anzahlen enthält, von denen für die Addition weitergezählt werden kann, um die Gesamtzahl zu erhalten (Die Aufgabe 3 + 5 wird vereinfacht gelöst, indem von der größeren Zahl 5 aus um 3 Schritte weitergezählt wird: 6, 7, 8, d.h. 5 + 3 = 8). Das Kardinalzahlprinzip ist erworben und das „Abzählen“ kann so überwunden werden. Lernende entwickeln innere Vorstellungen. Zählbare Teilmengen sind vorstellbar, auch wenn sie nicht sichtbar sind.	Ich weiß, dass eine Zahl einen bestimmten Platz in der Zahlwortreihe hat. Ich weiß, dass es einfacher ist, bei einer Plusaufgabe von der größeren Zahl aus zu zählen. Ich kann mir verdeckte Teilmengen vorstellen und überprüfen, ob meine Lösung stimmt.	Lehrkräfte ermitteln die bisher erreichten mathematischen Fähigkeiten, um die individuelle Förderung gestalten zu können. Anregungen in: PIKAS - Standortbestimmung FÖDIMA (2024): Diagnostizieren und Fördern Lehrkräfte bieten vielfach Materialien und Aufgabenformate an, die den Aufbau mentaler Vorstellungen ermöglichen. Ausführliche Darstellung und konkrete Übungsangebote: PIKAS Grundlagen sichern/Hintergrund PIKAS: Sicher im 1+1 MAHIKO: Sicher im 1plus1 PIKAS: Rechenschwierigkeiten vermeiden PIKAS Materialien nichtzählendes Rechnen 1 + 1 und 1 – 1 (TaskCard) Konzeptuelles Wissen unterstützen (z.B. Zeindl-Steiner 2012)
					Vorgänger- und Nachfolgerzahlen: Lernende nutzen die Beziehung zwischen den Zahlen: immer um eins mehr oder um eins weniger. Die Zahl fünf kann auf dem Zahlenstrahl für die Abschnitte 1, 2, 3, 4, 5 oder 7, 8, 9, 10, 11 stehen.	Ich weiß, dass in der Zahlenreihe die Zahl Vorgänger- und Nachfolgerzahlen hat, die immer um eins mehr oder ein weniger als sie selbst sind.
					Quasi-simultanes Erfassen: Lernenden wird das Erfassen großer Anzahlen durch Bündelungen ermöglicht (Blitzblick, Strichlisten) und damit das kardinale Verständnis gesichert. Das strukturierte Erfassen von Zahlenwerten (Einer, Fünfer, Zehner) fördert die Einsicht der Lernenden in das Zehnersystem (Dezimalsystem) und stellt die Basis für das Stellenwertverständnis dar.	Ich kann große Zahlen erkennen, wenn sie gebündelt sind: 10er, 20er, 100erfelder, Strichlisten usw. Ich weiß, dass es einfach ist, mit Fünfern und Zehnern zu rechnen und kenne Darstellungsmittel, die mir dabei helfen.
					Anzahlverständnis und Operationsverständnis Lernende nutzen das Anzahlverständnis. Zahlen stehen in Beziehungen zueinander. (An)Zahlen beinhalten andere (An)zahlen: die Zahl fünf kann den Teil einer Menge (Anzahl) oder die Anzahl der Gesamtmenge darstellen (relationale Differenzen). Anzahlen werden zerlegt und verglichen. Lernende verstehen, dass die Grundaufgaben der Addition auf dem Hinzufügen und dem Vereinigen von Mengen basieren und Grundaufgaben der Subtraktion auf dem Wegnehmen (Abziehen) und Ergänzen basieren. Lernende verstehen die Grundaufgaben der Addition (Einspluseins) und der Subtraktion (Einsminuseins) in ihren Beziehungen untereinander und wenden Umkehroperationen an.	Ich kenne Darstellungsmittel und weiß, wie ich damit Plus- und Minusaufgaben rechnen kann. Ich kann mit Darstellungsmitteln Anzahlen zerlegen. Ich kann Mengen vergrößern, indem ich zu einer Teilmenge eine andere Teilmenge hinzufüge . Die Gesamtmenge kann ich durch eine Plusaufgabe ausrechnen.
					Konzeptuelles Wissen basiert auf dem Verständnis: Lernende wissen, dass eine Zahl (Ziffer/Zahlwort) einen bestimmten Platz in der Zahlwortreihe hat. Eine Zahl steht für eine Anzahl, die zerlegt werden kann (Sieben ist das Gleiche wie 3+4 oder 2+5 oder 1+6). Die Zahl kann durch Darstellungsmittel (Anzahl der Finger, Plättchen, Striche) abgebildet werden. Eine bestimmte Zahl steht in Beziehung zu anderen Zahlen (Sieben ist eins mehr als sechs, eins weniger als acht, zwei mehr als fünf und drei weniger als zehn)(vgl. Zeindl-Steiner 2012)	Ich kann Mengen verkleinern, indem ich von der Gesamtmenge etwas wegnehme. Die Restmenge kann ich durch eine Minusaufgabe ausrechnen. Ich weiß, wie eine Minusaufgabe in eine Plusaufgabe oder eine eine Plus- in eine Minusaufgabe umgekehrt werden kann. Ich weiß, dass eine Zahl für eine bestimmte Menge steht, die zerlegt werden kann und so Plus oder Minusaufgaben entstehen.
					Prozessbezogene Kompetenzen Lernende nutzen unterschiedliche Darstellungsmittel (z.B. Würfelmaterial – Mehrsystemblöcke, Plättchen, Strichlisten, Zahlenstrahl usw.), um ihre Lösungswege zu erkläre (darstellen, argumentieren). Sie bilden konkrete Handlungen und mathematische Handlungen in unterschiedlicher Weise ab. Sie kommunizieren auf diese Weise anderen Lernenden ihre Lösungswege, begründen ihre Darstellungen und vergleichen ihre Wege und Ergebnisse in der Gruppe. Die Vernetzung der Darstellungen (Sprache, symbolische Darstellung durch Ziffern und Operationszeichen, Zeichnungen usw.) führen zum abstrakten Zahlenrechnen. Es kann zwischen verschiedenen Darstellungsformen gewechselt werden. Die Handlungen können in Rechengeschichten übertragen werden oder eine Rechengeschichte wird abgebildet. Rechengeschichten Sachaufgaben und Rechengeschichten stellen die Verbindung zur Anwendung mathematischen Handelns dar. Sachrechenanlässe und realitätsbezogenen Aufgaben dienen der Umwelterschließung (Verbindung zu den Kompetenzbereichen GuM, RuF, DuZ). Lernende entwickeln eigene Rechengeschichten, die mathematische Lösungswege erfordern oder können aus Rechengeschichten Plus- oder Minusaufgaben ableiten.	Ich kann Darstellungsmittel nutzen, um Aufgaben darzustellen und zu zu lösen. Ich kann erklären, wie ich Zahlen als Fingerbild oder durch Plättchen und Striche zeigen oder darstellen kann. Ich kann zeigen und erklären, dass eine Zahl eine kleinere oder größere Anzahl als eine andere Zahl beinhaltet. Ich kann anderen erklären, wie ich rechne und zeige, welche Darstellungsmittel mir dabei helfen. . Ich kann mir zu Plus- und Minusaufgaben Rechengeschichten ausdenken. Ich entdecke in Vorgängen des Dazulegens oder Wegnehmens, in entsprechenden Rechengeschichten oder Abbildungen, die dort versteckten Plus- oder Minusaufgaben und schreibe sie auf.	Prozessbezogene Kompetenzen Die Methode „Rechenkonferenz“ ermöglicht einer Gruppe von Lernenden, ihre individuellen Lösungswege darzustellen, zu vergleichen (argumentieren) und gemeinsam zu reflektieren (kommunizieren). Es werden vorbildhaft verschiedene Strategien weitergegeben, durch die das Ablösen vom Abzählen überwunden werden kann. Rechenwege werden gefestigt, wenn sie von den Lernenden selbst erklärt und beschrieben werden können (argumentieren) . Besonders im Austausch über verschiedene Lösungswege für den Zehnerübergang wird deutlich, dass der „Zehnerstopp“ nur eine Möglichkeit darstellt. Die Ablösung vom Abzählen wird so erleichtert. PIKAS: Mathe-Konferenzen Lehrkräfte nutzen Alltagszusammenhänge, um daraus Rechenanlässe abzuleiten und zu diskutieren (Verbindung zu den Kompetenzbereichen GuM, DuZ, RuF). PIKAS: Rechengeschichten KIRA Beispiele Rechengeschichten
					Zehnerübergang Lernende können verschiedene Strategien beim Rechnen mit Zehnerübergang entwickeln, wenn sie die Beziehungen zwischen Anzahlen und deren Zerlegungen verstanden haben und ein Verständnis für das Stellenwertsystem vorliegt. Wird der sogenannte „Zehnerstopp“ als einzige alternativlose Strategie angeboten, werden andere Strategien nicht erkannt. Stellenwertverständnis Lernende nutzen zunächst Zerlegungen und Operationen im Zahlenraum bis 20, um Sicherheit darin zu erlangen. Gleichzeitig können aber bereits Darstellungsmittel im Zahlenraum bis 100 angeboten werden, um eine Vorstellung des Dezimalsystems anzuregen. Das Stellenwertverständnis basiert auf der Erkenntnis, dass jeweils zehn Objekte mit dem Zahlenwert Einer (zehn Einer) zu einem Bündel höherer Ordnung (Zehner) zusammengefasst werden. Jeweils zehn Objekte können mit dem Zahlenwert Zehner zu einem Bündel höherer Ordnung zusammengefasst (ein Zehner, zwei Zehner usw.) und wieder entbündelt werden. Die Lernenden gewinnen so, zunächst im Zahlenraum 100, Einsicht in das dezimale Bündelungsprinzip.	Ich kann auf unterschiedlichen Wegen und mit unterschiedlichen Darstellungsmitteln Aufgaben rechnen, die über den Zehner gehen. Ich weiß, dass ich jeweils 10 Objekte (Zahlenwert „Einer“) zu einem Bündel zusammenfassen kann verwende dazu den Zahlenwert „Zehner“. Ich bündle 12 Einer in einen Zehner und 2 Einer. Ich weiß, dass ich die Bündel wieder in einzelne Teile zerlegen kann (Zehner in Einer).Ich entbündele einen Zehner in 10 Einer. Ich weiß, dass ich 10 Zehner zu einem Hunderter bündeln kann. Ich weiß, dass die erste Ziffer einer zweistelligen Zahl für die Anzahl der Zehnerbündel steht und die zweite Ziffer für die Einer. Das heißt, dass z. B. bei der Zahl 23 die erste Ziffer (2) für die Zehnerbündel und die zweite Ziffer (3) für die Einer steht. Die Zahl 23 lässt sich also in 2 Zehner und 3 Einer entbündeln.	Der Zehnerübergang begründet sich in der Struktur des Zehnersystems (Dezimalsystems), die den Lernenden durch das Stellenwertsystem verdeutlicht wird. Lehrkräfte benötigen umfassende Kenntnisse zu den unterschiedlichen nichtzählenden Rechenstrategien, um die Lernenden beim Zehnerübergang unterstützen zu können. s. zB. Apfler, S (o.J.).: Flexibles Rechnen beim Zehnerübergang: Der Zehnerstopp (schrittweise Rechnen bis zur 10) als einzige Strategie verhindert, dass Lernende unterschiedliche Rechenstrategien nutzen, die für das abstrakt-symbolische Rechnen notwendig sind. Lehrwerke sind daraufhin zu überprüfen. Gaidoschik, M. (2012): Viele Wege führen über den Zehner Um ein tragfähiges Stellenwertverständnis zu erreichen, müssen die Lernenden dabei unterstützt werden, den Aufbau unseres Zahlsystems zu verinnerlichen. Dazu gehört die Einsicht in das dezimale Bündelungsprinzip, dass mit Hilfe geeigneter Darstellungsmittel erarbeitet wird. Übungsangebote in: PIKAS: Aufbau eines tragfähigen Stellenwertverständnisses DZLM: Wortspeicher zum Bündeln und Zehnersystem
					Übergang zur abstrakt-symbolischen Ebene Rechenoperationen finden auf der rein symbolischen Ebene statt. Gesamtmenge und Teilmengen sind gedanklich vorstellbar. Die nichtzählende Rechenstrategie basiert auf der „vollständig flexiblen Zahlwortreihe“. Zahl und Zahlwort symbolisieren Anzahlen. Das Abzählen als alleinige Rechenstrategie ist überwunden. Sind die nichtzählenden (heuristische) Strategien erworben, kann das „Kleine 1+1“ anhand der Einspluseinstafel erfasst und zum Abrufen der Aufgaben gespeichert werden. Dazu werden Kernaufgaben genutzt: • Kernaufgaben (einprägsame Aufgaben) - Aufgaben mit dem Summanden 0, 1, 5 und 10 - Verdoppelungsaufgaben - Aufgaben zur Zerlegung der 10 - Nachbaraufgaben, Tauschaufgaben • Nachbaraufgaben (zu jeder Vergrößerung bzw. Verkleinerung eine Summanden um 1 kann die jeweilige Nachbaraufgabe gebildet werden) • Verdoppelungsaufgaben (prägen sich leicht ein) 6+6= 12. 6+7 = 12 +1 (Nachbaraufgabe) • Tauschaufgaben (Kommutativgesetz) Das relationale Zahlverständnis zeigt sich z.B. in der Anwendung von Tauschaufgaben (Kommutativgesetz): 7 = 3+4, 7=4+3, 7-4=3, 7-3=4 oder Zerlegungsstrategien 7=3+2+2= 5+2 usw. und beim Verstehen der Umkehrbarkeit von Aufgaben: A+?=C 3+?=8 ?+B=C ?+5=8 ?-B=A ?-5=3 • Umkehraufgaben: Die Lösung der Subtraktionsaufgabe 17 - 9 wird durch Rückgriff auf die Additionsaufgabe 8 + 9 = 17 gefunden. Gleichsinniges oder gegensinniges Verändern Gegensinniges Verändern: Durch Verkleinerung des ersten Summanden und gleichzeitige Vergrößerung des zweiten Summanden um dieselbe Zahl bleibt eine Summe unverändert: 5 + 3 wird über 4 + 4 gelöst. Gleichsinniges Verändern: Eine Differenz bleibt unverändert, wenn wir Minuend und Subtrahend um denselben Betrag vergrößern oder verkleinern: 12 - 9 wird über 13 - 10 gelöst. Halbschriftliches Rechnen: Aufgaben werden in leichte Teilaufgaben zerlegt und die Rechenschritte werden notiert. Zuletzt wird das Ergebnis notiert. Strategien: Stellenweise: Beide Summanden werden in Stellenwerte (Zehner -Z und Einer-E) zerlegt und anschließend die Gesamtsumme ermittelt (Z + Z, dann E + E oder E + E, dann Z + Z) Schrittweise: Ein Summand wird in seine Stellenwerte zerlegt (ZE + Z dann +E oder ZE + E dann +Z) Vereinfachen durch gegensinniges oder gleichsinniges Verändern.	Ich weiß, dass Zahlen und Zahlwörter für eine Anzahl stehen und kann Aufgaben ohne Darstellungsmittel im Kopf lösen. Ich kann Plus- und Minusaufgaben schriftlich lösen. Ich kann die Zahl 10 unterschiedlich zerlegen und daraus Plus- und Minusaufgaben bilden. Ich kann mir Aufgaben mit den Summanden 0.1.5 und 10 gut merken. Ich nutze Nachbaraufgaben, um eine Aufgabe zu lösen. Ich kann mir Verdoppelungsaufgaben gut merken und wende sie zur Lösung von Aufgaben an. Ich weiß, dass ich die Summanden einer Plusaufgabe vertauschen und auch zerlegen kann. Dieses Wissen nutze ich, um mir das Rechnen zu erleichtern. Ich weiß, dass ich Minusaufgaben in Plusaufgaben und Plusaufgaben in Minusaufgaben umkehren kann. Ich kann Aufgaben, bei denen eine Zahl fehlt, ausrechnen, weil ich weiß, wie ich bei Plusaufgaben mit fehlender Zahl eine Minusaufgabe oder bei Minusaufgaben eine Plusaufgabe bilden kann. Ich kann eine Minusaufgabe lösen, wenn ich die passende Plusaufgabe kenne. Ich kann durch Verkleinern und Vergrößern eine Aufgabe für mich einfacher machen. Ich kann Aufgaben in für mich leichte Teilaufgaben zerlegen, und die Schritte aufschreiben und so das Gesamtergebnis ermitteln.	Auf der Grundlage des Wissens um Beziehungen zwischen Zahlen (relationales Zahlenverständnis) kann das 1+1 durch „produktives Üben“ für das schnelle Abrufen gespeichert werden. PIKAS Einspluseinstafel PIKAS 1plus1 richtig üben Übungsformate Die Auswahl an Aufgaben ermögliche, inhaltsbezogene und prozessbezogene Kompetenzen zu fördern. Im Gegensatz zu häufig in Lehrwerken vorkommenden reine klassische „Ausrechenpäckchen“ werden „schöne Päckchen“ angeboten, die ermöglichen, sich mit Zahlbeziehungen und mathematischen Gesetzmäßigkeiten auseinanderzusetzen (SfuZ). KIRA: schöne Päckchen Lehrkräfte bieten nichtzählende (heuristische) Strategien an, diskutieren sie mit den Lernenden und ermöglicht die Ablösung vom Abzählen. Für Mathekonferenzen werden Wortspeicher erarbeitet. Halbschriftliches Rechnen ermöglicht der Lehrkraft, die gedanklichen Schritte der Lernenden nachvollziehen zu können und diagnostisch zu ermitteln, an welcher Stelle es zu Verständnisfehlern kommt. Beispiele: KIRA: Halbschriftliche Addition PIKAS: Halbschriftliche Addition
					Prozessbezogene Kompetenzen Die Lernenden nutzen abstrakt-symbolische Operationen, um mathematische Handlungen abzubilden. Sie übertragen Fragestellungen auf die rein symbolische Ebene (Modellieren) und können aus abstrakten Aufgaben Rechengeschichten erfinden. Lernende finden bei Fragestellungen/Problemen und in Sachfragen relevante Informationen, die sie zu mathematischen Lösungswegen führen. Diese werden erprobt, indem Einsichten in Operationen genutzt werden (Problemlösen). Mathematische Zusammenhänge werden vermutet und überprüft. Dazu werden die Lösungswege dargestellt (Argumentieren, Darstellen, Kommunizieren).	Ich kann mir aus Aufgaben Rechengeschichten ausdenken oder aus Rechengeschichten Aufgaben erstellen. Ich kann Textaufgaben in Einzelaussagen zerlegen, diese veranschaulichen und überlegen, welche der Angaben für das Entdecken der gesuchten Aufgabe wirklich wichtig sein könnten. Ich frage, was gegeben und was gesucht wird, ob es sich in der Beschreibung um Dazulegen/Vergrößern oder Wegnehmen/Verkleinern handelt. Wenn ich diese Fragen alle gut durchdacht habe, kann ich eine Rechenaufgabe erschließen. Ich muss noch mal prüfen, ob ich alles gut durchdacht habe und meine Entscheidung für den Lösungsweg begründen.	Prozessbezogene Kompetenzen Lernende werden angeregt, sich über Aufgabenpäckchen auszutauschen (kommunizieren) und selbst Päckchen zu erfinden (modellieren), die einer von ihnen erdachten Logik folgen. KIRA: Schöne Päckchen Lehrkräfte bieten für das Mathematisieren von Situationen (Sachaufgaben/Textaufgaben) mathematische Modelle an (MSfuZ). Die Modelle werden auf die Fragestellung aus der Situation angewendet, interpretiert und überprüft. Grundlagenliteratur (Franke/Ruwisch 2010): Worauf beim Sachrechnen zu achten ist? Wittmann u.a. (o.J.) Offene Sachaufgaben
					Multiplikation und Division		Im Folgenden werden die prozessbezogenen Kompetenzen mit den inhaltsbezogenen Kompetenzen zusammen dargestellt.
					Voraussetzung für den Erwerb der Multiplikation und Division ist das abstrakt-symbolische Anzahlverständnis im zweistelligen Zahlenraum. Zunächst wird das Verständnis für die Multiplikation gesichert. Erst dann folgt die Umkehr in Division (Gaidoschik, 2017). Grundvorstellungen Multiplikation Bei der Multiplikation handelt es sich um eine Zusammenfassung vervielfachter Additionen und dient der Vereinfachung von Rechenoperationen. D.h. es wird das Wissen um die mathematische Gleichwertigkeit einer vervielfachten Addition wie z.B. 4+4+4 mit der entsprechenden Multiplikation 3 mal 4 aufgebaut. Vervielfachte Additionen können sich in verschiedenen Kontexten ergeben. Die Lernenden entwickeln ein umfassendes Verständnis zur Operation der Multiplikation, das es ihnen ermöglicht, Multiplikationsaufgaben in verschiedenen Kontexten zu deuten/erkennen und die Aufgaben zueinander in Beziehung zu setzen. (ausführliche Erläuterung in MAHIKO Multiplikation verstehen - Grundlagen Ein umfassendes Verständnis der Multiplikation (KIRA Operationsverständnis Multiplikation) basiert erstens auf mentalen Bildern (Vorstellungen), die die Lernenden jeweils im Sinne der Multiplikation deuten können. Für das Verständnis sind folgende Bilder notwendig: -Die Vorstellung von Situationen der Wiederholung von Tätigkeiten gleichen Umfangs, -die Vorstellung von Situationen des Zusammenfassens (gleichgroße Anzahlen werden gruppiert und deren Gesamtzahl wird ermittelt) sowie - die Vorstellung von Situationen des Vergleichs zwischen Anzahlen und Größen, die multiplikativ zueinander in Beziehung gesetzt werden.	Ich kann in Erzählungen oder Beobachtungen in Handlungen, die mehrfach in gleicher Art und Weise ausgeführt werden, eine Malaufgabe entdecken. Wenn ich zum Beispiel beobachte, dass Tina dreimal zum Plätzchenteller geht und immer zwei Plätzchen mitbringt, dann entdecke ich in dieser Geschichte die Malaufgabe 3•2, die ich ausrechnen kann. Ich weiß, dass ich auch zum Ergebnis komme, wenn ich aus der Malaufgabe eine Plusaufgabe mache und 2+2+2 rechne. Ich entdecke Malaufgaben in meiner Umgebung oder auf Bildern, wenn Anzahlen gleicher Größe sortiert angeordnet sind. Zum Beispiel kann ich beim Betrachten eine Kiste mit 4 Reihen und jeweils 3 Flaschen, die Aufgabe 4•3 entdecken, die ich ausrechnen kann. Ich weiß, dass ich auch zum Ergebnis komme, wenn ich aus der Malaufgabe eine Plusaufgabe mache. Ich kann auch Malaufgaben nutzen, um Anzahlen und Größen zu vergleichen. Wenn mir zum Beispiel gesagt wird, dass Tina 6 Plätzchen hat und Tom doppelt so viele, dann entdecke ich die Malaufgabe 6•2 und rechne aus, dass Tom 12 Plätzchen hat. Ich weiß, dass ich auch zum Ergebnis komme, wenn ich aus der Malaufgabe eine Plusaufgabe mache.	Das Erlernen der Multiplikation darf nicht darauf beschränkt werden, dass Lernende die Aufgaben des kleinen Einmaleins auswendig lernen und automatisiert wiedergegeben werden können (s. Gaidoschik, 2009) Die Fähigkeit, Malaufgaben flexibel und sicher zu lösen, ist vielmehr auf ein umfassendes Verständnis der Multiplikation angewiesen. Deshalb sollte der Lernprozess darauf ausgerichtet sein, dieses Verständnis zu ermöglichen und zu festigen (Gaidoschik 2017). Die folgenden 4 Aufgabentypen sind ausführlich beschrieben unter: MAHIKO: Multiplikation verstehen - Übungen (1)Malaufgaben in der unmittelbaren Umgebung suchen Die Lernenden werden aufgefordert, Malaufgaben im Klassenraum, auf dem Schulhof, im Supermarkt, auf der Straße … zu suchen, diese zu skizzieren oder zu fotografieren ( z.B. gruppenweise angeordnete Türschilder, Fenster, gestapelte Kisten usw.). Die gesammelten Bilder werden in der Gruppe unter dem Aspekt der Multiplikation diskutiert, als Abbildung schematisiert und als Malaufgabe formuliert. (2)Malaufgaben auf dem Hunderterpunktefeld markieren Malaufgaben werden flächig auf dem Hunderterpunktefeld mithilfe eines sogenannten Malwinkels dargestellt, farbig markiert, diskutiert und als Malaufgabe formuliert. (3)Malaufgaben auf dem Zahlenstrahl veranschaulichen Unterschiedliche Malaufgaben werden vorgegeben und in der Lerngruppe verteilt. Die Lernenden stellen „ihre Aufgabe“ durch „Sprünge“ auf dem Zahlenstrahl dar. Anschließend deuten die Lernenden gegenseitig die Darstellungen als Malaufgaben und ermitteln die Ergebnisse. (4)Übungen zur Verknüpfung verschiedener Darstellungsformen: Was passt? Alltagsbilder, didaktische Bilder, Rechengeschichten und Rechenaufgaben werden vorgegeben (Spielkarten können von Kindern auch selbst erstellt werden), von den Lernenden hinsichtlich der Multiplikation gedeutet, diskutiert und passend geordnet.
					Prozessbezogene Kompetenzen Das umfassende Verständnis der Multiplikation ist zweitens mit der Fähigkeit der Lernenden verknüpft, Verbindungen zwischen verschiedenen Darstellungsformen (Rechengeschichten, konkrete Handlungen, bildhafte Darstellungen, Symbolebene) herstellen zu können. Dass die Lernende zwischen den Darstellungsformen flexibel hin- und her zu übersetzen können, stellt ein bedeutsames Lernziel dar.	Ich kann in Rechengeschichten Malaufgaben enddecken, diese aufschreiben und lösen. Ich kann mir zu Malaufgaben Geschichten ausdenken. Ich kann zu einer Malaufgaben Abbildungen entwickeln, die genau diese Aufgabe erklären. Dazu verwende ich z.B. den Zahlenstrahl. Wenn sich die Aufgabe 6•2 darstellen will, zeichne ich dann 6 Zweiersprünge ein. Ich kann Malaufgaben in Plusaufgaben umwandeln.	Rechengeschichten erfinden Lernende erfinden Rechengeschichten zur Multiplikation und stellen diese szenisch dar. Andere Lernende werden aufgefordert die Rechengeschichte zu deuten und als Malaufgabe zu formulieren. Weitere Informationen (Selter u.a. 2014)
					Drittens gehört zum umfassendes Verständnis der Multiplikation, dass die Lernenden Beziehungen zwischen den Malaufgaben erkennen, beschreiben und als Rechenstrategie nutzen können. Kernaufgaben Nachbaraufgaben Tauschaufgaben Verdoppeln Bezug auf Multiplikation mit Zehn	Ich kann Malaufgaben schneller lösen, wenn ich sie in Aufgaben überführe, die ich mir schon fest eingeprägt habe. Z. B. habe ich mir die 5er Malfolge schon gut eingeprägt, während ich bei der 7er Malfolge noch unsicher bin. Deshalb tausche ich die Faktoren bei der Aufgabe 5•7. Für die Aufgabe 7•5 weiß ich das Ergebnis dann sofort. Die Aufgabe 6•7 ist für mich auch noch schwer. Deshalb splitte ich diese Aufgabe in zwei Teilaufgaben auf. Ich rechne 5•7, addiere zum Ergebnis 7 und schon habe ich diese Aufgabe gelöst.	Kernaufgaben finden und für Lösung schwererer Aufgaben nutzen Es gibt Malaufgaben die schnell beherrscht werden (in der Regel Malaufgaben, in denen der erste Faktor 1, 2, 5 oder 10) lautet. Diese werden Kernaufgaben genannt und individuell ermittelt, im Hunderterfeld markiert und in Bezug auf Beziehungen zwischen den Malaufgaben diskutiert. Auf der Basis der Abbildung kann gemeinsam mit den Kindern beraten werden, wie durch Aufgabenzerlegung diese Kernaufgaben erzeugt und so Rechenstrategien für die Lösung „schwerer Aufgaben“ gefunden werden können (Tauschaufgaben, Nachbaraufgaben, Verdoppeln, Zehnertrick)
					Die Lernenden können eine Malaufgabe in symbolischer Schreibweise richtig deuten. Sie kennen die Konvention, dass die erste Zahl in einer Malaufgabe angibt, wie viele gleichgroße Gruppen vorliegen und dass die zweite Zahl beschreibt, wie groß diese Gruppen sind. Die Vertauschbarkeit der Zahlen hat für das Ergebnis der Multiplikation keine Bedeutung (3 mal 4 ist ebenso 12 wie 4 mal 3). Zu unterscheiden ist aber der Multiplikand (steht für die Anzahl) und der Multiplikator (wie oft). 3 mal 4 beinhaltet die dreimalige Addition der Anzahlen 4+4+4. Hingegen beinhaltet 4 mal 3 die viermalige Addition der Anzahlen 3+3+3+3. Welche Zahl für welche Rolle steht, muss assoziativ angewendet werden können.	Ich weiß, welche Bedeutung die Symbole in einer Malaufgabe haben und kann sie erklären. Die erste Zahl gibt an, wie viele Gruppen es gibt und die zweite Zahl, wie groß die Gruppen sind. Die Aufgabe 3•4 kann dann z.B. drei Viererreihen in einem Punktefeld bedeuten und die Gesamtzahl der Punkte ist gesucht. Dafür steht das Malzeichen. Ich weiß, dass das Vertauschen der beiden Zahlen für das Ergebnis einer Malaufgabe keine Bedeutung hat. Bei der Aufgabe 3•4 müsste ich 4+4+4=12 rechnen. Bei der Aufgabe 4•3 müsste ich 3+3+3+3=12 rechnen. Auch wenn das Ergebnis gleich ist, müsste ich mir für die Aufgaben unterschiedliche Geschichten ausdenken. Z.B. passt die Aufgabe 3•4 zu der Geschichte, dass Tina 3 mal zur Apfelkiste läuft und jeweils 4 Äpfel mitbringt. Die Aufgabe 4•3 wiederum könnte erzählen, dass Tina 4 mal zur Kiste läuft und jeweils 3 Äpfel mitbringt.	Ausführliche Erläuterungen zum sicheren Rechnen des kleinen Einmaleins, Übungsangebote und Material (MAHIKO Malaufgaben sortieren) Die Beziehungen zwischen den Zahlen können durch die Einmaleins-Tafel (Wittmann/Müller: Mathe 2000) verdeutlicht werden, die sich dadurch von reinen Auslernpostern unterscheidet!
					Aufbauend auf dem umfassenden Verständnis der Multiplikation prägen sich Lernenden die Malfolgen des kleinen Einmaleins (von leicht zu schwer) sukzessive ein, um schnell und flexibel und unter Nutzung von Rechenstrategien Malaufgaben lösen zu können. Beziehungen zwischen den Zahlen werden durch die Einmaleins-Tafel veranschaulicht.	Ich kann die Malfolgen meist aus dem Gedächtnis aufsagen. Wenn mir Lösungen nicht gleich einfallen, kenne ich Tricks, wie ich mir das Ergebnis über Nachbaraufgaben oder Tauschaufgaben herleiten kann.	Weitere Anregungen: DZLM Operationsverständnis allgemein (DZLM: Digitale Pinnwand zum Operationsverständnis Multiplikation
					Grundvorstellungen Division: Ein umfassendes Verständnis der Division basiert auf zwei Grundvorstellungen, die das Geteiltzeichen mit Inhalt füllen: -Vorstellung von Situationen des Aufteilens: Gesucht ist die Anzahl der Teilmengen, während die Gesamtmenge und die Gruppengröße gegeben sind. Z.B.: 12 Äpfel (Gesamtmenge) sind gegeben, die sollen eingetütet werden, wobei immer 3 Äpfel (Gruppengröße) in einer Tüte verpackt werden sollen. Die Anzahl der Tüten (Anzahl der Teilmengen) ist gesucht. -Die Vorstellung von Situationen des Verteilens: Gesucht ist die Gruppengröße, während die Gesamtmenge und die Anzahl der Teilmengen gegeben sind. Z.B.: Tom hat 12 Äpfel (Gesamtmenge), die sollen an drei Freunde (Anzahl der Teilmengen) verteilt werden. Wieviel Äpfel (Gruppengröße) bekommt jeder Freund? Die Vorstellungen des Aufteilens und des Verteilens sind eng mit den Vorstellungen zur Multiplikation verknüpft. Die Lernenden verstehen, dass die Division die Umkehroperation zur Multiplikation ist. Diese Grundvorstellungen ermöglichen den Lernenden ein umfassendes Verständnis zur Operation der Division, das es ihnen ermöglicht - flexibel und sicher Divisionsaufgaben in verschiedenen Kontexten zu deuten, - die Aufgaben der Divisionsreihen zueinander in Beziehung zu setzen - und den engen Zusammenhang zur Multiplikation zu verstehen und zu nutzen. (ausführliche Erläuterung in: MAHIKO Division verstehen – Grundlagen).	Ich kann in Erzählungen oder Handlungen, in denen etwas gerecht aufgeteilt werden soll, eine Geteiltaufgabe entdecken. Wenn ich z.B. 12 Äpfel habe und diese so in Tüten packen soll, dass jede Tüte 3 Äpfel enthält, kann ich durch eine Geteiltaufgabe (12:3=?) ausrechnen, dass ich 4 Tüten brauche. Ich weiß, dass das Ergebnis stimmt, denn 4 mal 3 Äpfel ergibt die Aufgabe 4•3=12. Ich kann in Erzählungen oder Handlungen, in denen etwas gleichmäßig verteilt werden soll, eine Geteiltaufgabe entdecken. Wenn ich z.B. meine 12 Äpfel gerecht unter meinen drei Freunden verteilen will, kann ich durch die Geteiltaufgabe 12:3=? ausrechnen, wieviel Äpfel jeder Freund bekommen wird. Jeder Freund bekommt 4 Äpfel. Meine 3 Freunde haben also zusammen 12 Äpfel, denn 4•3=12. Geteilaufgabe. Ich weiß, dass jede Geteiltaufgabe in eine Malaufgaben überführt werden kann. Wenn ich z.B. 8:4 teile, ist das Ergebnis 2. Wenn ich das Ergebnis mit 4 malnehme, komme ich wieder zu der ersten Zahl der Geteiltaufgabe. Die Aufgaben 8:4=2 und 2•4=8 gehören eng zusammen. Es sind Umkehraufgaben.	Prozessbezogene Kompetenzen: Bei allen Übungen zur Division sind die sprachliche Begleitung der Aufgabenlösung, die Begründung der Entscheidungen, die Bezugsetzung zur Multiplikation sowie Diskussionen innerhalb Lerngruppe wichtig. Die Fachbegriffe werden ausgehend von konkreten Situationen eingeführt und für die symbolische Nutzung vertieft. Um zu vermeiden, dass zur Division lediglich ein auswendig gelerntes Einsdurcheins angewendet wird, sind die Lernenden dabei zu unterstützen, Divisionsaufgaben in Alltags- und Lernsituationen zu erkennen und flexibel und sicher zu lösen. Sie werden angeleitet, Division (Prozess des Aufteilens oder Verteilens) als Umkehr des Vervielfachens aus der Multiplikation zu verstehen. Zur Unterstützung der angezielten Verstehensprozesse eignen sich die folgenden 4 Aufgabentypen, Ausführliche Beispiele (MAHIKO: Division verstehen/Übungen)
					Aus Alltagssituationen ist den Lernenden bekannt, dass Handlungen des Verteilens und des Aufteilens oft nicht „gerecht“ gelingen können. Aufbauend auf diesem Alltagsverständnis verstehen sie den Vorgang der Division mit Rest (R=?), die dann entsteht, wenn der Dividend nicht ein Vielfaches des Divisors ist. Die Lernenden erkennen durch diese Übungen, dass Geteiltaufgaben auch linear durch „Sprünge“ an Malreihen dargestellt werden können. Malreihen entstehen durch die lineare Anordnung von Punkten auf dem Zahlenstrahl, wobei entsprechend der jeweiligen Malreihe die notwendigen Sprünge (z.B. Dreiersprünge bei der Dreierreihe) farblich abgesetzt werden.	Ich weiß, dass das Verteilen oder Aufteilen nicht immer gerecht möglich ist. So bleiben z.B. 2 Äpfel übrig, wenn ich 14 Äpfel unter meinen drei Freunden verteilen will. Ich weiß, dass diese Aufgabe eine Geteiltaufgabe mit Rest darstellt (14:3=4 R2 ). Ich überlege mir, was ich mit den übrigen Äpfeln machen könnte, damit doch noch alle Äpfel gerecht verteilt werden könnten. Ich kann in Rechengeschichten Geteiltaufgaben entdecken, diese aufschreiben und lösen. Ich kann mir zu Geteiltaufgaben Geschichten ausdenken. Ich kann zu einer Geteiltaufgabe Abbildungen entwickeln, die genau diese Aufgabe darstellen. Dazu verwende ich z.B. Plättchen oder den Zahlenstrahl. Wenn sich die Aufgabe 12:3 darstellen will, ordne ich die 12 Plättchen in vier Reihen mit je drei Plättchen an. Auf dem Zahlenstrahl suche ich die 12 und zeichne dann rückwärts die Dreiersprünge bis zum Anfang des Zahlenstrahls ab. Ich kann Geteiltaufgaben in Minusaufgaben umwandeln und erklären, warum das geht und wie das geht. Aus der Aufgabe 12 : 3=4 z.B., entsteht die passende Minusaufgabe, wenn ich von der 12 viermal die 3 abziehe: 12-3-3-3-3=0.	(1) Geteiltaufgaben in der Umwelt. Alltagssituationen des Verteilens und Aufteilens erzählen und mit Material veranschaulichen. Die Lernenden auffordern, das Dargestellte als Situation des Aufteilens/Verteilens zu beschreiben und diese Zuschreibungen zu begründen. Im Anschluss wird die Alltagssituation mit der passenden Geteiltaufgabe verknüpft, notiert und ausgerechnet. (2) Geteiltaufgaben am Hunderterfeld erkennen und im Hunderterfeld entwickeln. Geteiltaufgaben werden flächig auf dem Hunderterpunktefeld mithilfe eines Malwinkels dargestellt. Anhand des Musters sollen die Lernenden die veranschaulichte Geteiltaufgabe sowie die dazu gehörige Malaufgabe finden, benennen und diese Zuordnungen begründen. Anschließend entwickeln die Lernenden selbständig Muster auf dem Hunderterfeld, die als Geteiltaufgabe/Malaufgabe diskutiert, notiert und gelöst werden (kommuniziert, dargestellt). (3) Geteiltaufgaben auf der Malreihe entdecken und diskutieren Vorgegeben Geteiltaufgaben werden in den Malreihen entdeckt, benannt, begründet und mit der dazugehörigen Malaufgabe und zur wiederholten Subtraktion in Beziehung gesetzt (4 ) Übungen zur Verknüpfung verschiedener Darstellungsformen: Was passt? Die Lernenden werden aufgefordert Rechengeschichten, Rechenaufgaben und Bilder von didaktischem Material bzw. Alltagsbilder zur Division einander zu zuordnen. Dabei wird die Verknüpfung der verschiedenen Darstellungsformen geübt und gefestigt. Die Lernenden müssen nicht zwischen diesen Grundvorstellungen des Verteilens und Aufteilens unterscheiden, sollten diese aber in entsprechenden Situationen als Geteiltaufgaben erkennen können. Geteiltaufgaben mit Rest sollten in alle Aufgabentypen und allen Darstellungsformen einbezogen, diskutiert und gelöst werden. Wenn die Aufgabe auf eine Alltagssituation bezogen wird, sollten die Lernenden nach praktischen Möglichkeiten des „gerechten“ Verteilens und Aufteilens suchen. Dadurch wird Verständnis für das Rechnen mit Dezimalzahlen und Brüchen vorbereitet.
					Prozessbezogene Kompetenzen Die Lernenden stellen Verbindungen zwischen den verschiedenen Darstellungsformen (Rechengeschichten, konkrete Handlungen, bildhafte Darstellungen, Symbolebene) her und tauschen sich darüber aus (argumentieren, kommunizieren). Sie lernen zu beschreiben, wie eine sukzessive Subtraktion als Divisionsaufgabe dargestellt und gelöst werden kann.		Rechengeschichten erfinden Lernende erfinden Rechengeschichten zur Division (mit und ohne Rest) und stellen diese bildnerisch oder szenisch dar. Andere Lernende werden aufgefordert die Rechengeschichte zu deuten und als Geteiltaufgabe zu formulieren.
					Die Lernenden erkennen Beziehungen zwischen den Geteiltaufgabenreihen und zu den Umkehraufgaben der Multiplikation, können diese beschreiben und als Rechenstrategie nutzen können. Das Lösen und Einprägen der Geteiltaufgaben basiert auf bereits vorhandenen Kompetenzen im Bereich der Multiplikation. Die Lernenden erkennen (selbstständig oder angeleitet, demonstriert) das Prinzip der Umkehraufgabe, dass auf der Frage zur Geteiltaufgabe beruht, wie häufig man die zweite Zahl dieser Aufgabe malnehmen muss, um die erste Zahl zu erreichen.	Ich kann Geteiltaufgaben schneller lösen, wenn ich sie in Aufgaben überführe, die ich mir schon fest eingeprägt habe und ich kann erklären, wie das geht. Da ich weiß, dass Malaufgaben die Umkehraufgaben zu den Geteiltaufgaben sind, kann ich mir das Ergebnis der Geteiltaufgabe aus den Malaufgaben ableiten, die ich mir schon fest eingeprägt habe. Ich kann für mich komplizierte Geteiltaufgaben in Teilaufgaben aufsplitten und so schnell zum Ergebnis kommen. Die für mich leichten Teilaufgaben rechne ich aus. Je nachdem, ob die erste Zahl meiner ersten Teilaufgabe größer oder kleiner als die Gesamtzahl in der schwierigen Aufgabe ist, muss ich die Ergebnisse der Teilaufgaben addieren oder subtrahieren.	Sicheres Rechnen im kleinen Einsdurcheins (Ausführliche Beschreibung von Grundlagen und Übungen zum sicheren Rechnen im Bereich des kleinen Einsdurcheins: (MAHIKO Sicher im 1durch1 – Grundlagen): - Nutzung bereits erworbener Kompetenzen im Bereich der Multiplikation Lernende erhalten Anregungen dazu, die Aufgaben des kleinen Eindurcheins aus den entsprechenden und bereits bekannten Aufgaben des kleinen Einmaleins abzuleiten. - Erkundung und Nutzung von Rechenstrategien zur Lösung schwieriger Aufgaben Die Lehrkräfte ermitteln individuell ausgeprägte Kernaufgaben (s.o., in der Regel Geteiltaufgaben mit den Ergebnissen 1, 2, 5, 10) und demonstrieren den Lernenden, wie schwierige Aufgaben durch das Bilden von Teilaufgaben gelöst werden können. Diese Verfahrensweise sollte handlungsbegleitend kommentiert, in der Lerngruppe besprochen und geübt werden.
					Die Lernenden können eine Divisionsaufgabe in symbolischer Schreibweise richtig deuten. Sie kennen die Konvention, dass die erste Zahl (Dividend) in einer Divisionsaufgabe die Gesamtzahl angibt, die geteilt werden soll. Die zweite Zahl (Divisor) ist die, durch die geteilt werden soll. Sie gibt die Größe jeder Gruppe an. Das Ergebnis (Quotient) informiert über die Anzahl der Gruppen, die durch die Teilung entstehen.	Ich weiß, welche Bedeutung die Zahlen und das Rechenzeichen in einer Geteiltaufgabe haben und kann das erklären. Die erste Zahl gibt die Gesamtzahl an. Z.B. könnten 12 Äpfel zur Verfügung stehen, die aufgeteilt werden sollen. Für der Aufteilung oder Verteilung steht das Geteiltdurchzeichen (:). Die zweite Zahl ist die Zahl durch die geteilt werden soll. Bei der Aufgabe 12:4 ist das die 4 und das bedeutet, dass durch die Teilung Vierer-Gruppen entstehen sollen. Das Ergebnis sagt an, wie viele Vierergruppen aus 12 gebildet werden können.	Erklärvideos für Lernende zur Division MAHIKO: -Geteiltaufgaben an der Punktereihe: -MAHIKO: Schwierige Geteiltaufgaben lösen:
					Aufbauend auf dem umfassenden Verständnis der Division prägen sich Lernenden die Aufgaben des kleinen Einsdurcheins (ausgehend von den Kernaufgaben und abgeleitet von den Kernaufgaben) sukzessive ein. Von der Multiplikation kennen sie Zahlentripel (1. Faktor, 2. Faktor, Produkt) und nutzen die Kenntnisse dieser Zahlentripel zum Lösen von Divisionsaufgaben. Dabei nutzen sie bereits vorhandene Kompetenzen im Bereich der Multiplikation (Umkehraufgaben), um schnell und flexibel und unter Nutzung von weiteren Rechenstrategien Divisionsaufgaben lösen zu können.	Ich kann die Geteiltaufgaben im Zahlenraum bis 100 schnell und flexibel lösen. Wenn mir Lösungen nicht gleich einfallen, kenne ich Tricks, wie ich mir das Ergebnis über entsprechende Malaufgaben, Nachbaraufgaben, zerlegen der Aufgabe in Teilaufgaben herleiten kann. Diese Tricks (Rechenstrategien) kann ich erklären und begründen.
					Die Lernenden übertragen die Grundaufgaben des Kopfrechnens auf analoge Aufgaben im Zahlenraum bis zur Million. Die Lernenden nutzen die Zerlegung der 10 für das Ergänzen zum nächsten Zehner, das Ergänzen zum nächsten Hunderter, das Ergänzen bis 1000 und zum Ergänzen bis 1 Million. - Die Lernenden nutzen die Strukturen des Verdoppelns/Halbierens im Zwanzigerraum im Hunderterraum, im Tausenderraum, im Millionenraum. - Die Lernenden nutzen Strategien, die sie im kleinen Zahlenraum nutzen, auch in größeren Zahlenräumen: Tauschaufgaben (3+8=8+3), Nutzen von Nachbaraufgaben (10+8 / 9+8), schrittweises Rechnen (6+8=6+4+4), … - Die Lernenden legen mit Mehrsystemblöcken oder mit Plättchen in der Stellentafel Zahlen, die die gleiche Anzahl Bündel haben, jedoch von unterschiedlichen Einheiten, z.B. 7, 70, 700, 7000, … oder 23, 230, 2300, … und erklären wie sich die Zahl verändert, wenn eine größere Bündelungseinheit verwendet oder die 7 Plättchen von der Einer- zur Zehnerstelle geschoben werden.	Ich kann Aufgaben mit kleineren Zahlen nutzen, um Aufgaben mit großen Zahlen (bis zur Million) im Kopf zu rechnen. Ich kann die Zehnerzerlegung („verliebten Zahlen“, „Zehnerfreunde“) nutzen, um Zahlen bis zum nächsten Zehner, Hunderter, Tausender und bis zur Millionen zu nutzen. Ich kann Verdopplungs- und Halbierungsaufgaben nutzen, um mit großen Zahlen zu rechnen, z.B. weiß ich, dass 7+7=14 und 700+700=14000. Ich kann Strategien, die ich beim Rechnen mit kleinen Zahlen anwenden kann, auch mit großen Zahlen anwenden, z.B. Tauschaufgaben (3+8=8+3) Nachbaraufgaben (10+8 / 9+8) oder schrittweises Rechnen (6+8=6+4+4). Ich kann mit Mehrsystemblöcken oder Stellenwerttafel erklären, warum man die Aufgaben und Strategien aus dem kleinen Zahlenraum auch im großen Zahlenraum nutzen kann.	Analogien können mit Hilfe der Stellentafel, Stellenwertkarten und Mehrsystemblöcken verdeutlicht werden. Wichtig ist die Verknüpfung der verschiedenen Darstellungen. Dafür können z.B. folgende Rechnungen mit den Mehrsystemblöcken gelegt werden, die Zahlen in Stellenwerttafeln notiert werden und die Rechnungen dazu geschrieben werden: 6+7 60+70 600+700 6000+7000 8+5 18+15 118+115 oder 108+105 Fragen dazu stellen: Wie verändert sich der Einer/Zehner/Hunderter? Wo wird gebündelt? Wie könnte es weitergehen? Wichtige Erläuterungen zum Kopfrechnen: https://primakom.dzlm.de/inhalte/zahlen-und-operationen/kopfrechnen/unterricht
					Die Lernenden verstehen mündliche und halbschriftliche Rechenstrategien zu den vier Grundrechenarten und setzen diese flexibel ein. Teilziele: - Die Lernenden können die halbschriftlichen Verfahren mit Hilfe von Material (Addition und Subtraktion: Mehrsystemblöcke, Rechenstrich; Multiplikation: Kästchenpapier) durchführen, protokollieren und erklären (prozessbezogene Kompetenz: Darstellen). - Die Lernenden können erklären, warum und wie die Strategien funktionieren. - Die Lernenden vollziehen die Strategien anderer Lernenden nach. - Die Lernenden begründen, welche Strategie sie bei einer Aufgabe anwenden würden (ohne die Aufgabe zu rechnen). - Die Lernenden können Aufgaben und Strategien miteinander vergleichen, so dass sie geeignete Strategien für das Lösen der Aufgaben auswählen können. Die Lernenden verstehen: Es gibt nicht eine beste Strategie, sondern die Strategie soll in Abhängigkeit von gegebenen Zahlenwerten und den eigenen Präferenzen gewählt werden. - Die Lernenden zerlegen Aufgaben in einfachere Teilaufgaben und notieren die einzelnen Rechenschritte, bis das Ergebnis ermittelt ist.	Ich kann Additions-, Subtraktions-, Multiplikations- und Divisionsaufgaben mit halbschriftlichen Strategien lösen und meine Vorgehensweise erklären. Teilziele: Ich kann mit Material oder mit Zeichnungen, z.B. am Rechenstrich, Rechnungen halbschriftlich lösen, indem ich die einzelnen Schritte lege oder zeichne und die passende Rechnung notiere. Ich kann erklären, warum und wie die Strategien funktionieren. Ich kann erkennen, welche halbschriftlichen Strategien andere Kinder angewendet haben und die gleiche Strategie anwenden. Ich kann begründen, welche Strategie zum Lösen einer Aufgabe besonders gut geeignet ist. Ich kann verschiedene Strategien miteinander vergleichen. Wenn ich Aufgaben halbschriftlich löse, dann kann ich die Aufgabe in einfachere Teilaufgaben zerlegen und die einzelnen Rechenschritte notieren.	Erläuterungen und Überblick über die halbschriftlichen Strategien: https://primakom.dzlm.de/inhalte/zahlen-und-operationen/halbschriftliche-rechenstrategien/unterricht https://pikas.dzlm.de/schumas/arithmetik-12/modul-4/mini-module/42-halbschriftliche-strategien Lernvoraussetzungen: - Die Lernenden können sich im entsprechenden Zahlenraum sicher orientieren. - Sie können die notwendigen Anschauungsmittel zu Zahl- und Operationsdarstellungen (Rechenstrich, Mehrsystemblöcke, …) sachgerecht nutzen.
					Addition Schrittweise: Die Lernenden zerlegen den zweiten Summanden, so dass einfachere Zwischenaufgaben entstehen. Stellenweise: Die Lernenden zerlegen beide Summanden stellengerecht. Hilfsaufgabe: Die Lernenden nutzen eine ähnliche Aufgabe, die einfacher zu rechnen ist, z.B. 38+39=(38+40)–1 Vereinfachen: Die Lernenden nutzen eine ähnliche Aufgabe, bei der beide Summanden verändert werden und somit der Korrekturschritt entfällt, z.B. 38+39=37+40	Addition Ich kann eine Additionsaufgabe mit der Strategie „Schrittweise“ lösen. Dabei zerlege ich den zweiten Summanden in Hunderter, Zehner und Einer und addiere sie zum ersten Summanden. Ich kann eine Additionsaufgabe mit der Strategie „Stellenweise“ lösen. Dabei zerlege ich beide Summanden in Einer, Zehner und Hunderter und addiere sie stellenweise. Ich kann Additionsaufgaben mit einer ähnlichen Aufgabe, also einer Hilfsaufgabe lösen, z.B. 38+39=(38+40)–1. Ich kann Additionsaufgaben so verändern, dass ich sie einfacher lösen kann. Dabei verändere ich beide Summanden, z.B. z.B. 38+39=37+40.	Aktivitäten im Unterricht Die Lernenden versuchen die Strategien anderer (evtl. fiktiver) Lernenden nachzuvollziehen. Die Lernenden überlegen, welche Strategie für eine Aufgabe am besten geeignet ist und ordnen Aufgaben den Strategien zu. (Das Ausrechnen kommt später.)
					Subtraktion: Schrittweise: Die Lernenden subtrahieren vom Minuenden stellenweise den Subtrahenden, z.B. zuerst die Hunderter, dann die Zehner und dann die Einer. Sie zerlegen dafür den Subtrahenden. Stellenweise: Die Lernenden zerlegen den Minuend und Subtrahend in ihre Stellenwerte und subtrahieren sie jeweils und addieren am Ende die einzelnen Ergebnisse. Vereinfachen: Die Lernenden verändern Minuend und Subtrahend gleichsinnig, um die Differenz zu berechnen, z.B. 345-198 = 347-200 Ergänzen: Die Lernenden ergänzen schrittweise vom Subtrahenden zum Minuenden, wobei das, was bei den Teilschritten ergänzt wird, die Differenz ergibt. (Lässt sich gut am Rechenstrich verdeutlichen.)	Subtraktion Ich kann Subtraktionsaufgaben mit der Strategie „Schrittweise“ lösen. Dabei zerlege ich den Subtrahenden in seine Stelenwerte und ziehe sie schrittweise ab. Ich kann Subtraktionsaufgaben mit der Strategie „Stellenweise“ lösen. Dabei zerlege ich beide Zahlen in ihre Stellenwerte und ziehe sie voneinander ab. Ich kann Subtraktionsaufgaben so verändern, dass ich sie einfacher lösen kann, z.B. 345-198 = 347-200. Ich kann Subtraktionsaufgaben lösen, indem ich vom Subtrahenden zum Minuenden ergänzen (und meine Rechnung am Rechenstrich einzeichne).	halbschriftliche Rechenstrategien sind neben dem Kopfrechnen, dem schriftlichen Rechnen und dem Taschenrechner ein sinnvoller und oftmals sehr ökonomischer Weg, um Aufgabenstellungen zu lösen. bereiten Kopfrechenstrategien in größeren Zahlenräumen vor sind die Grundlage, um die schriftlichen Strategien zu verstehen. Dieses Verständnis ist wesentlich, um die schriftlichen Algorithmen richtig ausführen zu können
					Multiplikation: Stellenweise: Die Lernenden zerlegen beide Faktoren in ihre Stellenwerte und addieren die Teilergebnisse. Schrittweise: Die Lernenden zerlegen nur einen Faktor in seine Stellenwerte, multiplizieren sie mit dem anderen Faktor und addieren die Teilergebnisse. Vereinfachen: Die Lernenden verändern beide Faktoren nach dem Gesetz der Konstanz des Produkts gegensinnig, z.B. 12x15 = 6x30 Hilfsaufgabe: Die Lernenden nutzen eine Aufgabe, die leichter zu rechnen ist und addieren oder subtrahieren anschließend die Differenz, z.B. 12x29 = (12x30)-12	Multiplikation Ich kann Multiplikationsaufgaben stellweise lösen, indem ich beide Faktoren in ihre Stellenwerte zerlege und die Teilergebnisse addiere, z.B. mit Hilfe des Malkreuzes. Ich kann Multiplikationsaufgaben vereinfachen, um sie zu lössen, indem ich die Faktoren gegensinnig verändere, z.B. 12x15 = 6x30. Ich kann Multiplikationsaufgaben lösen, indem ich Hilfsaufgaben nutze, , z.B. 12x29 = (12x30)-12.	Erläuterungen zur halbschriftliche Multiplikation: https://kira.dzlm.de/arithmetik/halbschriftliches-rechnen/halbschriftliche-multiplikation
					Division: Schrittweise: Die Lernenden zerlegen den Dividenden in Zahlen, die sie gut teilen können. Hilfsaufgabe: Die Lernenden lösen eine Divisionsaufgabe, indem sie eine leichter zu lösende Hilfsaufgabe lösen, wobei es sich meist um benachbarte oder Analogieaufgaben handelt. Vereinfachen: Die Lernenden multiplizieren Dividend und Divisor mit der gleichen Zahl, um eine leichtere Rechnung mit gleichem Ergebnis zu lösen. Umkehraufgabe: Die Lernenden bilden aus der Divisionsaufgabe eine passende Multiplikationsaufgabe, um sie zu lösen.	Division Ich kann Divisionsaufgaben schrittweise lösen, indem ich den Dividenden in Zahlen zerlege, die ich gut teilen kann. Ich kann Divisionsaufgaben lösen, indem ich eine Hilfsaufgabe nutze, z.B. 232:8=(240:8)-(8:8). Ich kann eine Divisionsaufgabe lösen, indem ich sie vereinfache, z.B. anstatt geteilt durch 4, rechne ich geteilt durch 2 und dann nochmal geteilt durch 2. Ich kann Divisionsaufgaben lösen, indem ich die passende Multiplikationsaufgabe als Umkehraufgabe nutze, z.B. 360:4 à 90×4=360	Erläuterungen zur Division: https://kira.dzlm.de/arithmetik/halbschriftliches-rechnen/halbschriftliche-division schrittweise: 482:2=241 400:2=200 80:2= 40 2:2= 1 124:4= 31 124:2= 62 62:2= 31 Hilfsaufgabe: 232:8=29 240:8=30 8:8= 1 Vereinfachen: 225:25= 9 450:50= 9 Umkehraufgabe: 360:4= 90 90 × 4=360
					Die Lernenden verstehen schriftliche Verfahren der Addition, Subtraktion und Multiplikation, beschreiben den Algorithmus, führen diesen geläufig aus und wenden ihn bei geeigneten Aufgaben an. Teilziele: Addition: Die Lernenden bündeln immer 10 einer Bündelungseinheit zur nächstgrößeren Bündelungseinheit. Die Lernenden vergleichen die halbschriftliche Strategie „Stellenweise“ mit dem Algorithmus. Subtraktion: Die Lernenden entbündeln eine Einheit, wenn eine Ziffer des Subtrahenden größer ist als die Ziffer des gleichen Stellenwert beim Minuenden. Die Lernenden können eines der Verfahren zu schriftlichen Subtraktion beschreiben und anwenden (Auffüllen, Erweitern, Entbündeln). Multiplikation: Die Lernenden können das Lösen von Multiplikationsaufgaben am Malkreuz und den schriftlichen Algorithmus vergleichen.	Ich kann Additions-, Subtraktions- und Multiplikationsaufgaben schriftlich lösen und meine Vorgehensweise beschreiben. Addition Ich weiß, dass ich bei der schriftlichen Addition immer 10 zur nächstgrößeren Einheit bündeln muss ich weiß, was der Übertrag bedeutet. Ich kann die schriftliche Addition mit der Strategie „Stellenweise“ bei der halbschriftlichen Addition vergleichen. Subtraktion Ich kann erklären, dass die 1 im Übertrag bedeutet, dass ich eine Einheit vom nächstgrößeren Stellenwert entbündeln muss. Ich kann Subtraktionsaufgaben mit dem gelernten Verfahren schriftlich lösen. Multiplikation Ich kann die schriftliche Vorgehensweise beim Lösen von Multiplikationsaufgaben mit dem Vorgehen am Malkreuz vergleichen.	Lernvoraussetzungen: - Orientierung im Zahlenraum: Zahlen sind z.B. aus Einern, Zehnern und Hundertern zusammengesetzt, Zahlen in der Stellentafel darstellen - Halbschriftliche Strategie „stellenweise" - Verständnis des Bündelungsprinzips und der Stellenschreibweise, z.B. 12 Zehner = 120 - Rolle der Null
					Die Lernenden kontrollieren Lösungen durch geeignete Vorgehensweisen, z. B. Überschlagsrechnung, Umkehroperation. Teilziele: Die Lernenden runden Zahlen „regelkonform“ auf den nächsten Zehner oder Hunderter, um mit diesen Zahlen eine Überschlagsrechnung durchzuführen. Die Lernenden reflektieren, inwieweit das Ergebnis der Überschlagsrechnung die Fragestellung beantwortet bzw. inwieweit sie zum genau gerechneten Ergebnis passt. Die Lernenden prüfen Ergebnisse mit Hilfe der Umkehraufgaben.	Ich kann die Lösung von Rechnungen kontrollieren, indem ich eine Überschlagsrechnung mache oder bei der Subtraktion und Division die Umkehrrechnung mache. Ich kann Zahlen runden: Bei Ziffern kleiner als 5 runde ich ab und bei den Ziffern 5 und größer runde ich auf. Ich kann die Lösung meiner Rechnung mit der Überschlagsrechnung vergleichen und einschätze, ob meine Lösung stimmen kann. Ich kann die Umkehraufgabe nutzen, um meine Rechnung zu überprüfen. Dies mache ich vor allem bei der Subtraktion und Division.	Überschlagsrechnen: https://kira.dzlm.de/arithmetik/%C3%BCberschlagsrechnen Unterrichtsaktivitäten: Fragestellungen: Reicht das Geld? Wie viel Geld sollte Kind x mitnehmen? Umkehroperationen sind für die Lernenden vor allem bei der Subtraktion und Division hilfreich.
					Natürlich Zahlen darstellen Lernende stellen ganze Zahlen auf verschiedene Weise dar (z.B. Zahlenstrahl/-gerade, Zifferndarstellung, Stellenwerttafel, Wortform), nutzen sinntragende Vorstellungen von natürlichen Zahlen entsprechend der Verwendungsnotwendigkeit, runden Zahlen.	Stellenwertverständnis Ich kann Zahlen, die mit Material gelegt sind, und Zahlbilder lesen. Ich kann Zahlen mit Material und Zahlbildern darstellen. Ich kann bündeln und entbündeln. Ich kann Zahlen in der Stellenwerttafel ablesen und darstellen. Ich kann Zahlen in der Stellenwerttafel ordnen. Ich kann Additionen in der Stellentafel ablesen und darstellen. Ich kann in der Stellentafel Aufgaben wie „mal 10“ oder „durch 100“ darstellen. Ich kann Zahlen runden. Zahlenstrahl Ich kann Zahlen am Zahlenstrahl lesen und darstellen. Ich kann Zahlen miteinander vergleichen und der Größe nach ordnen. Ich kann zu Zahlen Nachbarzahlen angeben und in Schritten zählen. Ich kann Zahlen auf dem Zahlenstrahl eintragen. Ich kann Zahlen am Zahlenstrahl ungefähr anordnen. Ich kann am Zahlenstrahl Additions- und Subtraktionsaufgaben darstellen.	Stellenwertverständnis: https://mathe-sicher-koennen.dzlm.de/material-sek/natuerliche-zahlen Handlungsorientierte Aktivitäten für die ganze Klasse: https://mathe-sicher-koennen.dzlm.de/mskfiles/uploads/Dokumente/msk-5minkartei_210225.pdf Erklärvideo für die Lernenden zu Zahlen mit Material lesen und darstellen: https://www.youtube.com/watch?app=desktop&v=LLrpUYXM2-Y&feature=youtu.be zu Zahlen am Zahlenstrahl lesen und darstellen: https://www.youtube.com/watch?v=QWqzEEGy62A
					mit natürlichen Zahlen rechnen Lernende führen Grundrechenarten (Kopfrechnen und schriftliche Rechenverfahren) mit natürlichen Zahlen (Addition/Subtraktion aus), nutzen Überschlagsrechnungen zur Orientierung und zur Kontrolle, nutzen sinntragende Vorstellungen von Operationen rationaler Zahlen (z. B. schrittweiser, halbschriftlicher Verfahren), rechnen mit natürlichen Zahlen, die im täglichen Leben vorkommen, sowohl zur Kontrolle als auch im Kopf und erklären die Bedeutung der Rechenoperationen.	Ich kann zwei und mehr Zahlen schriftlich addieren. Ich kann zwei und mehr Zahlen schriftlich subtrahieren. Ich kann auf mehreren Wegen addieren und subtrahieren. Ich kann Multiplikationen in Bildern erkennen und darstellen. Ich kann mit dem Malkreuz multiplizieren. Ich kann Zahlen schriftlich multiplizieren. Ich kann beim Multiplizieren das Ergebnis im Kopf überschlagen. Ich kann Multiplikationsaufgaben so umformen, dass man einfacher rechnen kann. Ich kann mit Rest dividieren. Ich kann Zehner-Zahlen dividieren. Ich kann Divisionsaufgaben überschlagen. Ich kann große Zahlen durch Zahlen unter 10 schriftlich dividieren. Ich kann große Zahlen durch Zahlen unter 100 dividieren. Ich kann Divisionen durch Überschlagen kontrollieren. Ich kann zu Situationen passende Rechenaufgaben finden. Ich kann für alle Rechenarten (Addition, Subtraktion, Multiplikation und Division) passende Situationen oder Bilder angeben.	Um das Verständnis der Lernenden zu fördern, ist die sprachliche Begleitung wichtig. Auch damit sie ihr Vorgehen nachvollziehbar beschreiben können. Falls Rechenwege und Vorgehensweisen mit Material dargestellt werden, ist es wichtig, zu den Handlungen die entsprechenden Rechnungen/symbolischen Schreibweisen zu protokollieren.
					Zehnerpotenzen Lernende lesen und schreiben Zahlen in Zehnerpotenz-Schreibweise und erläutern die Potenzschreibweise mit ganzzahligen Exponenten, stellen Zahlen der Situation angemessen dar, z. B. unter anderem in Zehnerpotenzschreibweise.	Ich kann große Zahlen mit Zehnerpotenzen aufschreiben und Zahlen in Zehnerpotenzschreibweise erklären. Ich kann bei Längen, Gewichten, Flächeninhalten und Volumen mit Zehnerpotenzschreibweise zwischen Einheiten umwandeln. Ich kann sehr kleine Zahlen, Anteile und Größen mit negativen Zehnerpotenzen schreiben. Ich kann mit Zahlen in Zehnerpotenzschreibweise rechnerisch umgehen und mir dabei etwas vorstellen.	Dinge aus dem Alltag mit passenden Maßeinheiten beschreiben und in einer Stellentafel notieren, mit der die Maßeinheiten umgerechnet werden können. Dabei können die Lernenden sehen, dass die Einheit rechts jeweils durch Division durch 10 entsteht und diejenige links durch Multiplikation mit 10.
					Rechengesetze Die Lernenden führen Grundrechenarten zusammen, multiplizieren sie aus und faktorisieren sie mit einem einfachen Faktor, nutzen Rechengesetze (z. B. Kommutativ-, Assoziativ-, Distributivgesetz) auch zum vorteilhaften Rechnen. Teilziele Die Lernenden erkennen gemeinsame Teiler in Termen und können einfache Terme durch Ausklammern faktorisieren, faktorisieren Produkte mit Hilfe von binomischen Formeln, nutzen das Kommutativgesetz, um die Reihenfolge von Zahlen oder Variablen bei Addition und Multiplikation zu verändern, wenden das Assoziativgesetz an, um Summen oder Produkte geschickt zu gruppieren, wenden das Distributivgesetz an, um Terme zu multiplizieren und Terme durch Ausklammern zu faktorisieren, erkennen Rechengesetze in Termen und setzen sie gezielt ein, um Terme zu vereinfachen, zu umformen oder zu faktorisieren.	Ich erkenne gemeinsame Teiler in Termen und kann einfache Terme durch Ausklammern faktorisieren. Ich faktorisiere Produkte mit Hilfe von binomischen Formeln. Ich nutze das Kommutativgesetz, um die Reihenfolge von Zahlen oder Variablen bei Addition und Multiplikation zu verändern. Ich wende das Assoziativgesetz an, um Summen oder Produkte geschickt zu gruppieren. Ich wende das Distributivgesetz an, um Terme zu multiplizieren und Terme durch Ausklammern zu faktorisieren. Ich erkenne Rechengesetze in Termen und setze sie gezielt ein, um Terme zu vereinfachen, zu umformen oder zu faktorisieren.	Erklärungen der Konstanzgesetze: https://adi.dzlm.de/rechengesetze
					Binomische Formeln Die Lernende nutzen binomische Formeln als Rechenstrategie.	Ich kann die erste binomische Formel als Bild veranschaulichen. Ich kenne die binomischen Formeln und kann mit ihnen Quadrate und Produkte in Summen und Differenzen umformen. Ich kann zu Zahlen und Termen die Quadrate finden und umgekehrt. Ich erkenne in Summen (und in Differenzen), ob sie sich in ein Quadrat oder ein Produkt umformen lassen und kann die Umformung durchführen. Ich kann längere Terme in mehreren Variablen umformen und vereinfachen.	Die flächige Darstellung sollten die Lernenden bereits von der Multiplikation kennen. Es eignet sich der Einstieg über die Multiplikation von zweistelligen Zahlen, die an Punktefeldern und Malkreuzen dargestellt wird: https://pikas-mi.dzlm.de/leitideen/kontinuit%C3%A4t-herstellen/unterricht-langfristig-denken/hintergrund
					Teiler und Vielfache Die Lernende bestimmen Teiler und Vielfache natürlicher Zahlen und wenden Teilbarkeitsregeln für 2, 3, 5, 10 an, untersuchen Zahlen nach ihren Faktoren, in einfachen Fällen ohne digitale Mathematikwerkzeuge.	Ich kann zu einer Zahl kleiner als 100 alle Teiler angeben. Ich kann erklären, was eine Primzahl ist, und Beispiele angeben. Ich kann eine Zahl vollständig in ein Produkt von Primzahlen zerlegen. Ich kenne die Potenzschreibweise. Ich kann feststellen, ob eine Zahl durch 2, 3, 5 oder 10 teilbar ist, ohne die Division auszuführen. Ich kann zu zwei Zahlen den größten gemeinsamen Teiler (ggT) und das kleinste gemeinsame Vielfache (kgV) finden. Ich kann Zahlen erforschen, indem ich Beispiele untersuche, Vermutungen formulieren und sie überprüfe.	Auf dieser Seite sind Erklärungen und Videos zu Teilbarkeitsregeln: https://adi.dzlm.de/teilbarkeit
					Ganze Zahlen: Schwerpunkt negative Zahlen Zahlen darstellen Die Lernenden erkennen negative Zahlen als Alltagsphänomen, nutzen sinntragende Vorstellungen von ganzen Zahlen entsprechend der Verwendungsnotwendigkeit. mit ganzen Zahlen rechnen Die Lernenden rechnen mit ganzen Zahlen, die im täglichen Leben vorkommen, erklären Gesetze zum Rechnen mit negativen Zahlen.	Ich kann erklären, was negative Zahlen in Sachsituationen bedeuten. Ich kann positive und negative Zahlen auf der Zahlengeraden eintragen und ablesen. Ich kann positive und negative Zahlen der Größe nach vergleichen und der Größe nach ordnen. Ich kann Situationen (z. B. mit Geldfluss und Kontostand) mit positiven und negativen Zahlen beschreiben und dazu Bilder und Rechenaufgaben finden. Ich kann zu Additions- und Subtraktionsaufgaben mit negativen und positiven Zahlen Bilder zeichnen und Situationen angeben. Ich kann negative und positive Zahlen addieren und subtrahieren. Ich kann negative und positive Zahlen multiplizieren und dividieren.	Sprachliche Begleitung: „-5 Grad sind kälter als -1 Grad.“ „Wo sind die Schulden am größten?“ An der Zahlengeraden: Bezug zur 0 herstellen. Negative Zahlen als Spiegelbilder der positiven Zahlen, die am Nullpunkt gespiegelt sind. Z.B. ist -5 von der Null genauso weit entfernt wie 5. Hintergrundwissen und Unterrichtsmaterial: https://pikas-mi.dzlm.de/inhalte/negative-zahlen das Plus-Minus-Spiel: https://pikas-mi.dzlm.de/inhalte/negative-zahlen/unterricht/plus-minus-spiel
					Rationale Zahlen: Brüche darstellen, Bruchverständnis Die Lernenden deuten Brüche als Größen, Operatoren und Verhältnisse und nutzen das Grundprinzip des Kürzens und Erweiterns von Brüchen als Vergröbern bzw. Verfeinern der Einteilung, können Stammbrüche im Kontext des gerechten Verteilens eines Ganzen bestimmen und darstelle,. können mit Brüchen Anteile mehrerer Ganzer darstellen, bestimmen Anteile von Mengen mit Material, berechnen Anteile von Mengen. erläutern an Beispielen die verschiedenen Vorstellungen zum Bruchbegriff (insbesondere Teile eines oder mehrerer Ganzer, relative Anteile). können Brüche nutzen, um Verhältnisse anzugeben	Ich kann Anteile von einem Ganzen bestimmen und in einem Bild darstellen (Rechtecke, Kreise, Bruchstreifen). Ich kann Stammbrüche zu Verteilhandlungen bestimmen, z.B. 1 Kuchen für 4 Kinder. Ich kann Anteile von Mengen bestimmen und darstellen. Ich verstehe den Zusammenhang zwischen dem Teil, dem Anteil und dem Ganzen und weiß, dass ein Bruch den Anteil darstellt. Ich kann einen Anteil zu einem Ganzen ergänzen. Ich kann einfache Brüche (z.B. Mit einer 1 im Zähler) der Größe nach sortieren. Ich kann gleichwertige Anteile in Bildern und Situationen finden. Ich kann gleichwertige Brüche durch Erweitern und Kürzen finden. Ich kann Brüche gleichnamig machen. Ich kann Brüche vergleichen und der Größe nach ordnen. Ich kann Brüche nutzen, um Verhältnisse anzugeben.	Unterstützung zur Einführung der Bruchrechnung: Partibo-App: https://apps.apple.com/de/app/partibo/id1588419717 Padlet zur Partibo-App: https://padlet.com/Partibo/partibo-lehrkr-fte-9m06yvu9n4rrpqnm Mit dem Bruchstreifen lassen sich auch Anteile von Mengen darstellen. Bezug zu Prozenten: Wenn die Lernenden über Anteilsvorstellungen mit Brüchen verfügen, kann der Bezug zu Prozenten hergestellt werden, damit sie verstehen, dass Prozente kein inhaltlich neues Konzept sind, sondern eine andere Schreibweise für spezielle Brüche. Siehe dazu https://mathe-sicher-koennen.dzlm.de/mskfiles/uploads/docs/BausteinB1_L_Brueche_und_Prozente_verstehen.pdf Zum Finden gleichwertiger Brüche und zum Vergleichen von Brüchen ist die Streifentafel geeignet, auf der unterschiedlich unterteilte Bruchstreifen untereinander abgebildet sind. Streifentafel: https://mathe-sicher-koennen.dzlm.de/mskfiles/uploads/docs/BausteinB2_L_Gleichwertigkeit_verstehen.pdf
					Mit Brüchen rechnen Die Lernenden führen Grundrechenarten mit einfachen Brüchen aus (Kopfrechnen und schriftliche Rechenverfahren, Addition/Subtraktion).	Ich kann Brüche mit Hilfe eines Bildes addieren und subtrahieren. Ich kann Situationen, in denen Anteile zusammengefasst werden, durch Aufgaben beschreiben und umgekehrt. Ich kann Brüche durch Rechnen (ohne Bild) addieren und subtrahieren. Ich kann Brüche multiplizieren. Ich kann zu einer Multiplikation von Brüchen ein Bild zeichnen und eine Situation erfinden. Ich kann für Sachaufgaben mit Anteilen die richtige Rechenart finden. Ich kann Addition, Subtraktion und Multiplikation mit Brüchen sicher ausführen und kontrollieren. Ich kann mir zur Division von Brüchen eine Situation vorstellen und erklären, wie sie mit der Multiplikation zusammenhängt. Ich kann Divisionen mit Brüchen ausführen und erklären, wie man rechnet.	Wie bei dem Rechnen mit natürlichen Zahlen können vor der Einführung systematisierter Lösungsweisen des Rechnens mit Brüchen Rechnungen nach möglichen Vorgehensweisen sortiert werden (wie beim Zahlenblick). Durch eine flexible und aufgabenadäquate Vorgehensweise können Zahleigenschaften und Zahlbeziehungen erkannt und genutzt werden. Der Übergang zur systematischen Behandlung lässt sich mithilfe von Rechtecken realisieren (siehe Padberg & Wartha, 2017, S. 78ff).
					Prozente und Brüche – Die Lernenden deuten Prozentzahlen als andere Darstellungsformen für Brüche; – führen Umwandlungen zwischen Bruch und Prozentzahl durch, – können Hundertstel- und Zehntelbrüche in Prozent angeben, – können Brüche und Prozente ineinander umwandeln, – können ein Anteil als Bruch und als Prozentzahl darstellen. Prozent – Die Lernende verwenden Prozent- und Zinsrechnung vorstellungsbasiert (z. B. Prozentstreifen) und sachgerecht.	Prozente und Brüche Ich kann Hundertstel- und Zehntelbrüche in Prozent angeben. Ich kann Brüche und Prozente ineinander umwandeln. Ich kann einen Anteil als Bruch und als Prozentzahl darstellen. Ich kann Brüche und Prozente vergleichen und der Größe nach ordnen. Prozent Ich kann Prozente bestimmen und darstellen. Ich kann erklären, was eine Prozentzahl bedeutet, und diese in eine Dezimalzahl oder einen Bruch umwandeln. Ich kann erklären, was Prozentwert, Prozentsatz und Grundwert bedeuten. Ich kann erkennen, ob bei einer Aufgabe nach dem Prozentwert, dem Prozentsatz oder dem Grundwert gefragt ist. Ich kann Prozentaufgaben berechnen, indem ich Prozentstreifen, Minitabelle oder eine Rechnung verwende. Ich kann einfache Prozentaufgaben im Kopf berechnen.	Mit Bruchstreifen und Prozentstreifen kann der Zusammenhang zwischen Brüchen und Prozenten verdeutlicht werden. Siehe auch: https://mathe-sicher-koennen.dzlm.de/mskfiles/uploads/docs/BausteinB1_L_Brueche_und_Prozente_verstehen.pdf
					Rationale Zahlen: Dezimalbrüche Die Lernenden haben ein Stellenwertverständnis und können erklären, wie sich die Stellenwerttafel rechts von der Einerstelle fortsetzt, können zu Dezimalzahlen die Nachbarzahlen angeben und in Schritten zählen, können Dezimalzahlen vergleichen und der Größe nach ordnen. Die Lernenden deuten Dezimalzahlen und Prozentzahlen als andere Darstellungsformen für Brüche und stellen sie an der Zahlengerade dar; führen Umwandlungen zwischen Bruch, Dezimalzahl und Prozentzahl durch.	Ich kann Stellenwerte von Dezimalzahlen benennen und erklären, wie sich die Einheiten bündeln und entbündeln lassen. Ich kann Dezimalzahlen in der Stellenwerttafel darstellen. Ich kann Dezimalzahlen am Zahlenstrahl eintragen. Ich kann zu Dezimalzahlen Nachbarzahlen angeben und in Schritten zählen. Ich kann Dezimalzahlen vergleichen und der Größe nach ordnen. Ich kann Dezimalzahlen in Brüche und Prozente umwandeln und wieder zurück.	Die Lernenden haben häufig schon im Bereich Messen und Umgang mit Größen Erfahrungen mit Dezimalzahlen gesammelt. Die Bedeutungen des Kommas und der Nullen müssen thematisiert werden, da sonst Fehlvorstellungen entstehen können. Veranschaulichung und Material: Zahlenstrahl Erweiterte Stellentafel Stellenkarten Sprechweisen: Beispiel 2,63 Quasi-kardinal: Zwei 63 Hundertstel Formal: Zwei-Komma-sechs-drei
					Rationale Zahlen: Rechnen mit Dezimalbrüchen Die Lernenden können am Zahlenstrahl Rechenwege zur Addition und Subtraktion von Dezimalzahlen darstellen, können Dezimalzahlen schriftlich addieren und subtrahieren, können zwei Dezimalzahlen multiplizieren, Können die Multiplikation zweier Dezimalzahlen am Malkreuz erläutern, können zwei einfache Dezimalzahlen schriftlich multiplizieren oder schriftlich dividieren, können abschätzen, wie groß das Ergebnis beim Multiplizieren oder Dividieren zweier Dezimalzahlen ungefähr ist, können erkennen, wann die Division von Dezimalzahlen mit gleichen Ziffern zum gleichen Ergebnis führt, können mit meinem Taschenrechner Dezimalzahlen multiplizieren und dividieren und kann das Ergebnis überschlagen, um zu prüfen, ob es richtig sein kann, können mit gemischten Brüchen rechnen, indem sie sie in Dezimalzahlen umwandeln und dann rechnen, runden Zahlen dem Sachverhalt entsprechend sinnvoll.	Ich kann am Zahlenstrahl Rechenwege zur Addition und Subtraktion von Dezimalzahlen darstellen. Ich kann mit Hilfe der Stellenwerttafel Dezimalzahlen (schriftlich) addieren und subtrahieren. Ich kann Dezimalzahlen schriftlich addieren und subtrahieren. Ich kann zwei Dezimalzahlen multiplizieren. Ich kann die Multiplikation zweier Dezimalzahlen am Malkreuz erläutern. Ich kann zwei einfache Dezimalzahlen schriftlich multiplizieren oder schriftlich dividieren. Ich kann abschätzen, wie groß das Ergebnis beim Multiplizieren oder Dividieren zweier Dezimalzahlen ungefähr ist. Ich kann erkennen, wann die Division von Dezimalzahlen mit gleichen Ziffern zum gleichen Ergebnis führt. Ich kann mit meinem Taschenrechner Dezimalzahlen multiplizieren und dividieren und kann das Ergebnis überschlagen, um zu prüfen, ob es richtig sein kann. Ich kann mit gemischten Brüchen rechnen, indem ich sie in Dezimalzahlen umwandle und dann rechne. Ich kann Zahlen runden und mit ihnen rechnen, wenn der Sachverhalt es erfordert.	Rechenstrategien und -verfahren im Bereich der natürlichen Zahlen können auf das Rechnen mit Dezimalbrüchen übertragen werden. Zur Multiplikation eignet sich auch das Malkreuz.
					Rationale Zahlen allgemein Die Lernenden können für jede Schreibweise der rationale Zahlen typische Situationen angeben, für die man sie braucht, kennen die Fachwörter natürliche Zahl, ganze Zahl, Bruch, negative Zahl und rationale Zahl und können für jeden Zahlenbereich Beispiele und Gegenspiele angeben können alle Rechenarten (Addition, Subtraktion, Multiplikation und Division) für Dezimalzahlen sicher ausführen und kontrollieren.	Ich kann für jede Schreibweise rationale Zahlen typische Situationen angeben, für die man sie braucht. Ich kenne die Fachwörter natürliche Zahl, ganze Zahl, Bruch, negative Zahl und rationale Zahl und kann für jeden Zahlenbereich Beispiele und Gegenspiele angegeben. Ich kann alle Rechenarten (Addition, Subtraktion, Multiplikation und Division) für Dezimalzahlen sicher ausführen und kontrollieren.	Rationale Zahlen einfach erklärt: https://www.studienkreis.de/mathematik/rationale-zahlen/
					Wurzel Die Lernenden wählen, beschreiben und bewerten Vorgehensweisen und Verfahren, denen Algorithmen bzw. Kalküle zu Grunde liegen und führen diese aus, z. B. bei Wurzeln und Potenzen, implementieren ein algorithmisches Verfahren (z. B. Heron-Verfahren zur Bestimmung von Quadratwurzeln, Intervallschachtelung) mit digitalen Mathematikwerkzeugen, wenden das Radizieren als Umkehren des Potenzierens an; berechnen und überschlagen Quadratwurzeln einfacher Zahlen im Kopf, erläutern Potenzen und Wurzeln und berechnen einfache Potenzen und Wurzeln.	Ich kann erklären, was eine Wurzel ist. Ich kann Wurzeln durch Abschätzen ermitteln. Ich kann Wurzeln beliebig genau annähern und die Idee eines Annäherungsverfahrens erklären, z.B. mit dem Heron-Verfahren. Ich kann für die Wurzel einer natürlichen Zahl entscheiden, ob ihre Nachkommastellen abbrechen oder nicht. Ich beherrsche die Regeln für das Rechnen mit Wurzel. Ich kann mit einfachen Wurzeln von Bruchzahlen und Dezimalzahlen rechnen. Ich kann mit Wurzeln und Variablen rechnen.	Wurzeln ganzer Zahlen in drei Gruppen sortieren: Zahlen, deren Wurzel eine natürliche Zahl ist Zahlen, die keine Wurzel haben (negative Zahlen) Zahlen, deren Wurzel nicht als Bruch dargestellt werden kann
					Irrationale Zahlen Die Lernenden unterscheiden rationale und irrationale Zahlen. Reelle Zahlen Die Lernenden nutzen sinntragende Vorstellungen von reellen Zahlen (z. B. Vollständigkeit der Zahlengerade), beschreiben die Notwendigkeit von Zahlbereichserweiterungen von ℕ nach ℤ und ℚ sowie von ℚ nach ℝ an Beispielen.	Ich kann für eine Zahl sagen, ob sie rational, irrational, reell, ganz oder natürlich ist. Ich kann Beispiele für rationale, irrationale, reelle, ganze oder natürliche Zahlen nennen.	Erklärungen unter: https://mein-lernen.at/faktencheck-mathematik/rationale-vs-irrationale-zahlen-faktencheck-im-vergleich/
					Kombinatorik Die Lernenden bestimmen Anzahlen auf systematische Weise mit verschiedenen Strategien, führen in konkreten Situationen systematische Zählprinzipien aus (z. B. Anzahl Händeschütteln, wenn man jeder Person die Hand gibt).	ich kann Möglichkeiten geschickt zählen mit der Strategie „systematisches Aufschreiben von Listen“. Ich kann Möglichkeiten geschickt zählen mit der Strategie „systematisches Zeichnen von Baumdiagrammen“. Ich kann Möglichkeiten geschickt zählen mit der Strategie „in Schritten zählen und rechnen“.H66	Erklärungen zur Produkt- und Summenregel sind auf dieser Seite: https://adi.dzlm.de/kombinatorik/produktregel-der-kombinatorik Zwei Kategorien von Aufgaben: Die Elemente einer Menge sollen auf verschiedene Weise angeordnet werden. Aus einer oder mehreren Mengen sollen Objekte ausgewählt werden: mit oder ohne Beachtung der Reihenfolge

Zum Inhaltsverzeichnis zurück

Tabelle 3.2: Größen und Messen

Abkürzungen Tabellen: b = basal | e = elementar | p = primär | s = sekundär


					Teilbereich: Größen und Messen (Sachrechnen) Der Teilbereich Größen und Messen verbindet die Bereiche Zahlen und Operationen mit Raum und Form. Anwendung finden Größen in Sachsituationen. Daher ist der Bereich eng mit dem Sachrechnen verbunden. Für die Entwicklungsorientierung ist von einem linearen Prozess abzusehen, da die Lernenden unsystematische und vielfältige Vorerfahrungen aus dem Alltag mitbringen, die dem bewussten Umgang zugänglich gemacht werden sollen (Franke/Ruwisch 2010, S. 178). Dennoch ist es hilfreich, sich den jeweiligen Abstraktionsprozess zu verdeutlichen.
					Muster, Strukturen und funktionale Zusammenhänge Hierbei handelt es sich um einen übergeordneten Kompetenzbereich, der sich mit den prozessbezogenen Kompetenzen überschneidet. Lernende entdecken bei der Auseinandersetzung mit mathematischen Mustern und Darstellungen mathematisch relevante Strukturen in allen inhaltsbezogenen Bereichen. Sie erkunden fachlich fundiert mathematische Beziehungen und Gesetzmäßigkeiten zwischen Zahlen, Formen und Größen sowie deren Darstellungen und Eigenschaften, die sie erkennen, beschreiben und darstellen. Dazu gehören z.B. funktionale Beziehungen, Sortierungen, Ordnungen. Muster, Strukturen und funktionale Zusammenhänge im Bereich Größen und Messen „Lernende kennen Standardeinheiten (zu Geldwerten, Längen, Zeitspannen, Hohlmaßen und zur Masse) und setzen diese im jeweiligen Größenbereich zueinander in Beziehung“ (KMK 2022, S. 15).			Pädagogische Angebote bieten strukturierte Zugänge beim Vergleichen von Längen, Zeitspannen, Gewichten und der Nutzung von Maßeinheiten beim Lösen von Sachaufgaben. Durch Standardeinheiten werden gleiche Größen erkannt und Unterschiede (mehr – weniger, länger – kürzer, leichter – schwerer, voll - leer usw.) in ihren funktionalen Beziehungen thematisiert. Muster bei der Nutzung von Stützpunktvorstellungen (Anwendung der Maßeinheiten, Schätzen, Messen) tragen zu Lösung von Sachfragen bei.
b	e	p	s	ILZ	Stufe in Erwachsenensprache	Stufe in Kindersprache	Lernbausteine
				1a	Sinnliche Welterkundung Allgemein-mathematische Kompetenzen basieren auf einer aktiv-entdeckenden Auseinandersetzung durch Zufallshandlungen mit Dingen/Gegenständen Inhaltsbezogene mathematische Vorerfahrungen Die Lernenden handeln zufällig in ihrem Körper- und Nahfeld. Durch die Komplexität der Situation können sie basale Erfahrungen in den sich überschneidenden Kompetenzbereichen machen. Die Gestaltung des Nah- und Greiffelds ermöglicht ihnen das Lernen durch Berühren, Bewegen, Beobachten interessanter Eigenschaften und Merkmale: Raumerfahrungen durch Lagerungsorte (Rollstuhl, Little Room usw.), Raumbegrenzungen, räumliche Anordnung von Dingen (oben- unten, vorne – hinten, innen – außen) sind bedeutsam für den Kompetenzbereich Raum und Form (RuF), basale Vorerfahrungen durch regelmäßige und wiederholte zeitliche Abläufe und räumliche Angebote in den Kompetenzbereichen Muster und Strukturen/ Strukturen und funktionaler Zusammenhang (SufZ) sowie Daten, Häufigkeit und Wahrscheinlichkeit/Daten und Zufall (DuZ), sinnliche Erfahrungen durch die Beschaffenheit von Dingen (einschließlich Geruch und Geschmack) mit weiteren unterschiedlichen Eigenschaften und Merkmalen (hart – weich, farbig, glatt, laut – leise, hell – dunkel usw.) Formen (rund – eckig) sind bedeutsam für den Kompetenzbereich Raum und Form (RuF), Erfahrungen bei den Zufallshandlungen mit Gewicht, Größe, Entfernung (groß – klein, leicht – schwer, nah – weit) sind bedeutsam für den Kompetenzbereich Größen und Messen (GuM) Die benannten Erfahrungen ermöglichen die Entwicklung der Fähigkeit, Dinge grundsätzlich zu unterscheiden. Das ist wiederum eine Voraussetzung für das Bilden von Mengen (Sortieren) im Kompetenzbereich Zahl und Operation (ZuO)	Ich kann, was um mich geschieht hören, sehen, spüren, riechen, schmecken, fühlen. Ich kann die Dinge, die ich zufällig ergreife, berühren, belecken und in Bewegung bringen. Dabei erfahre ich, dass sich Gegenstände und Materialien unterschiedlich anfühlen. Ich beginne, ganz bestimmte Personen, Gegenstände und Materialien, Muster, Formen zu bevorzugen und kann dies durch Zuwendung, Wiederholung, durch Mimik, Gestik und durch Laute zum Ausdruck bringen.	Gestaltung des Nah- und Greiffelds: Materialien und Gegenstände sind im Nah- und Greiffeld angebracht, • die leicht berührt und bewegt werden können • die Geräusche oder Lichteffekte auslösen • die kontrastreiche Muster und Farben haben • die aus unterschiedlichen Formen und Materialen bestehen Handlungen werden von Bezugspersonen und anderen Lernenden beobachtet und im Dialog gespiegelt. Materialien, die zu aktiven Wiederholungen anregen, werden gezielt angeboten und durch weitere, mit ähnlichen Eigenschaften ergänzt. ...
				1b	Welterkundung durch unspezifisches Operieren Aktive Wiederholungen erweitern die allgemein-mathematische Kompetenzen durch die aktiv-entdeckenden Auseinandersetzung mit Dingen/Gegenständen Inhaltsbezogene mathematische Vorerfahrungen Interessante Effekte durch Dinge und Materialien im Körper-, Nah- und Greiffeld werden von den Lernenden aktiv wiederholt und die inhaltsbezogenen Vorerfahrungen zu den Kompetenzbereichen (SufZ, RuF, GuM, ZuO, DHuW s.o.) können sich jeweils festigen und erweitern. Dinge/Gegenstände werden mit dem Mund, den Händen oder Füßen erkundet (Berühren, Klopfen, Werfen usw.). Erreichbare Materialien und Dinge ermöglichen so die aktive Wahrnehmung und zunehmende Unterscheidung von Gegenständen und deren Eigenschaften: Länge, Gewicht, Größe, Beschaffenheit, Form, Farbe, Klangeffekte, Geruch, Geschmack usw.	Ich kann Bewegungen, die es mir ermöglichen, für mich bedeutsame Dinge zu erreichen oder Effekte herbeizuführen, aktiv wiederholen. Ich kann diese Dinge mit dem Mund, den Händen und den Füßen durch Berühren, Klopfen, Werfen usw. immer genauer erkunden und so Größe, Beschaffenheit, Form, Farbe, Klangeffekte, Geruch, Geschmack usw. wahrnehmen. Ich erfahre durch aktive Wiederholungen, dass sich die Gegenstände und Dinge in meiner Umgebung unterschiedlich anfühlen, dass sie unterschiedlich aussehen, riechen, schmecken oder klingen.	Gestaltung des Nah- und Greiffelds: Bevorzugte Gegenstände, Materialien werden so angebracht, dass sie erreichbar sind aktive Wiederholungen ermöglichen und Zeit für die selbsttätige Erkundung zur Verfügung steht. z.B. Lagerung in Rückenlage auf einem Resonanzbrett, auf dem Materialien getastet werden können. Das Resonanzbrett verstärkt akustische Effekte und animiert zur Erkundung Im Stehständer werden Materialien im Greiffeld angebracht, die durch die aktiven Wiederholungen Spür-, Seh- und Höreindrücke auslösen und die Aufmerksamkeit anregen.
				1c	Welterkundung durch spezifisches Hantieren Spezifisches Hantieren erweitert die allgemein-mathematischen Kompetenzen durch die gezieltere aktiv-entdeckende Auseinandersetzung mit (nichtzahligen und zahligen) Dingen/Gegenständen und deren Funktion Inhaltsbezogene mathematische Vorerfahrungen Die Lernenden erkunden gezielt Dinge/Gegenstände und Materialien in ihrer unmittelbaren Umgebung und wenden als bewährt erfahrene Handlungsschemata (Lecken, Beißen, Klopfen, Werfen, Fallenlassen usw.) an. Auf diese Weise erfahren sie deren unterschiedlichen Eigenschaften (GuM, ZuO), deren räumliche Anordnungen (RuF) und die Veränderbarkeit von Mengen (Teile-Ganzes-Schema) (ZuO) Die funktionsbezogene Nutzung ist noch nicht erschlossen. Als bewährt erfahrene Handlungsschemata werden auf Neues angewendet (Lecken, Beißen, Klopfen, Werfen, Fallenlassen usw.). Die Unterschiede in den Dingen/Gegenständen und Materialien führen zu neuen Erfahrungen. Allgemeine mathematische Vorerfahrungen (Kommunizieren) Durch die Beobachtung anderer Menschen und im Dialog werden die Handlungen verbal gespiegelt und die funktionsbezogene Nutzung von Gegenständen angebahnt.	Ich kann Materialien und Gegenstände mit dem Mund, den Augen und den Händen gezielter erkunden. Ich kann die dabei erprobten Handlungen (Lecken, Beißen, Fallenlassen…) zur Erkundung noch unbekannter Gegenstände anwenden. Ich kann beobachten, wie andere Menschen mit den Gegenständen umgehen und beginne dadurch wahrzunehmen, wie diese genutzt werden. Ich lerne, dass nicht alle meine erprobten Handlungsweisen für jeden Gegenstand geeignet sind. Ich beginne, Gegenstände durch bestimmte Merkmale als zueinander zugehörig wahrzunehmen.	Gestaltung des Handlungsfelds: Der Arbeitsbereich ist so zu gestalten, dass mit den darin erreichbaren Gegenständen hantiert werden kann (abgegrenzter räumlicher Bereich, Multifunktionstisch MFA-Tisch, Tastbretter, Materialkisten). Für das zunächst noch nicht an den Funktionen orientierte Erkunden durch Lecken, Beißen, Klopfen, Werfen usw. müssen Gegenstände und Materialien robust und stabil sein Dadurch wird und ermöglicht, dass die unterschiedlichen Eigenschaften untersucht werden können. Materialkisten (GuM, ZuO) und verschiedene Behältnisse (RuF) werden zeitlich und räumlich verlässlich zur Verfügung gestellt (DHuW, RuF, SufZ) . Sie können ausgeleert und eingeräumt werden können. Mengen können umgefüllt, verändert und sortiert werden (MFA-Tisch n. Nielsen) (ZuO, SufZ, RuF). Tastbretter mit daran befestigtem Material ermöglichen eine intensive Beschäftigung mit deren Eigenschaften (RuF, GuM, SufZ). Kommunizieren Andere Menschen spiegeln diese Handlungen und zeigen vorbildhaft die funktionsbezogene Nutzung von Gegenständen. Die Nachahmungsfähigkeit wird dadurch angeregt.
					Übergang zur elementaren Stufe: Mathematische Basiskompetenzen Vorzahlige Handlungen werden mit zahligem Handeln verbunden. Zahlwörter und Zahlen gewinnen im Alltag (zwei Äpfel, drei Brötchen), in Fingerspielen, Liedern und Geschichten und als Abbildungen sowie Mengenwissen (viel – wenig) an Bedeutung (bedeutsam für den Kompetenzbereich ZuO). Eigenschaften von Dingen werden verglichen (groß – klein, schwer – leicht, lang-kurz, kalt-heiß) (bedeutsam für den Kompetenzbereich GuM), räumliche und strukturierte Anordnungen (bedeutsam für den Kompetenzbereich MSufZ) dienen der Orientierung (oben-unten, hinten-vorne, aufgereiht, nebeneinander), die Gestalt der Dinge wird im Handeln erfahren (rund – eckig) (bedeutsam für den Kompetenzbereich RuF). Zeitliche Abläufe (erst – dann, gleich – später, Tage, Stunden, Minuten)) werden in sich wiederholenden Strukturen erfahren (bedeutsam auch für die Kompetenzbereiche GuM, DuZ, MSufZ). Prozessbezogene Kompetenzen In Alltags- und Sachsituationen werden zur Klärung oder Problemlösung mathematische Beschreibungen wahrgenommen. Bei Mengenvergleiche werden Begriffe aus der Mathematiksprache gehört und angewendet (Darstellen und Kommunizieren ). Bei Reihenfolgen wird auf Ordnungszahlen Bezug genommen (1., 2., 3. sein). Strukturierte Darstellungen werden zur Orientierung angewendet.	Ich beginne, Zahlwörter und Zahlen im Alltag wahrzunehmen. Ich interessiere mich für Zahlen und Ziffern im Alltag, in Liedern und Geschichten. Ich handele mit Gegenständen in meiner Umgebung und beginne sie zu vergleichen und zu unterscheiden, ob sie groß oder klein, kurz oder lang, schwer oder leicht sind. Wenn ich mir eine Ansammlung von Gegenständen anschaue, kann ich einschätzen, ob es viel oder wenig Gegenstände sind. Ich kann sagen, wo sich die Dinge befinden (vorne, hinten…) und wie sie angeordnet sind (nebeneinander, übereinander usw.). Ich weiß, dass bestimmte Ereignisse jeden Tag, jede Woche zur gleichen Zeit stattfinden und kann darüber berichten. Ich habe eine Vorstellung dazu entwickelt, was es bedeutet, wenn ich einen Tag oder wenige Minuten auf etwas warten soll. Ich kann mich mit anderen darüber austauschen, ob alle gleich viel Dinge gesammelt haben oder nicht. Ich kann zeigen, woran ich das erkennen kann. Wenn wir einen Wettlauf machen, kann ich gemeinsam mit den anderen feststellen, wer 1., 2., oder 3. geworden ist.	Inhalts- und prozessbezogene Kompetenzen Bezugspersonen thematisieren zahliges Handeln in Alltagszusammenhängen. Dabei werden die verschiedenen Bedeutungszusammenhänge bei der Verwendung von Zahlwörtern und Ziffern erklärt (Zahlen zum Abzählen, Zahlen zum Messen, Zahlen zum Bezeichnen (Haus-Nr., Auto-Nr.). Beispiele unter PIKAS Mathe ein Kinderspiel Literatur: (Koch u.a.2020) Die Lehrkraft beschreibt konkrete Handlungen im Alltag (bedeutsam für: GuM, DuZ, MSufZ) mit Mathematiksprache und regt zum Entdecken von mathematischen Handlungen an. Sie verwendet vorbildhaft Begriffe aus der Mathematiksprache (Darstellen, Kommunizieren): Zahlen, viel – wenig, mehr – wenige, um eins mehr, sind zusammen usw. Beispiele in: PIKAS: Fachwortschatz Mathematik Sie verwendet vorbildhaft Begriffe aus der Mathematiksprache (Darstellen, Kommunizieren): Zahlen, viel – wenig, mehr – wenige, um eins mehr, sind zusammen usw. Beispiele in: PIKAS: Fachwortschatz Mathematik Sie verwendet vorbildhaft Begriffe aus der Mathematiksprache (Darstellen, Kommunizieren): Zahlen, viel – wenig, mehr – wenige, um eins mehr, sind zusammen usw. Beispiele in: PIKAS: Fachwortschatz Mathematik
					Sammeln erster Größenvergleichs- und Messerfahrungen als Grundstein eines umfassenden Größenkonzept Erfahrungen in Sach-, Spiel- und Alltagssituationen Die Lernenden beginnen Unterschiede in den Eigenschaften von Dingen, Personen, Entfernungen, Dauer usw. wahrzunehmen. Beim Vergleichen, Ordnen und Sortieren der Eigenschaften von Gegenständen werden qualitative Größenbezeichnungen verwendet (größer- kleiner, länger – kürzer, schwerer – leichter, höher – tiefer, mehr – weniger usw.). Lernende erfahren, dass Größen wie Länge, Gewicht, Zeit und Geldwerte bedeutsam sind und durch Maßzahlen bezeichnet werden. Lernende verfügen über unterschiedliche und unsystematische Vorerfahrungen, die in den folgenden Phasen des Umgangs mit Größen erweitert werden. Lernende entwickeln erste Größenvorstellungen durch vielfältige Aktivitäten mit dem Vergleichen der Länge, des Gewichts und des Volumens von Gegenständen. Erste Vergleichs- und Messerfahrungen (Bereiche: Längen, Flächen, Volumen, Zeit, Gewichte) bilden den Grundstein für den späteteren Aufbau eines umfassenden Größenkonzepts. Die Lernenden erfahren, dass eine Größenangabe immer aus einer Maßzahl und einer Maßeinheit besteht. Die Maßeinheit kann eine individuelle (z.B. 10 Schritte) oder eine standardisierte Größe (2 Meter) sein.	Ich weiß, dass Dinge/Menschen größer oder kleiner, schwerer oder leichter als andere sind. Ich kann beim Einkaufenspielen ansagen, was und welche Menge ich haben will und bekomme das Gewünschte gegen Geld. Was die Geldscheine genau bedeuten, weiß ich noch nicht. Wir können erfahren, wer größer ist, wenn wir uns Rücken an Rücken stellen. Ich kann entscheiden, was länger und was kürzer ist, in dem ich Dinge nebeneinander lege. Ich kann prüfen, welcher Stein schwerer und welcher leichter ist, indem ich beide hochheben.	Inhaltsbezogene Kompetenzen Lehrkräfte thematisieren in Alltagshandlungen die messbaren Eigenschaften von Dingen oder Personen. Länge und regen zum direkten oder indirekten Vergleich an: Länge: Wie groß ist etwas oder jemand? Was oder wer ist größer – kleiner, länger - kürzer? Wie können wir das feststellen? Gewicht: Wie schwer ist etwas, was ist schwerer, was ist leichter? Wie können wir das feststellen? Wie viel wiegt etwas (z.B. Lebensmittel, Gegenstände)? Volumen/Rauminhalt: Wie viel passt in ein Gefäß? In welches Gefäß passt mehr? Wie können wir das feststellen?
					Indirekte und direkte Vergleiche Länge: Die Lernenden erkennen, dass etwas lang, kurz oder länger und kürzer sein kann (Beziehung zum Kompetenzbereich RuF) oder dass sich etwas in der Nähe oder in einer bestimmten Entfernung befindet. Die Lernenden erfahren, dass Längen direkt verglichen werden können: Die einfachste Form des Messens ist der direkte Vergleich (Rücken an Rücken stellen, um die Körpergröße zu vergleichen). Kann es z.B. nicht möglich sein, Weglängen direkt zu vergleichen, beginnen die Lernenden zu verstehen, dass dazu Mittler, bzw. Repräsentanten (willkürliche, nicht standardisierte Hilfsmittel) wie Schritte, Stöcke oder Seile zum indirekten Vergleich genutzt werden können. Ergänzend lernen sie Lineale, Maßbänder oder Maßstäbe als standardisierte Messinstrumente anwenden.	Ich kann auch die Länge von einem Ding mit einem Faden messen und den überstehenden Faden abschneiden. Dieses Fadenstück kann ich dann überall anlegen und so prüfen, was gleich lang, kürzer oder länger ist. Ich kann mitteilen, wie lang der Weg von der Haustür bis zum Auto ist, wenn ich meine Schritte auf dem Weg dahin zähle und die Schrittzahl ansage. Ich schreite verschiedene Strecken ab und vergleiche durch die Anzahl von Schritten, welche Strecke länger oder kürzer ist. Ich kann die Länge eines Bildes mit Hilfe von Handspannen angeben und so die Länge von verschiedenen Bildern vergleichen. Ich kann an der Messlatte zu meiner Körperlänge zunächst die Zahl als Abbildung erkennen und das Zahlwort als Bezeichnung nennen.	Indirekter Längenvergleich: es werden Seile, Stöcke zur Verfügung gestellt, wenn der direkte Vergleich nicht möglich ist. Werden Schritte genutzt, kann anschließend standardisiert gemessen werden, da Schritte sehr unterschiedlich lang sein können.
					Gewicht: Lernende machen beim Transport von Gegenständen und im hauswirtschaftlichen Bereich Erfahrungen mit Gewichten. Sie lernen dazu Hilfsmittel (z.B. Tassen, Teelöffel) und standardisierte Messinstrumente kennen (Waagen, Messbecher).	Ich kann ausprobieren, ob etwas schwer oder leicht ist, indem ich es anhebe und vergleiche. Ich weiß, dass ich Mengen abwiegen kann. Ich kann z.B. die Maßangabe 200g zum Abwiegen nutzen, indem ich die abgebildete Zahl auf dem Rezept durch Hinzufügen auf der Waage wiedererkenne. Ich kann Zahlen auf einem Rezept erkennen und mit der Waage, dem Messbecher eine Menge abwiegen, die mit dieser Zahl übereinstimmt	Gewicht: Beim Transport von Gegenständen wird das Gewicht thematisiert, was fühlt sich schwerer, leichter an. Die Einschätzungen werden mit Hilfe standardisierter Messinstrumente (Waagen) kontrolliert.
					Volumen/Rauminhalt: Die Lernenden können z.B. flüssige Mengen vergleichen, indem sie mit verschiedenen Bechern, Kannen, Flaschen usw. Flüssigkeiten einfüllen, umfüllen oder verteilen. Sie messen indirekt mit Bechern oder nutzen standardisierte Messinstrumente wie z.B. Messbecher.	Ich kann feststellen, wie viel Flüssigkeit in eine Kanne passt, indem ich zähle, wie viele volle Becher ich benötige, um sie zu füllen. Ich vergleiche, in welchem Gefäß mehr oder weniger Flüssigkeit ist, indem ich zum Umschütten ein Glas oder einen Becher verwende und feststelle in welches Gefäß mehr oder weniger Glas- oder Becherfüllungen passen.	Volumen/Rauminhalt Kannen, Flaschen und Becher zum Volumenvergleich werden zur Verfügung gestellt. Alltagsfragen entwickeln: z.B. wie viele Becher können wir mit einer Kanne füllen?
					Geld: Im Alltag (z.B. beim Einkaufen) erleben die Lernenden die Bedeutung von Größenangaben und Geld. Sie ahmen den Umgang damit in Rollenspielen (Einkaufen, Handwerkerspiel…) nach und sammeln so Vorerfahrungen zum Maßzahlaspekt und zu Größenangaben. Beispiele in: Ministerium für Kultur, Jugend u. Sport Baden Württenberg 2022, S. 28	Ich weiß, dass man Geld zum Einkaufen braucht und dass es unterschiedliche Geldscheine und unterschiedliche Geldmünzen gibt. Ich kann die Geldscheine und die Münzen auf Grund ihres Aussehens sortieren, weiß aber noch nicht, welcher Schein mehr oder weniger im Vergleich zu anderen Scheinen oder Münzen wert sind.	Geld: Einkaufsanlässe, Klassenkasse usw. oder Rollenspiele zum Einkauf werden genutzt. Münzen werden verglichen usw. Ministerium für Kultur, Jugend u. Sport Baden-Württenberg (Hrsg.) (2022, S. 20 ff.
					Zeit: Lernende sind im Alltag mit Zeitabläufen konfrontiert. Sie benötigen Ablaufpläne mit Zeiteinheiten, die durch Sanduhren, Timer oder Uhren (digital oder analog) visualisiert werden.	Ich weiß, dass ich durch Sanduhren, Timer oder Abbildungen von Uhrzeiten überschauen kann, wie lange etwas daurt.	Zeit: Auf Tages-, Stunden oder Phasenabläufe werden Zeitangaben visualisiert und mit der Verwendung von Sanduhren, Timer oder Uhren in Beziehung gebracht. Zeitpläne werden mit Uhrzeiten in Verbindung gebracht. Sanduhren verdeutlichen Zeitabläufe.
					Messgeräte werden bereits kennen gelernt, wenngleich sie von den Lernenden selbst noch nicht sachgerecht gehandhabt werden. Zunächst können Lernende Maßzahlen „ablesen“: Zahlen auf Verpackungen wie 100g, I Liter usw. werden im Alltag als Ganzheiten abgespeichert und wiedererkannt. Kochrezepte können ohne Anzahlverständnis durch die auf Messgeräten abgebildeten Zahlen umgesetzt werden. Die regelmäßige Anordnung der Zahlen (Beziehung zum Kompetenzbereich MSufZ) bildet das Maß ab. Bei der Angabe zu Körpergröße werden Dezimalzahlen ohne Dezimalzahlverständnis als Bezeichnung genutzt („Ich bin 1 Meter 20 groß“). Hier handelt es sich noch um unverbundenes Wissen. Realistische Vorstellungen zu den Größenangaben bedürfen des Vergleichens von Repräsentanten und des Umgangs mit Messgeräten. Geldwerte können durch die Zuordnung zu bestimmten Münzen oder Scheinen als Abbildungen erfasst werden. Eine 50-Cent-Münze oder ein 5 Euro-Schein werden erkannt und beim Einkauf verwendet, ohne dass die Werte und die Beziehungen der Werte untereinander verstanden sind.	Ich weiß, dass es Instrumente gibt, mit denen man die Länge, das Gewicht, das Fassungsvermögen exakt messen kann und dass man bestimmte Maßeinheiten braucht, um das Gemessene zu benennen. Von einigen kenne ich schon den Namen, z.B. weiß ich, dass man die Länge von Gegenständen oder Entfernungen in Meter und Zentimeter angibt.	Messgeräte (Messlatte, Waagen, Messbecher) werden in Sachsituationen als Alternative zu den individuellen Messhilfen angeboten und in ihrer Anwendung demonstriert.
					Prozessbezogene Kompetenzen Die Lernenden interessieren sich für Größen in Alltagszusammenhängen, entwickeln Fragestellungen, die durch die Nutzung von Messgeräten gelöst werden können und tauschen sich darüber aus (kommunizieren). Sie modellieren Rechenwege, argumentieren darüber und stellen ihre Ergebnisse dar.	Ich kann mit anderen darüber reden, wer größer oder kleiner ist und gemeinsam entwickeln wir Vorgehensweisen, wie wir das feststellen könnten (Rücken an Rücken stellen, Striche im Türbogen einzeichnen…) und probieren sie aus. Ich interessiere mich für Gewichte und kann mit Anderen beraten, wie wir erkunden könnten, was schwerer und was leichter ist. Wir versuchen dann gemeinsam Fragen zu beantworten, die wir uns stellen, z.B. wer den schwersten Rucksack hat oder ob unsere Stiefel gleich schwer sind.	Prozessbezogene Kompetenzen Fragestellungen zu Größen, zum Vergleich von Objekten, der Nutzung von individuellen, nicht standardisierten und von standardisierten Messeräten werden in Alltagszusammenhängen kommuniziert. Rechenwege werden modelliert, beschrieben und argumentiert. Ergebnisse werden dargestellt.
					Weiterentwicklung des Größenkonzepts und sachgerechte Nutzung von Messinstrumenten Die Lernenden verstehen, dass Messungen dazu dienen, Größen bestimmen, vergleichen und ordnen zu können. Die Lernenden erkennen, dass dazu standardisierte Messinstrumente genutzt werden müssen. Die Auswahl von Messinstrumenten und deren Anwendung bei der Nutzung von Maßeinheiten führt zu tragfähigen Größenvorstellungen von Maßzahlen. Grundgrößen sind Länge, Masse (Gewicht) und Zeit. Systematisches Vergleichen von Objekten mit Hilfe von Repräsentanten (Entwicklung von Stützpunktvorstellungen) Lernende haben bereits Erfahrungen mit dem direkten Vergleichen gemacht, um Unterschiede im Bereich der Länge, des Gewichts, des Volumens zu erkunden. Daran anknüpfend setzten die Lernenden über das direkte Vergleichen zweier Objekte deren jeweiligen Größen (Maßeinheiten) in Beziehung zueinander: kürzer als, so lang wie, schwerer als usw. Sie entwickeln auf diese Weise das Grundwissen darüber, dass Dinge gleiche Maße haben (Äquivalenzrelation: gleiche Größe) oder dass deren Maße in einer gewissen Ordnung zueinanderstehen (Ordnungsrelation: länger-kürzer als, leichter – schwerer als usw.). Über realistische Beispiele können sie lernen, sich eine Größe vorzustellen (Stützpunktvorstellungen). Solche Bezugsgrößen stellen die Grundlage dafür da, sich bei der Lösung von Sachproblemen an genaue Maße anzunähern, die dann durch die passenden Messgeräte ermittelt werden können. Lernende benötigen die Stützpunktvorstellungen als Grundlage für die erste Umrechnung von Maßeinheiten (von cm in m, von kg in g usw.).	Ich kann Gegenstände, Strecken usw. mit selbstausgedachten „Messinstrumenten“ vergleichen und sagen, was länger, kürzer, schwerer, leichter usw. ist. Ich weiß allerdings auch schon, dass ganz genaue Angaben zur Länge, zum Gewicht, zum Fassungsvermögen von Objekten nur mit Hilfe von geeigneten Messinstrumenten möglich ist. Ich weiß, dass das Ergebnis einer Messung durch eine Zahl (Maßzahl) und der Angabe der Maßeinheit (z.B. m, cm, kg, g) angegeben wird. Auf diese Maßeinheiten haben sich die Menschen geeinigt und es ist eindeutig festgelegt, was sie bedeuten.	Inhaltsbezogene Kompetenzen Lehrkräfte ermitteln die unterschiedlichen und unsystematischen Vorerfahrungen der Lernenden (Franke/Ruwisch 2010, S. 178) und weisen in lebenspraktischen Bezügen und Alltagshandlungen auf mögliche zu verwendende Maßeinheiten hin. Sie stellen Messgeräte oder Messinstrumente vor, besprechen Maßangaben usw. (fächerübergreifender Unterricht (NaWi, Sachunterricht, Hauswirtschaft usw. Sachrechnen) Stützpunktvorstellungen werden aufgebaut bzw. weiter ausgebaut: Das sind realistische, alltagstaugliche Vorstellungen zu Größen und Größenbegriffen. Als Vergleichswerte unterstützen sie die Lernenden, sich die Größen der Maßeinheit realistisch vorzustellen und zu merken. Als Vorstellungshilfen ermöglichen sie den Lernenden, unbekannte Größen über Vergleiche mit ihnen zu erahnen (vgl. Reuter/Neubert 2010, S. 4 ff.) Literaturhinweis zur Diagnostik: Wollring u.a. 2011 EMBI Größen und Messen PRIMAKOM: Größen und Messen - Sachrechnen PIKAS Größen & Messen https://pikas.dzlm.de/unterricht/größen-und-messen Phasen der Erarbeitung des Umgangs mit Größen finden nicht immer linear statt, dienen aber der Orientierung für die Planung des Unterrichts (Franke/Ruwisch 2010, S. 184). Angebote zum Sammeln von Größenerfahrungen im Alltag sowie Austausch darüber führen zum forschenden Umgang mit Größen. Ein Größenbuch kann angelegt werden, in dem diese festgehalten werden können. Beispiel für das Anlegen eines Größenbuches (Primakom) Weitere Anregungen PRIMAKOM: Größenbegriff
					Länge: Lernende erfahren, dass durch selbstgewählte Maßeinheiten (Schritte, Handspannen, Stäbchen o.ä. kein objektiver Größenvergleich möglich ist. Sie verstehen, dass die objektive Größe nur durch standardisierte Messinstrumente (Lineal, Zentimetermaß, Maßstab, Messlatte usw.) festgestellt werden kann. Die Lernenden kennen die dazu die passenden Maßeinheiten cm, m und wenden sie zum Vergleich an. Stützpunktvorstellungen (Türhöhe 2 m, Abstand zwischen zwei Kästchen auf dem Lineal 1 cm usw.) dienen der Längenorientierung und können als Grundlage für Schätzungen dienen.	Ich weiß, dass eine Tür ungefähr 2 m hoch ist. Dazu habe ich eine Vorstellung entwickelt. Diese hilft mir zu schätzen, wie hoch beispielsweise ein Haus ist.	Länge: Lernende vergleichen ihre Körpermaße, gebaute oder gelegte Dinge werden nebeneinander angeordnet und verglichen (Türme aus Bausteinen, Strecken durch Aneinanderlegen). Entfernungen werden gemessen. Körpereigene Längen (Fuß, Schritt, Handspanne) bieten sich als handlungsorientierte Zugänge an. Wegen ihrer Ungenauigkeit werden anschließend genaue Messungen mit standardisierten Messgeräten durchgeführt. PIKAS Längenbegriff: Literatur: Franke/Ruwisch 2010, S. 204-210).
					Flächen: Die Lernenden erkennen Flächengrenzen zunächst z.B. durch die Länge und Breite von Tischen, Teppichen usw. und den damit zur Verfügung stehenden Platz. Flächenvergleiche können durch Übereinanderlegen oder indirekt durch Auslegen mit selbstgewählten Einheiten durchgeführt werden (Beziehung zum Kompetenzbereich RuF).	Ich kann Papierplätter, die Größe von Decken usw. vergleichen indem ich sie sorgfältig übereinander lege und dann sehe, ob etwas übersteht. Wenn etwas übersteht, weiß ich, dass dieses Blatt, diese Decke usw. größer ist.	Flächen: Zur Verfügung stehende Bereiche werden benannt. „Du kannst den Tisch nutzen, auf dem Teppich arbeiten!“ usw. Es geht hierbei noch nicht um die Berechnung von Flächen. Diese setzt die Kompetenz Multiplikation voraus (Maßeinheiten: cm2, m2): (-> RuF, ZuO)
					Gewichte: Die Lernenden erfahren im Spiel und Alltag, dass Dinge schwer, leicht oder schwerer und leichter sein können. Für die Anwendung der Maßeinheiten z.B. beim Vergleich von Koch- oder Backzutaten werden als standardisierte Messgeräte Waagen genutzt. Die Maßeinheiten kg, g werden in Maßzahlen abgebildet und können verglichen, verringert oder erhöht werden (Beziehung zum Kompetenzbereich ZuO). Stützpunktvorstellungen sind hier z.B. das eigene Gewicht, Gewicht des Schulranzens oder z.B. 100g für eine Tafel Schokolade usw.	Ich weiß, dass eine Tüte Mehl 1 kg schwer ist. Weil ich so eine Tüte schon oft in der Hand hatte, habe ich eine Vorstellung entwickelt, wie sich 1kg anfühlt und kann durch Vergleich schätzen, wie andere Gegenstände, z.B. meine Schultasche, wiegen könnte.	Gewicht: Anlässe im Alltag, Dinge zu wiegen (Einkauf, Kochen usw.).
					Rauminhalte: Die Lernenden vergleichen beim Umfüllen, Verringern oder Vermehren von Mengen in Gefäße deren Größen. Zum Beispiel wird zum indirekten Vergleich eine Menge Flüssigkeit durch die Nutzung eines zur Verfügung stehenden Bechers genutzt. Für das standardisierte Messen wird dann auf Messgerät, wie z.B. Messbecher, Literflaschen usw. verwiesen. Als Maßeinheit für das Volumen wird zunächst nur das Hohlmaß Liter eingeführt (s.Beziehung zum Kompetenzbereich RuF) Die abgebildeten Zahlen werden als Maßzahlen kennen gelernt und angewendet (s.Beziehung zum Kompetenzbereich ZuO). Stützpunktvorstellungen sind hier: Glasfüllung 200 ml, Eimer 5 l usw. Lernende befassen sich noch nicht mit dem Volumenbegriff als zusammengesetzte Größe. Im Vordergrund stehen Hohlmaße um den Inhalt von Behältern (Fassungsvermögen) mit der Basiseinheit Liter messen zu können.	Ich weiß, dass die Menge von Füssigkeiten mit Hilfe von Messbechern oder Literflaschen bestimmt werden kann und mit den Maßeinheiten Liter (l) und Milliliter (ml) angegeben wird. Ich kann schätzen, wieviel Wasser in ein Gefäß passt, weil ich weiß, dass in meine Trinkflasche genau ein Liter passt. Dieses Wissen hat mir geholfen eine Vorstellung zu entwickeln, wieviel Flüssigkeit man für einen 1 Liter braucht.	Rauminhalte: vielfältige Angebote zum Umfüllen, Verringern, Vermehren von Mengen im Alltag (Flüssigkeiten, Rezeptzutaten usw.). Becherrezepte (Angaben werden in der Anzahl von Bechern gemacht).
					Zeitspannen: Die Lernenden interessieren sich für zeitliche Abläufe: erst – dann, etwas geht schnell oder dauert lange. Wann geschieht etwas? Im Tagesverlauf werden Zeiteinheiten sachbezogen thematisiert (Uhrzeit, Sekunden, Minuten, Stunden). Messgeräte für die Maßeinheiten Stunden, Minuten, Sekunden usw.): Uhren, Stoppuhren, Sanduhren usw. werden genutzt. Zur Orientierung dienen Skalenwerte in Form von Zahlen oder Uhrzeigerstellungen (Beziehung zum Kompetenzbereich ZuO), diese geben auch ohne entfaltetes Anzahlverständnis als Abbildung Orientierungen ((Beziehung zum Kompetenzbereich SufZ). Die Anwendung eine Kalenders beinhaltet die Auseinandersetzung mit den Zeitspannen Tage, Wochen, Monate und Jahre ((Beziehung zum Kompetenzbereich ZuO). Stützpunktvorstellungen: Zeitspanne 15 Min. Hofpause Lernende nutzen standardisierte Zeiteinheiten, um sich im Tagesverlauf zu orientieren. Die Maßeinheiten der Uhrzeit: Sekunden, Minuten, Stunden beziehen sich auf einen 24-Stunden-Tag und werden auf digitalen oder analogen Uhren erkannt und abgelesen und in Beziehung zueinander gebracht (Entfaltetes Anzahlverständnis s. Beziehung zum Kompetenzbereich ZuO). Zunächst werden ganze und halbe Stunden erfasst, dann folgt die Zerlegung der Stunde in 60 Minuten und die Zerlegung der Minute in 60 Sekunden, um Zeitspannen berechnen zu können (Beziehung zum Kompetenzbereich ZuO). Sekunden, Minuten, Stunden, Tag werden in ihren Beziehungen zueinander erkannt. Die Dauer von Abläufen wird geschätzt und überprüft (Beziehung zum Kompetenzbereich DuZ) Kalender: Maßeinheiten Tage, Wochen, Monate, Jahre. Die Gesetzmäßigkeiten bei der Zuordnung der Anzahl von Tagen zur Woche (7 Tage) und zum Monat (28 – 31 Tage) sowie der Wochen zum Monat (4-5 Wochen) und der Monate zum Jahr (12 Monate) werden erkannt, die Beziehungen untereinander erkannt und für die Planung von Aktivitäten im Wochen-, Monats- und Jahresverlauf angewendet (Beziehung zum Kompetenzbereich SfuZ, ZuO). Begriffe wie „vorgestern, gestern, heute, morgen, übermorgen“ werden in Beziehung zueinander gesetzt	Ich kann Zahlen auf der Digitaluhr oder Uhrzeigereinstellungen erkennen und mich auf eine zeitliche Abfolge einstellen. Ich erkenne die Uhrzeigereinstellung als Ganzheit und kann mich daran orientieren. Wenn mir jemand sagt, dass ich noch 15 Min. warten muss, bis wir ins Kino gehen, dann habe ich eine Vorstellung davon, wie lange es noch dauert, weil unsere Hofpause auch immer eine 15 Min lang ist. Ich weiß, dass man eine Stunde in zwei halbe Stunden zerlegen kann. Ich kann eine Stunde in Minuten und eine Minute in Sekunden zerlegen: Eine Stunde hat 60 min. und eine Minute hat 60 sec. Ich weiß wieviel Tage eine Woche, ein Monat, wieviel Monate ein Jahr hat und wie die Monate heißen. Ich kann den Kalender nutzen, um mich über Tage, Wochen, Monate und Jahre zu informieren. Wichtige Ereignisse (Ferien, Geburtstage, Besuche …) sind im Kalender notiert. Ich sehe hier, was in dieser Woche, in diesem Monat, diesem Jahr passieren wird. Ich kann sagen was gestern, vorgerstern und heute passiert ist und bin gespannt, was morgen, übermorgen, in einer Woche usw. alles passieren wird.	Zeitspannen: Tagesabläufe/Abläufe werden strukturiert abgebildet und mit Zeitangaben versehen. Dazu werden auch verschiedene Uhrmodelle (analog und digital) eingeführt und das Ablesen zunächst durch Abbildungen der Zeit eingeübt (Sachunterricht Thema Uhr). Timer und Sanduhren veranschaulichen Zeitrahmen für Unterrichtsphasen. Kalender werden genutzt, um langfristige zeitliche Abläufe und Ereignisse zu veranschaulich. Verlinken: Datei Hehn-Oldiges Kalender fehlt???
					Geld (Werte). Da es sich bei Geldwerten nicht um eine messbare physikalische Größe handelt, werden die Lernenden mit einer gesellschaftlich vereinbarten Zählgroße vertraut gemacht (Franke/Ruwisch 2010, S. 182). Die Lernenden nutzen Geld zum Einkaufen und benötigen Wissen über den Wert von Waren und den Wert der Münzen und Scheine für die Maßeinheiten Cent und Euro. Was kostet etwas? Wie viel Geld steht zur Verfügung, wie viel Geld wird benötigt, um bestimmte Dinge einkaufen zu können? Zunächst werden Münzen und Scheine durch ihre Gestalt, Material, Farbe unterschieden. Münzen und Scheine werden unabhängig von ihrem symbolischen Gehalt (eine 50 Cent-Münze steht für 50 1 ct.-Münzen, 1 Euro enthält 100 Cent usw.) abgezählt. Die sichtbaren Zahlen auf Münzen und Scheinen erhalten ihren Wert durch die Zuordnung zur Maßeinheit Cent oder Euro als Zählgröße. Die Wertbeziehungen werden dadurch verdeutlicht. Wie viele Cent gehören in einen Euro? Was unterscheidet ein 50 Cent-Stück von einem 50 Euro-Schein? Der Umgang mit den Zählgrößen setzt ein Anzahlverständnis im Zahlenraum bis 100 voraus (ZuO). 10€ können in 5€ -Scheine, 2€ oder 1€ Münzen zerlegt werden. 5€ und 10€-Scheine können zum Bündeln genutzt werden. Multiplikation/Division: 50 Cent können durch 50 mal 1Cent oder 5 mal 10 Cent oder 25 mal 2 Cent gelegt oder entsprechend verteilt werden usw. (ZuO)	Ich weiß, dass ich Geld benötige, um etwas einzukaufen. Ich unterscheide die verschiedenen Münzen und die verschiedenen Scheine an ihrem Aussehen. Ich kann die Scheine und Münzen zählen und dann z.B. sagen, wie viele Eineuromünzen oder wieviel Cent ich habe. Den Wert des Geldes erfasse ich schematisch (Ein 5-Euro-Schein ist mehr wert als ein 50ct.-Stück, denn damit kann ich mehr einkaufen). Ich kann die Zahlen auf den Münzen und Scheinen deuten. Ich weiß, dass ein Euro viel mehr wert ist als ein Cent. Für ein 50 Cent-Stück bekomme ich höchstens ein Brötchen beim Bäcker. Für 50 Euro kann ich mir ein ganzes Legozet kaufen.	Geld: Münzen und Scheine werden ohne entfaltetes Anzahlverständnis ihrem Wert entsprechend sortiert angeboten und führen zu einer ersten Orientierung. Unterscheidung von Cent und Euro wird beim Einkauf oder im Rollenspiel thematisiert. PIKAS: Geld
					Prozessbezogene Kompetenzen Lernende entwickeln mathematischer Fähigkeiten im Bereich Größen und Messen im Kontext des Sachrechnens (PRIMAKOM Sachrechnen in der Grundschule). Probleme oder Fragestellungen aus dem Alltag werden mit Hilfe von Messinstrumenten besprochen. Lernende stellen Fragen im Alltag: Was ist größer, schwerer, heiß, kalt usw.? Wann findet etwas statt? Wie viel Geld benötige ich für einen Einkauf? Worauf muss ich beim Zubereiten von Rezepten achten? Wie und womit kann ich etwas messen? Reicht die Flüssigkeit in der Flasche für mehrere Becher usw.? Die passenden Maßeinheiten werden angewendet und Rechenwege modelliert, kommuniziert, dargestellt, erprobt und reflektiert.	Ich kann mich mit Anderen besprechen, wieviel Geld wir für einen Einkauf benötigen. Ich kann mit Anderen besprechen, wie wir beim Kochen und Backen die im Rezept angegebenen Mengen der Zutaten abmessen können. Ich kann erklären und mit Anderen besprechen, warum es so wichtig ist, beim Basteln, Kochen, Backen, Bauen genau auf die Mengenangaben bzw. Längenangaben zu achten und exakt zu messen. Wenn ich mir selber ein Rezept ausgedacht habe, kann ich die richtigen Mengen notieren und meine Vorgehensweise so darstellen, dass Andere nach meiner Vorlage kochen können.	Prozessbezogene Kompetenzen Größen und Messen dient der Erschließung der Lebenswirklichkeit. Lehrkräfte nutzen Fragestellungen aus Alltags- oder Sachsituationen, um mathematische Lösungswege mithilfe von Messinstrumenten zu beantworten. Die Bedeutung von Messungen wird durch vorbildhafte Nutzung dieser Messinstrumente verdeutlicht (Modellieren, Kommunizieren, Argumentieren, Darstellen). Es wird im Alltag kommuniziert, wenn Maßeinheiten und Messgeräte in bedeutungsvollen Zusammenhängen zum Einsatz kommen und was damit gemessen werden kann. Es wird begründet wozu gemessen werden kann oder muss. Die Darstellung von Maßzahlen auf den Messgeräten Uhren oder Geldscheinen/Münzen wird dazu erklärt und besprochen. Beziehungen der Zahlen zueinander werden thematisiert.
					Umwandeln: Verfeinern und Vergröbern der Maßeinheiten Die Besonderheit im Hinblick auf zahliges Handeln (ZuO) besteht zudem darin, dass nur Maßzahlen derselben Maßeinheit miteinander in Beziehung gesetzt werden können. Die Umwandlung von Maßeinheiten setzt arithmetisches Grundwissen voraus. Erst mit der Entwicklung des Anzahlverständnisses können Lernende mit Maßzahlen rechnen (ZuO). Lernende lernen die Erweiterung natürlicher Zahlen zu Dezimalzahlen im Kontext von Größen und Messen. Voraussetzung für die Einführung von Dezimalzahlen und Bruchzahlen ist das dezimale Stellenwertverständnis https://pikas-mi.dzlm.de/inhalte/zahlvorstellungen-tragfähige-vorstellungen-aufbauen-zr-bis-1mio/einstieg/hintergrund-0 Die Lernenden verwenden verschiedene Maßeinheiten und stellen Größenangaben in unterschiedlichen Schreibweisen dar (umwandeln): - Geldwerte: ct, € - Längen: zuerst cm, m, dann mm, km - Zeitspannen: zuerst Minute, Stunde, Tag, Woche, Monat, Jahr, dann Sekunde - Gewichte (Masse): g, kg, t - Volumina: ml, l - Datenmengen: Byte, kB, MB Die Lernenden verstehen die Umrechnungsoperation innerhalb einer Maßeinheit und führen sie durch.	Ich kann Größen in verschiedene Einheiten zerlegen und zusammensetzen, z.B. 1m 50cm = 1,5m.	Sachrechnen beinhaltet fächerübergreifende Bezüge (naturwissenschaftlich, geografisch, gestalterische Techniken, Hauswirtschaft usw.) und findet in Projekten Anwendung. PIKAS Fortbildung Gute Aufgaben https://pikas.dzlm.de/fortbildung/gute-aufgaben/73-sachsituationen Roth, J. https://juergen-roth.de/skripte/did_grundschulmathematik/Did_GS_II_Sachrechnen_1_Typen_von_Sachaufgaben.pdf https://juergen-roth.de/skripte/did_grundschulmathematik/Did_GS_II_Sachrechnen_5_Groessen.pdf Um Größen in verschiedenen Einheiten und Schreibweisen darzustellen, eignet sich eine Stellentafel (Franke & Ruwisch, 2010, S. 199)
					„Rechnen mit Größen“ (Franke/Ruwisch 2010/Ruwisch, S. 184) Die Lernenden rechnen mit Größen, zuerst mit nur ganzzahligen Maßzahlen, dann auch mit Dezimalzahlen. - Die Lernenden setzen Maßeinheiten in Beziehung zueinander und zerlegen und setzen sie dezimal (außer die Größe „Zeit“ zusammen. - Die Lernenden prüfen umgewandelte Größen mit Rückgriff auf Größenvorstellungen auf Plausibilität. - Die Lernenden verrechnen gleiche und unterschiedliche Maßeinheiten miteinander. - Die Lernenden vernetzen Darstellungen beim Rechnen mit Größen kontinuierlich (Handlung, Bild, Sprache, Mathesprache).	Ich kann mit verschiedenen Größen (…) rechnen. / Ich kann mit Größen, die mit der Kommaschreibweise angegeben sind, rechnen. Ich kann prüfen, ob ich die Größe richtig umgerechnet habe, indem ich mir die Maße vorstelle. Ich kann mit gleichen und unetrschiedlichen Maßeineiten rechnen. Ich kann zu Sachsituationen und Bildern die passende Rechnung nennen und erklären und zu vorgegebenen Rechnungen eine Sachsituation finden.	Mit Größen umgehen und rechnen: https://pikas.dzlm.de/unterricht/gr%C3%B6%C3%9Fen-und-messen/gr%C3%B6%C3%9Fenvorstellungen-und-umgang-mit-gr%C3%B6%C3%9Fen/mit-gr%C3%B6%C3%9Fen-umgehen-rechnen
					Bruchzahlen Die Lernenden nutzen im Alltag gebräuchliche Bruchzahlen bei Größenangaben und wandeln diese in andere Einheiten um, z.B. ¼ Stunde = 15 Minuten.	Ich kann Maße mit Brüchen angeben und in andere einheiten umrechnen ( ½, ¼, ¾ )	Um frühzeitig Bruchvorstellungen aufzubauen, sind Kreisdarstellungen bei der Uhr, Längen/Balken, z.B. Meter, und Flächendarstellungen, z.B. m2, geeignet.
					Messen – Die Lernenden verstehen, dass eine Maßzahl ausdrückt, wie oft eine Einheit vorhanden ist, – nutzen das Grundprinzip des Messens bei der Bestimmung von Längen, Zeitspannen, Gewichten, Flächeninhalten, Rauminhalten, – kennen verschiedene Einheiten für Längen, Zeitspannen, Gewichte, Flächeninhalte und Rauminhalte, – haben Stützpunktvorstellungen von verschiedenen Größeneinheiten. – können Größen an Skalen ablesen, – nutzen das Grundprinzip des Messens als Vergleichen mit (Standard-)Einheiten, z. B. bei der Bestimmung von Längen, Flächeninhalten und Volumina, auch in Sachsituationen.	Ich weiß, dass das Ergebnis des Messvorgangs angibt, wie oft eine Einheit vorhanden ist. Ich kann Längen Zeitspannen, Gewichte, Flächeninhalte und Rauminhalte messen. Ich kenne verschiedene Einheiten für Längen, Zeitspannen, Gewichte, Flächeninhalte und Rauminhalte Ich kann Beispiele nennen für Dinge, die so lang und so schwer wie eine Größeneinheit sind. Ich kann Größen an Skalen ablesen. Ich nutze Messergebnisse beim Vergleichen.	Stützpunktvorstellungen werden erweitert und verfeinert: https://pikas.dzlm.de/unterricht/st%C3%BCtzpunktvorstellungen-aufbauen
					Einheiten von Größen wählen und umwandeln Die Lernenden wählen Einheiten von Größen situationsgerecht aus (insbesondere für Zeit, Masse, Geld, Länge, Fläche, Volumen und Winkel), wandeln Größeneinheiten um, können mit unterschiedlichen Größeneinheiten rechnen, indem sie sie zuerst in die gleiche Einheit umwandeln.	Ich wähle eine geeignete Größeneinheit aus, z.B. gebe ich die Länge eines Nagels in mm und die Länge des Reisewegs in km an. Ich kann eine Größenangabe von einer Einheit in eine andere Einheit umwandeln. Ich kann mit Größen rechnen, die verschiedene Einheiten haben. Dafür wandle ich sie zuerst in die gleiche Einheit um.	Stellenwerttafeln zum Umwandeln verwenden, Bezug zum Dezimalsystem herstellen.
					Schätzen Die Lernenden schätzen und bestimmen Längen, Winkel, Umfänge von Vielecken.	Ich kann von vertrauten Dingen die Länge und das Gewicht schätzen. Ich kann Längen schätzen. Ich kann Winkelmaße schätzen. Ich kann Umfänge von rechteckigen, quadratischen, vieleckigen und runden Flächen schätzen.	Damit Lernende schätzen können, brauchen sie Stützpunktvorstellungen und Messerfahrungen: an vorhandene Stützpunktvorstellungen anknüpfen, deren Erweiterung unterstützen, und vielfältige Messerfahrungen ermöglichen.
					Flächeninhalt Die Lernenden schätzen und bestimmen Flächeninhalte von Rechtecken, Kreisen Dreiecken, Parallelogrammen, zusammengesetzten Figuren und Flächen, vergleichen Flächen durch Übereinanderlegen, Auslegen oder Zerlegen, bestimmen den Flächeninhalt in unterschiedlichen Einheiten und können diese umrechnen, bestimmen Flächeninhalte von zusammengesetzten Flächen durch Ergänzen oder Zerlegen, berechnen Seitenlängen aus gegebenen Flächeninhalten mithilfe passender Formeln, formulieren Terme mit Variablen zur Flächenberechnung.	Ich kann die Flächeninhalte von Rechtecken, Dreiecken und Vierecken und Kreisen schätzen und berechnen. Ich kann durch Übereinanderlegen, Auslegen oder Zerlegen entscheiden welche Fläche größer ist. Ich kann den Flächeninhalt eines Rechtecks in Quadratmetern und in Quadratzentimetern bestimmen. Ich kann Flächeninhalte von zusammengesetzten Flächen durch Ergänzen oder Zerlegen bestimmen. Ich kann Seitenlängen aus Formeln für den Flächeninhalt von Dreiecken und Vierecken berechnen, wenn Flächeninhalt gegeben ist. Ich kann für Flächenberechnungen Terme mit Variablen finden.	Maßbezeichnungen m2, dm2, cm2 besprechen: damit Flächeninhalte von Längenmaßen unterschieden werden können, sind andere Bezeichnungen notwendig. Schreibweise und Sprechweise klären: Was bedeutet die hochgestellte 2? Verstehens- und sprachförderliches Unterrichtsmaterial zum Thema „Flächeninhaltsformel für Rechtecke verstehen und begründen“: https://sima.dzlm.de/sites/simams/files/uploads/sima5-005-unterrichtsmaterial-flaecheninhaltsformel-231118.pdf
					Umfang Die Lernenden schätzen und bestimmen Umfänge von Rechtecken, Kreisen Dreiecken, Parallellogrammen, zusammengesetzten Figuren (Vielecke) und Flächen.	Ich kann den Umfang von Flächen schätzen und bestimmen. Ich kann durch Zerlegen und Ergänzen Umfänge und Flächeninhalte von geradlinigen Figuren bestimmen.	Besprechen, wie der Umfang gemessen wird. Wenn mit Variablen gearbeitet wird, evtl. Seiten und Variablen mit gleicher Farbe kennzeichnen.
					Oberfläche Die Lernenden schätzen und bestimmen die Oberfläche von Quadern, Würfeln, einfachen Prismen, Zylindern, Pyramiden, Kegeln und zusammengesetzten Körpern, erläutern die Bestandteile von Formeln für Oberflächen.	Ich kann Oberflächeninhalte von Körpern bestimmen. Ich kann den Inhalt der Oberfläche eines Quaders berechnen. Ich kann Oberflächeninhalte von geraden, spitzen, runden und zusammengesetzten Körpern (Pyramide, Kegel, Kugel) bestimmen. Ich kann erklären, was die einzelnen Teile einer Formel zur Oberflächenberechnung bedeuten.	Um die Oberfäche von Köepern (Ausnahme Kugel) zu bestimmen, ist bei bei ebenmäßigen Körpern die gedankliche oder tatsächliche Konstruktion eines Körpernetzes notwendig. Bei Zylindern, Kegeln oder Kegelstümpfen muss die gedankliche oder tatsächliche Abwicklung des Körpers erfolgen. So entstehen jeweils ebene Figuren, deren einzelnen Flächen bestimmt werden können. Voraussetzung dafür ist, dass die Formeln für Fächenbestimmung abrufbar sind. Evtentuell sind Wiederholungen notwendig. https://didaktik.mathematik.hu-berlin.de/user/filler/geometriedidaktik/09_Koerpergeometrie.pdf
					Volumen Die Lernenden schätzen und bestimmen das Volumen von Quadern, Würfeln, einfachen Prismen, Zylindern, Pyramiden, Kegeln, Kugeln und zusammengesetzten Körpern. Die Lernenden bestimmen das Volumen in unterschiedlichen Einheiten und können diese umrechnen, erläutern die Bestandteile von Formeln für Volumina. Die Lernenden erklären Zusammenhänge von Körpern und Volumen.	Ich kann das Volumen von Körpern bestimmen. Ich kann das Volumen eines Prismas bestimmen und auch mein Vorgehen erläutern. Ich kann das Volumen von zusammengesetzten Körpern bestimmen. Ich kenne verschiedene Volumeneinheiten und kann sie ineinander umrechnen. Ich kann erklären, was die einzelnen Teile einer Formel zur Oberflächenberechnung bedeuten. Ich kann Seitenlängen aus der Volumenformeln von Körpern berechnen, wenn das Volumen gegeben ist. Ich kann erklären, wie das Volumen von Zylindern und Kegel sowie quadratischer Pyramide und Quadern zusammenhängt.	Volumen Quader: Vorstellen, dass der Quader aus kleinen Würfeln gebaut ist. Aber: Rauminhalte müssen nicht die Form eines Quaders oder Würfels haben, sondern können beliebige Formen haben. Maßbezeichnungen m3, dm3, cm3 besprechen: damit Rauminhalte von Flächeninhalten und Längenmaßen unterschieden werden können, sind andere Bezeichnungen notwendig. Schreibweise und Sprechweise klären: Was bedeutet die hochgestellte 3? Partnerarbeit: Jemand baut einen Körper aus Holzwürfeln, jemand anderes versucht durch Berechnen und Überlegen, wie viele Würfel gebraucht wurden.
					Berechnungen am Kreis Die Lernenden bestimmen Größen von Kreisen und Figuren die Kreise enthalten: Umfang, Radius, Flächeninhalt, rechnen Größen von Kreisen ineinander um. bestimmen das Volumen und die Oberfläche von Zylindern und Kegeln. bestimme Größen von Kreissektoren: Bogenlänge, Winkel und Flächeninhalt.	Ich kann den Umfang von Kreisen und von Figuren, die Teile von Kreisen enthalten, bestimmen. Ich kann zwischen Radius, Umfang und Flächeninhalten von Kreisen hin- und her rechnen. Ich kann das Volumen und die Oberfläche von Zylindern und Kegeln bestimmen. Ich kann Bogenlängen, Winkel und Flächeninhalte von Kreissektoren bestimmen.	Für die Berechnungen ist ein Taschenrechner notwendig. Falls mit gerundeten Zahlen gerechnet wird, besprechen, auf wieviele Nachkommastellen gerundet werden soll.
					Die Lernenden nehmen in ihrer Umwelt gezielt Messungen vor, auch mit Hilfe digitaler Medien (als Informationsquelle oder Messinstrument) entnehmen Maßangaben aus Quellenmaterial, führen damit Berechnungen durch und dokumentieren die Ergebnisse sowie den gewählten Weg in Bezug auf die Sachsituation.	Ich kann Alltagsprobleme lösen, die mit dem Messen und Berechnen von Mengen und Größen zu tun haben.	Zunächst Sachaufgaben zu bekannten Sachsituationen, mit leicht verständlichem Text und zu Größen, zu denen die Lernenden über Stützpunktvorstellungen verfügen, bearbeiten. Später Fermi-Aufgaben bearbeiten und Aufgaben zu Zeitungsartikeln, aus denen die Lernenden die relevanten Größen entnehmen und Fragestellungen entwickeln. Digitale Medien: Google Maps für Entfernungen, Internet zum Finden von Informationen, z.B. zum Gewicht von bestimmten Gegenständen, Nutzung eigener gesammelter Daten, z.B. von Fitnessarmbändern. Evtl. Einüben von Teilschritten bei der Bearbeitung von Sachaufgaben: https://sima.dzlm.de/sites/simams/files/uploads/sima5_textaufgaben-did-kommentar_190313.pdf

Zum Inhaltsverzeichnis zurück

Tabelle 3.3: Raum und Form

Abkürzungen Tabellen: b = basal | e = elementar | p = primär | s = sekundär


					Teilbereich: Raum und Form (RuF)
					Muster, Strukturen und funktionale Zusammenhänge im Teilbereich Raum und Form (MSufZ) Lernende begegnen Strukturen in regelmäßigen geometrischen Mustern, die sie erkennen, beschreiben und in mathematischen Kontexten nutzen lernen. Die Strukturen im Hinblick auf die Eigenschaften geometrischer Objekte (Körper, ebene Figuren) und Raumvorstellungen (z.B. Pläne) und deren Beziehungen untereinander werden erkannt und angewendet (KMK 2o22, S. 17).			Pädagogische Angebote Lehrkräfte thematisieren die Gesetzmäßigkeiten und Muster beim Beobachten und Erstellen von Abbildungen, und bieten Anlässe, diese zu erkunden, zu beschreiben und darzustellen.
b	e	p	s	ILZ	Stufe in Erwachsenensprache	Stufe in Kindersprache	Lernbausteine
				1a	Sinnliche Welterkundung Allgemein-mathematische Kompetenzen basieren auf einer aktiv-entdeckenden Auseinandersetzung durch Zufallshandlungen mit Dingen/Gegenständen Inhaltsbezogene mathematische Vorerfahrungen Die Lernenden handeln zufällig in ihrem Körper- und Nahfeld. Durch die Komplexität der Situation können sie basale Erfahrungen in den sich überschneidenden Kompetenzbereichen machen. Die Gestaltung des Nah- und Greiffelds ermöglicht ihnen das Lernen durch Berühren, Bewegen, Beobachten interessanter Eigenschaften und Merkmale: Raumerfahrungen durch Lagerungsorte (Rollstuhl, Little Room usw.), Raumbegrenzungen, räumliche Anordnung von Dingen (oben- unten, vorne – hinten, innen – außen) sind bedeutsam für den Kompetenzbereich Raum und Form (RuF), basale Vorerfahrungen durch regelmäßige und wiederholte zeitliche Abläufe und räumliche Angebote in den Kompetenzbereichen Muster und Strukturen/ Strukturen und funktionaler Zusammenhang (MSfuZ) sowie Daten, Häufigkeit und Wahrscheinlichkeit/Daten und Zufall (DuZ), sinnliche Erfahrungen durch die Beschaffenheit von Dingen (einschließlich Geruch und Geschmack) mit weiteren unterschiedlichen Eigenschaften und Merkmalen (hart – weich, farbig, glatt, laut – leise, hell – dunkel usw.) Formen (rund – eckig) sind bedeutsam für den Kompetenzbereich Raum und Form (RuF), Erfahrungen bei den Zufallshandlungen mit Gewicht, Größe, Entfernung (groß – klein, leicht – schwer, nah – weit) sind bedeutsam für den Kompetenzbereich Größen und Messen (GuM) Die benannten Erfahrungen ermöglichen die Entwicklung der Fähigkeit, Dinge grundsätzlich zu unterscheiden. Das ist wiederum eine Voraussetzung für das Bilden von Mengen (Sortieren) im Kompetenzbereich Zahl und Operation (ZuO)	Ich kann, was um mich geschieht hören, sehen, spüren, riechen, schmecken, fühlen. Ich kann die Dinge, die ich zufällig ergreife, berühren, belecken und in Bewegung bringen. Dabei erfahre ich, dass sich Gegenstände und Materialien unterschiedlich anfühlen. Ich beginne, ganz bestimmte Personen, Gegenstände und Materialien, Muster, Formen zu bevorzugen und kann dies durch Zuwendung, Wiederholung, durch Mimik, Gestik und durch Laute zum Ausdruck bringen.	Gestaltung des Nah- und Greiffelds: Materialien und Gegenstände sind im Nah- und Greiffeld angebracht, die leicht berührt und bewegt werden können die Geräusche oder Lichteffekte auslösen die kontrastreiche Muster und Farben haben die aus unterschiedlichen Formen und Materialen bestehen Handlungen werden von Bezugspersonen und anderen Lernenden beobachtet und im Dialog gespiegelt. Materialien, die zu aktiven Wiederholungen anregen, werden gezielt angeboten und durch weitere, mit ähnlichen Eigenschaften ergänzt.
				1b	Welterkundung durch unspezifisches Operieren Aktive Wiederholungen erweitern die allgemein-mathematische Kompetenzen durch die aktiv-entdeckenden Auseinandersetzung mit Dingen/Gegenständen Inhaltsbezogene mathematische Vorerfahrungen Interessante Effekte durch Dinge und Materialien im Körper-, Nah- und Greiffeld werden von den Lernenden aktiv wiederholt und die inhaltsbezogenen Vorerfahrungen zu den Kompetenzbereichen (MSfuZ, RuF, GuM, ZuO, DuZ s.o.) können sich jeweils festigen und erweitern. Dinge/Gegenstände werden mit dem Mund, den Händen oder Füßen erkundet (Berühren, Klopfen, Werfen usw.). Erreichbare Materialien und Dinge ermöglichen so die aktive Wahrnehmung und zunehmende Unterscheidung von Gegenständen und deren Eigenschaften: Länge, Gewicht, Größe, Beschaffenheit, Form, Farbe, Klangeffekte, Geruch, Geschmack usw.	Ich kann Bewegungen, die es mir ermöglichen, für mich bedeutsame Dinge zu erreichen oder Effekte herbeizuführen, aktiv wiederholen. Ich kann diese Dinge mit dem Mund, den Händen und den Füßen durch Berühren, Klopfen, Werfen usw. immer genauer erkunden und so Größe, Beschaffenheit, Form, Farbe, Klangeffekte, Geruch, Geschmack usw. wahrnehmen. Ich erfahre durch aktive Wiederholungen, dass sich die Gegenstände und Dinge in meiner Umgebung unterschiedlich anfühlen, dass sie unterschiedlich aussehen, riechen, schmecken oder klingen.	Gestaltung des Nah- und Greiffelds: Bevorzugte Gegenstände, Materialien werden so angebracht, dass sie erreichbar sind aktive Wiederholungen ermöglichen und Zeit für die selbsttätige Erkundung zur Verfügung steht. z.B. Lagerung in Rückenlage auf einem Resonanzbrett, auf dem Materialien getastet werden können. Das Resonanzbrett verstärkt akustische Effekte und animiert zur Erkundung Im Stehständer werden Materialien im Greiffeld angebracht, die durch die aktiven Wiederholungen Spür-, Seh- und Höreindrücke auslösen und die Aufmerksamkeit anregen.
				1c	Welterkundung durch spezifisches Hantieren Spezifisches Hantieren erweitert die allgemein-mathematischen Kompetenzen durch die gezieltere aktiv-entdeckende Auseinandersetzung mit Dingen/Gegenständen und deren Funktion Inhaltsbezogene mathematische Vorerfahrungen Die Lernenden erkunden gezielt Dinge/Gegenstände und Materialien in ihrer unmittelbaren Umgebung und wenden als bewährt erfahrene Handlungsschemata (Lecken, Beißen, Klopfen, Werfen, Fallenlassen usw.) an. Auf diese Weise erfahren sie deren unterschiedlichen Eigenschaften (GuM, ZuO), deren räumliche Anordnungen (RuF) und die Veränderbarkeit von Mengen (Teile-Ganzes-Schema) (ZuO) Die funktionsbezogene Nutzung ist noch nicht erschlossen. Als bewährt erfahrene Handlungsschemata werden auf Neues angewendet (Lecken, Beißen, Klopfen, Werfen, Fallenlassen usw.). Die Unterschiede in den Dingen/Gegenständen und Materialien führen zu neuen Erfahrungen. Allgemeine mathematische Vorerfahrungen (Kommunizieren) Durch die Beobachtung anderer Menschen und im Dialog werden die Handlungen verbal gespiegelt und die funktionsbezogene Nutzung von Gegenständen angebahnt.	Ich kann Materialien und Gegenstände mit dem Mund, den Augen und den Händen gezielter erkunden. Ich kann die dabei erprobten Handlungen (Lecken, Beißen, Fallenlassen…) zur Erkundung noch unbekannter Gegenstände anwenden. Ich kann beobachten, wie andere Menschen mit den Gegenständen umgehen und beginne dadurch wahrzunehmen, wie diese genutzt werden. Ich lerne, dass nicht alle meine erprobten Handlungsweisen für jeden Gegenstand geeignet sind. Ich beginne, Gegenstände durch bestimmte Merkmale als zueinander zugehörig wahrzunehmen.	Gestaltung des Handlungsfelds: Der Arbeitsbereich ist so zu gestalten, dass mit den darin erreichbaren Gegenständen hantiert werden kann (abgegrenzter räumlicher Bereich, Multifunktionstisch MFA-Tisch, Tastbretter, Materialkisten). Für das zunächst noch nicht an den Funktionen orientierte Erkunden durch Lecken, Beißen, Klopfen, Werfen usw. müssen Gegenstände und Materialien robust und stabil sein Dadurch wird und ermöglicht, dass die unterschiedlichen Eigenschaften untersucht werden können. Materialkisten (GuM, ZuO) und verschiedene Behältnisse (RuF) werden zeitlich und räumlich verlässlich zur Verfügung gestellt (DuZ, RuF, MSfuZ) . Sie können ausgeleert und eingeräumt werden können. Mengen können umgefüllt, verändert und sortiert werden (MFA-Tisch n. Nielsen) (ZuO, MSufZ, RuF). Tastbretter mit daran befestigtem Material ermöglichen eine intensive Beschäftigung mit deren Eigenschaften (RuF, GuM, MSufZ). Kommunizieren Andere Menschen spiegeln diese Handlungen und zeigen vorbildhaft die funktionsbezogene Nutzung von Gegenständen. Die Nachahmungsfähigkeit wird dadurch angeregt. Inhalts- und prozessbezogene Kompetenzen Bezugspersonen thematisieren zahliges Handeln in Alltagszusammenhängen. Dabei werden die verschiedenen Bedeutungszusammenhänge bei der Verwendung von Zahlwörtern und Ziffern erklärt (Zahlen zum Abzählen, Zahlen zum Messen, Zahlen zum Bezeichnen (Haus-Nr., Auto-Nr.). Beispiele unter PIKAS Mathe ein Kinderspiel Literatur: (Koch u.a.2020) Die Lehrkraft beschreibt konkrete Handlungen im Alltag (bedeutsam für: GuM, DuZ, MSufZ) mit Mathematiksprache und regt zum Entdecken von mathematischen Handlungen an. Sie verwendet vorbildhaft Begriffe aus der Mathematiksprache (Darstellen, Kommunizieren): Zahlen, viel – wenig, mehr – wenige, um eins mehr, sind zusammen usw. Beispiele in: PIKAS: Fachwortschatz Mathematik
					Übergang zum elementaren Zugang: Vorzahlige Handlungen werden mit zahligem Handeln verbunden. Zahlwörter im Alltag (zwei Äpfel, drei Brötchen), in Fingerspielen, Liedern und Geschichten und Ziffern als Abbildungen sowie Mengenwissen (viel – wenig) gewinnen im Alltag an Bedeutung (ZuO). Eigenschaften von Dingen werden verglichen (groß – klein, schwer – leicht, lang-kurz, kalt-heiß) (GuM), räumliche und strukturierte Anordnungen (MSufZ) dienen der Orientierung (oben-unten, hinten-vorne, aufgereiht, nebeneinander), die Gestalt der Dinge wird im Handeln erfahren (rund – eckig) (RuF). Auf zeitliche Abläufe (Tage, Stunden, Minuten) wird verwiesen (erst – dann, gleich – später), Strukturen wiederholen sich (GuM, DuZ, MSufZ).	Ich beginne, Zahlwörter und Zahlen im Alltag wahrzunehmen. Ich interessiere mich für Zahlen und Ziffern im Alltag, in Liedern und Geschichten. Ich handele mit Gegenständen in meiner Umgebung und beginne sie zu vergleichen und zu unterscheiden, ob sie groß oder klein, kurz oder lang, schwer oder leicht sind. Wenn ich mir eine Ansammlung von Gegenständen anschaue, kann ich einschätzen, ob es viel oder wenig Gegenstände sind. Ich kann sagen, wo sich die Dinge befinden (vorne, hinten…) und wie sie angeordnet sind (nebeneinander, übereinander usw.). Ich weiß, dass bestimmte Ereignisse jeden Tag, jede Woche zur gleichen Zeit stattfinden und kann darüber berichten. Ich habe eine Vorstellung dazu entwickelt, was es bedeutet, wenn ich einen Tag oder wenige Minuten auf etwas warten soll.
					Die Lernenden erfahren sich an unterschiedlichen Orten in räumlichen Beziehungen zu Menschen und Gegenständen (hinter, vor oder neben anderen, unter dem Tisch, auf dem Teppich usw.). Sie können sich im Raum orientieren und kennen Wege. Die Lernenden nutzen räumliche Beziehungen in Spiel- und Alltagshandlungen (z.B. Bauen mit Bausteinen, Alltagsgegenstände an ihren Platz stellen). Dabei wird abgezählt ( Beziehung zum Kompetenzbereich ZuO).	Ich weiß, wer oder was vor mir/ hinter mir/neben mir steht und kann das ansagen. Ich kann selbst an andere Stelle gehen und Dinge an gut erreichbare Orte stellen. Ich weiß, wo ich mich gerade befinde und wo für mich bedeutsame Objekte sind Ich kann mich selbstständig im Raum, im Haus und in unmittelbarer Umgebung bewegen, weil ich mir die Wege (zur Toilette, zur Küche, auf den Spielplatz) bereits gemerkt habe. Ich unterscheide Dinge, die rollen (Röhren, Kugeln, Bälle) von Dingen, die nicht rollen (Bausteine, Würfel) Ich unterscheide Dinge, die rund sind (Kugeln, Murmeln, Bälle) oder eckig sind (Kästen, Würfel, Bausteine). Ich kann Dinge nach unterschiedlichen Farben sortieren.	Räumliche Anordnungen von Dingen/Gegenständen und Personen werden sprachlich begleitet und beim Aufreihen, Nebeneinanderstellen oder Wegräumen benannt (hinter, vor, neben, auf, unter usw.). Bauecken mit Bausteinen, Lego usw. laden zum Experimentieren (Stapeln, Bauen usw.) ein, Bauwerke werden fotografiert, zeichnerisch abgebildet und nachgebaut usw. Hüpfkästchenspiele ermöglichen die räumliche Nutzung von geometrischen Grundformen und Raumorientierung. Brettspiele ermöglichen die Unterscheidung geometrischer Grundformen, bieten Muster und räumliche Orientierung an (MSfuZ ZuO).
					Die Lernenden interessieren sich für Dinge, Materialien und Gegenstände, die sich zum Umfüllen, Ausleeren, Einräumen usw. eignen (innen – außen). Beim Bauen mit Bausteinen, Stapeln, Aufeinandersetzen, Ineinanderstecken usw. werden Erfahrungen mit oben- unten, innen – außen gemacht. Dinge/Gegenstände können rund sein und wegrollen (Bälle, Röhren usw.) oder sind eckig. Dinge können einfarbig, farbig, gemustert gestaltet sein. Behältnisse können gefüllt oder geleert werden. Es passt viel hinein oder wenig (Mengen (Beziehung zum Kompetenzbereich ZuO), Gewicht (Beziehung zum Kompetenzbereich GuM)). Sie können rund (Dosen, Eimer) oder eckig (Brotdosen usw.) sein. Es gibt evtl. passende Deckel, die die entsprechende Form haben. Es kann verglichen werden, wovon es mehr oder weniger gibt (Stück-zu-Stück-Zuordnung) (Beziehung zum Kompetenzbereich ZuO). Die Lernenden machen erste Erfahrungen mit geometrischen Grundformen, die zu Körpern gehören (Tischset mit großem Kreis für den Teller und kleinem Kreis für Tasse oder Glas usw.). Puzzle-Umrisse werden erkannt und Puzzle-Teile eingefügt. Muster werde nachgelegt (Beziehung zum Kompetenzbereich MSufZ). Geometrische Grundformen im Alltag (Verkehrszeichen, Verpackungen usw. werden entdeckt und verglichen. Lernende vergleichen beim Stempeln und Basteln, Abbildungen, Formen und Farben. Es werden Muster angefertigt oder fortgesetzt (Beziehung zum Kompetenzbereich MSfuZ). Beim Ausschneiden werden Umrisse beachtet. Beim Papierfalten wird Symmetrie einbezogen. In der zeichnerischen Entwicklung werden Abbildungen verfeinert. Muster werden erfunden. Bei Brettspielen werden flächige Anordnungen und Muster zur Orientierung genutzt (Beziehung zu den Kompetenzbereichen MSfuZ, ZuO).	Ich kann Bausteine aufeinander oder nebeneinander anordnen und so herausbekommen, wie ein stabiles Bauwerk entsteht. Ich kann für die verschiedenen Dosen und Kisten die richtigen Abdeckungen finden und sie verschließen, öffnen, füllen und wieder verschließen. Ich kann beim Tischdecken passenden Unterlagen auswählen und alles hübsch anordnen. Ich kann Puzzleteile zusammenfügen, indem ich mir die Formen genau anschaue und dann nach dem passenden Puzzleteil suche. Ich prüfe, ob und wie das ausgewählte Puzzleteil hineinpasst. Ich kann vorgegebene Muster und Reihen (z.B. Folge von farbigen Perlen) fortsetzten. Ich kann schöne Muster erfinden und damit Abbildungen verschönern. Ich kann an einer vorgebenen Linie entlang ausschneiden. Ich kann Papier so falten, dass zwei gleichaussehende Hälften entstehen.	Behältnisse aus dem Alltag werden betrachtet, verglichen, sortiert. Sie werden gefüllt, umgefüllt oder geleert. Sand- und Wasserspiele ermöglichen Erfahrungen mit Behältnissen und Gewichten (GuM). Formen können verändert werden: Serviette oder Toastbrot: vom Viereck zum Dreieck durch Falten und Schneiden. Falten mit Papier, Geschenke verpacken. Die Umrisse von Körpern (aufgestellte Röhre, rechteckige und quadratische Bausteine, Dosen werden gezeichnet. Die Körper können dann den gezeichneten Flächen wieder zugeordnet werden. Konkrete Beispiele in: Stiftung Haus der kleinen Forscher (Hrsg.) (2014): Mathematik in Raum und Form entdecken PIKAS Mathe ein Kinderspiel
					Prozessbezogene Kompetenzen Die Lernenden erfahren Sachprobleme in räumlichen Beziehungen, im Hinblick auf Abbildungen usw., die besprochen werden. Worauf muss geachtet werden? Wie können wir Lösungen finden? Die eigenen Handlungen (beim Bauen, Basteln, Zeichnen) werden beschrieben und verglichen.	Ich kann gemeinsam mit den anderen darüber nachdenken, wie wir unseren Raum noch besser gestalten können, damit die Wege frei sind und alles für Jeden gut erreichbar ist. Ich kann Anderen erklären, wie ich beim Bauen, Basteln und Zeichnen vorgegangen bin und wir können unsere Vorgehensweisen miteinander vergleichen.	Prozessbezogene Kompetenzen Lehrkräfte regen zum Austausch über Erfahrungen an (Problemlösen, Vergleichen, Kommunizieren). Gesetzmäßigkeiten werden reflektiert (Beziehung zum Kompetenzbereich MSfuZ). Der Wortspeicher PRIMAKOM Raum und Form wird nach und nach eingeführt.
					Entwicklung des räumlichen Vorstellungsvermögens: Weiterentwicklung der Fähigkeit räumliche Beziehungen zu erkennen, zu beschreiben und nutzen. Weiterentwicklung des Orientierungsvermögens im Raum (Wege, Pläne, Ansichten) Die Lernenden bewegen sich im Raum, verändern ihre Lage in Beziehungen zu anderen Menschen, zum Raum oder zu Objekten. Sie nehmen die Lagebeziehungen von Gegenständen/Objekten wahr und verändern sie. Im Tun werden immer ausdifferenziertere Begriffe (vor, hinter, links, rechts, neben, unter, über usw.) zu Lagebeziehungen und Ortsbeschreibungen (oben rechts, unten links usw.) erworben. Die Fähigkeit, Größe, Position, Entfernung von Objekten in Bezug zu sich selbst, dem Raum und zu anderen Objekten einzuschätzen wird so erworben. Die Lernenden nutzen Wege in Alltagszusammenhängen und lernen, diese durch Richtungsbegriffe zu beschreiben (geradeaus, bis zur nächsten Ecke, nach links, die Treppe hinunter usw.) (Längenmaße s. GuM.) Die Übertragung konkreter Wege auf Abbildungen (Pläne) führt zu einer räumlichen Vorstellung und zur Abstraktion. Lernende können Wege durch Linien abbilden und Wege durch Labyrinthe finden und zeichnen. Prozessbezogene Kompetenzen Lernende tauschen sich über Wege aus, beschreiben diese und können Beschreibungen umsetzen.	Ich kann mich oder Dinge an unterschiedlichen Orten platzieren. Ich verstehe und kann sagen, ob sich etwas oben, unten, hinten oder vorne usw. befindet, ob es weit oder nah von mir entfernt ist usw. Ich kann mir einfache Pläne, Ansichten zu mir bekannten Umgebungen (meine Einrichtung, meine Wohnumgebung) genau anschauen und dann deuten. Deshalb kann ich auch erklären, was auf den Plänen oder Ansichten zu sehen ist. Ich kann auf einer Abbildung zu einem mir bekanntem Ort markieren, wo sich bestimmte Dinge befinden.Ich kann Anderen genau beschreiben, wie sie einen Ort in meiner Umgebung erreichen können. Ich höre genau zu, wenn mir Andere einen Weg beschreiben und folge der Beschreibung.	Räumliches Vorstellungsvermögen wird gefördert, iindem Alltagsgegenstände im Raum angeordnet werden (ins Regal, neben die Bücher, auf den Tisch usw.).Lernende werden angeregt, sich selbst im Raum und in Lagebeziehungen zu Gegenständen zu verorten. indem Wege geplant und abgelaufen werden (im Gebäude, im Viertel usw.). Pläne, auf denen die konkreten Wege abgebildet sind, werden dazu eingeführt und verwendet und führen über die Veranschaulichung zur Abstraktionsfähigkeit. Beispiele PRIMAKOM Raumorientierung PRIMAKOM Vom Raum in die Ebene Prozessbezogene Kompetenzen Wortspeicher: Raum- und Richtungsbegriffe werden systematisch im Kontext von Alltagshandlungen verwendet und gesichert (Roth 2012). Im Austausch mit andern wird über den Umgang mit Gegenständen und Plänen kommuniziert, dargestellt und argumentiert.
					Die Lernenden erkennen, beschreiben und nutzen räumliche Beziehungen, indem sie zwei- und dreidimensionale Darstellungen zueinander in Beziehung setzen Würfelnetze (Bereich Raumorientierung und Raumvorstellung) Die Lernenden können Würfelnetze erkennen und auf ihre Vollständigkeit überprüfen. Die Lernenden können Würfelnetze erstellen. Die Lernenden können weitere Körpernetze erstellen, z.B. Quader, Tetraeder. Die Lernenden können Körpernetze vergleichen. Die Lernenden können Beziehungen zwischen Würfelnetzen (zweidimensional) und Würfeln (dreidimensional) herstellen und beschreiben	Ich weiß, dass man Körper, gedanklich aufklappen kann und die entstehenden Flächen zusammenhängend aufzeichnen kann. Diese Zeichnungen nennt man Körpernetze. Wenn es sich um einen Würfel handelte, entsteht bei der Zeichnung ein Würfelnetz. Ich kann Würfelnetze erkennen und erstellen. Ich kann auch andere Körpernetze (vom Quader und Tetraeder) erkennen und zeichnen. Ich kann Körpernetze vergleichen und sie den entsprechenden Körpern zuordnen.	Würfelnetze: App Klipp Klapp: https://dlgs.uni-potsdam.de/apps/klipp-klapp Würfel aus Polydronquadraten bauen und eigene Würfelnetze herstellen und die verschiedenen gefundenen Netze abzeichnen.
					Bauplan und Bauwerk Die Lernenden bauen aus Bausteinen oder Würfeln Gebäude, die (nach bildhafter Vorlage unter Berücksichtigung der Lage der Körper zueinander) zerlegt, zusammengefügt und untersucht werden. Sie erkunden die Raum-Lage-Beziehung. Die Lernenden können Bauwerke (Würfelgebäude o.ä.) nach Vorlage bauen. Die Lernenden können zu Bauwerken passende Baupläne (Grundriss o.ä.) erstellen. Die Lernenden können Lagebeziehungen (vor, hinter, unter, über, zwischen, links, rechts o.ä.) nutzen, um Würfelgebäude zu beschreiben. Die Lernenden bauen Gebäude aus ihrer eigenen Vorstellung.	Ich kann Gebäude aus Bausteinen oder Würfeln zerlegen und wieder zusammenfügen. Dazu nutze ich Vorlagen (Abbildungen). Ich sehe, was oben, unten, links oder rechts angeordnet wird und baue das nach. Ich kann mir eine Vorlage zum Bau eines Gebäudes aus unterschiedlichen Bausteinen genau anschauen und entsprechend der Vorlage das Gebäude aufbauen. Dabei prüfe ich laufend, ob mein Bau der Vorlage entspricht oder nicht. Ich kann auch versuchen, etwas nach meiner eigenen Vorstellung zu bauen.	Baupläne werden angeboten, die aus der zweidimensionalen Abbildung in dreidimensionale Anordnung umgesetzt werden. Würfelbauwerke – Klötzchen-App: https://pikas-digi.dzlm.de/sites/pikasdg/files/uploads/Unterricht/Kloetzchen/um_kloetzchen.pdf
					Kopfgeometrie Die Lernenden verändern die Lage von ebenen Figuren und Körpern in der Vorstellung und benennen das Ergebnis der Bewegung (u.a. Kippbewegungen eines Würfels). Entwicklung Aufgabenstellung und Ergebnisdarstellung mit Hilfsmitteln Verwendung von Hilfsmitteln, wenn Aufgabenstellung oder Ergebnisdarstellung ohne Material nicht möglich sind Reine Kopfgeometrie ohne Hilfsmittel	Ich kann in meiner Vorstellung einzelne Würfel eines Bauwerks versetzen und mir vorstellen, wie es danach aussieht. Ich kann mein Ergebnis mit Hilfsmitteln prüfen. Ich kann mir vorstellen, wie ein Körper oder Bauwerk von verschiedenen Seiten aussieht.	Klötzchen-App: https://www.uni-potsdam.de/de/mathematikdidaktik/forschung-projekte/kloetzchen-app App Klipp Klapp: https://dlgs.uni-potsdam.de/apps/klipp-klapp Aufgaben zur Kopfgeometrie in den Känguru-Wettbewerben: https://www.mathe-kaenguru.de/
					Symmetrie Symmetrie kommt in der Natur und in der Umwelt vor. Sie ist Bestandteil von dekorativen oder technischen Mustern (Kunst, Architektur usw.), entsteht beim Basteln, Falten usw. (Beziehung zum Kompetenzbereich MSufZ). Lernende können durch die Auseinandersetzung mit Symmetrie das Verständnis des räumlichen Vorstellungsvermögens, das Erkennen von gegliederten Gestalten und Mustern sowie Erkenntnisse zur Funktionalität von symmetrischen Gegenständen entwickeln. Arithmetisches Wissen (Verdoppeln/Halbieren) wird unterstützt (Beziehung zum Kompetenzbereich ZuO). Symmetrieeigenschaften werden zunächst in Bezug auf die Achsensymmetrie erkundet. Symmetrische Muster können selbst entwickelt und fortgesetzt werden (Beziehung zum Kompetenzbereich MSufZ).	Ich weiß, wie Würfel, Quader, Kugel und Zylinder aussehen und kann Gemeinsamkeiten und Unterschiede erkennen. Ich weiß, dass eckige Gegenstände gekippt und runde Gegenstände gerollt werden können. Ich kann beim Platzieren von Gegenständen beachten, wie und wo ich sie anordne. Ich untersuche wie unterschiedlich groß die Körper sind und vergleiche sie miteinander. Ich kann aus Papier durch Schneiden und Falten Tüten, Schachteln usw. herstellen.	Umgang mit Körpern Lehrkräfte bieten in Alltags- und Sachsituationen die Möglichkeit, Gegenstände mit unterschiedlichen Körpern (Würfel, Quader, Zylinder, Kugel usw.)zu erkunden, ihre Eigenschaften zu berücksichtigen, sie räumlich anzuordnen, die Positionen zu verändern. Beispiele Primakom Inhalt Raum und Form
					Die Lernenden setzen sich durch Schneiden, Falten mit den Eigenschaften von Objekten auseinander (Briefumschläge, Tüten, Schachteln usw.). Prozessbezogene Kompetenzen Die Lernenden vergleichen Körper und erkennen Gemeinsamkeiten und Unterschiede (Würfel, Quader, Kugel, Zylinder). Dazu verwenden sie die Fachbegriffe für die Körper sowie deren Eigenschaften (rund, eckig, kippen, rollen, Länge der Seiten, Anzahl der Ecken usw.). Umfang, Flächen- und Rauminhalt werden untersucht und verglichen. Die Lernenden tauschen sich über ihre Vorgehensweise aus (kommunizieren, darstellen).	Ich habe Fachbegriffe gelernt und eingeprägt, mit denen ich die unterschiedlichen Körper benennen, beschreiben, vergleichen kann und kann mich mit Anderen darüber austauschen. Ich kann Flächeninhalte vergleichen, indem ich Figuren aufeinander lege, indem ich Figuren in Teilstücke zerlege oder indem ich die Flächen mit Einheitsquadraten auslege. Ich kann Rauminhalte vergleichen, indem ich sie mit Einheitswürfeln ausfülle oder mir vorstelle, wie viele Einheitswürfel hineinpassen.	Prozessbezogene Kompetenzen Lernende werden dazu angeregt, zu bauen und sich über ihre Bauweise, Ergebnisse und Eigenschaften der Körper auszutauschen (Darstellen, Argumentieren). Beispiel Primakom Darstellungswechsel
					Geometrisches Abbilden - Ebene Figuren Lernende bilden geometrische Körper mit ihrer Grundform ab (z.B. Stempeln von geschlossenen Zylindern, Würfeln usw.) Grundformen werden abgebildet und nachgezeichnet. Ebene geometrische Figuren werden in der Umwelt gefunden und untersucht. Dazu ist es notwendig, Linien ziehen zu können und Mittel wie Lineal und Geo-Dreieck zu nutzen. Längen werden verglichen (Beziehung zum Kompetenzbereich GuM). Zum Vergleich wird die Anzahl der Ecken, die Länge der Seiten zugrunde gelegt Ebene Figuren und Grundformen können zu Mustern oder Figuren (Tangram) gelegt werden (Beziehung zum Kompetenzbereich MSufZ). Fächerübergreifend Kunst Geometrische Abbildungen werden gedreht, gespiegelt, verschoben. Lernende verknüpfen mit zunehmender Abstraktionsfähigkeit geometrische Eigenschaften miteinander, wie z.B. das Quadrat als ein besonderes Rechteck. Lernende erfahren, dass geometrische Grundformen gebildet, verändert und verglichen werden können (Geobrett). Sie können erkennen, dass durch die Veränderung einer Seitenlänge die Grundform verändert wird. Lernende erstellen ebene Figuren auf Gitterpapier maßstäblich durch Verkleinern und Vergrößern. Entwicklung des Zeichnens Lernende wenden Bleistift, Lineal, Schablone, Geodreieck an, um ebene Figuren abzubilden. Dazu gehören freies Zeichnen von Linien, Nachzeichnen, Verbinden von Punkten durch Linien und Zusammenführen mehrerer Linien zu Grundformen. Lernende zeichnen Bögen und zueinander parallele oder senkrechte Geraden mit Zeichengeräten (u.a. Zirkel, Geodreieck). Lernende zeichnen ebene Figuren und Bauwerke in Gitter- und Punkterastern. PIKAS Zeichnen	Ich kann Dreieck, Kreis und verschiedene Vierecke erkennen und unterscheiden und benennen. Ich kann unterschiedliche Dreiecke, Kreise und Vierecke in meiner Umwelt entdecken und ihre Unterschiede beschreiben. Ich kann verschiedene Dreiecke und Vierecke mit einander vergleichen, indem ich die Länge der Seiten messe. Ich weiß, dass ein Rechteck mit vier gleichlangen Seiten ein besonderes Rechteck ist, das Quadrat genannt wird. Ich kann Figuren auf Gitterpapier verkleinern und vergrößern Ich kann mit unterschiedlichen Hilfsmitteln (Bleistift, Lineal, Geodreieck, Schablonen) Dreiecke, Rechtecke und Kreise nach Vorgabe oder eigenen Vorstellungen zeichnen. Ich kann Linien frei zeichnen und nachspuren. Ich kann mit Bleistift und Lineal Linien ziehen und Punkte verbinden. Ich kann mit dem Geodreieck Linien ziehen und parallele und senkrechte Geraden zeichnen.	Spuren herstellen (Fußabdrücke) Körper hinterlassen Spuren – flächige Abdrücke herstellen. Wo versteckt sich Geometrie? Lernende werden angeregt, geometrische Grund- und Flächenformen im Alltag zu finden: z.B. Verkehrszeichen, Dächer, Fenster, Türen, Verpackungen. Objekte sammeln, die rund, drei- oder viereckig sind, vergleichen Geometrisches Abbilden (Darstellen) Es werden Materialien bereitgestellt, die ein eigenständiges Erforschen der geometrischen Eigenschaften und deren Abbildungen und Verknüpfungen ermöglichen (Tangram, Pentominos, Streichholzvierlinge, Geobretter usw.) (s. Kaufmann 2010, S. 101-104). PRIMAKOM Zeichnen Am Geobrett werden geometrische Grundformen gebildet, verändert, verglichen. Die gleiche Eckenzahl verändert durch unterschiedliche Längen der Seiten die Grundform. App Geobrett: https://www.mathlearningcenter.org/apps/geoboard Beispiele PIKAS Eigenschaften von Formen Beispiele Primakom Ebene Figuren (Pikas Mathekartei 2022) und PIKAS Formen und Körper Weitere Anregungen unter „Stiftung kleine Forscher“ (2014) und Material Mathematik BMBF Verbindung zum Teilbereich Strukturen und funktionale Zusammenhänge (MSufZ). Lehrkräfte regen an, nach Mustern in Abbildungen, in Anordnungen und in der Umwelt zu suchen und diese nachzustellen, abzubilden, fortzusetzen. In Mathekonferenzen wird dies kommuniziert, dargestellt und verglichen. PIKAS Muster Zeichnen: App zum Zeichnen auf Punktepapier: https://dlgs.uni-potsdam.de/apps/isometriepapier PRIMAKOM Zeichnen: https://primakom.dzlm.de/inhalte/gr%C3%B6%C3%9Fen-und-messen/zeichnen/hintergrund
					Prozessbezogene Kompetenzen Verbindung zum Teilbereich Strukturen und funktionale Zusammenhänge Lernende benötigen für die Unterscheidung von Körpern und deren Abbildung (Darstellen) in geometrischen Grundformen Fachbegriffe, die in einem Wortspeicher mit mathematischen Begriffen gesammelt werden. Dadurch wird die Weiterentwicklung der Kompetenzen des Kommunizierens und des Argumentierens unterstützt. Folgende Begriffe werden erworben: Körper: Kugel, Würfel, Zylinder, Quader, Kegel Geometrische Grundformen: Kreis, Drei- und Viereck, Wortspeicher zum Vergleichen: Ecke, Seite, Fläche, Länge Lernende beschreiben Beziehungen zwischen den geometrischen Figuren (z.B. Viereck ist sogleich Rechteck und Quadrat, beide unterscheiden sich durch die Länge der Seiten) Modelle von Körpern werden hergestellt und untersucht. Lernende stellen Muster durch Legen und Fortsetzen her und erkennen Grundmuster. Sie identifizieren und beschreiben Grundmuster (Beziehung zum Kompetenzbereich MSufZ)	Ich habe Fachbegriffe gelernt und eingeprägt, die es mir ermöglichen die unterschiedlichen Körper und Figuren exakt zu benennen, zu beschreiben, zu vergleichen und mich mit Anderen darüber auszutauschen. Ich kann Gegenstände und Abbildungen von Gegenständen mit Begriffen wie rund, eckig, Anzahl der Ecken, der Kanten usw. so genau beschreiben, dass Andere verstehen, worüber ich spreche. Ich kann das Aussehen und die Funktionsweisen der verschiedenen Körper (Würfel. Quader usw.) miteinander vergleichen und ihre Unterschiede mit Hilfe von Fachbegriffen erklären.	Prozessbezogene Kompetenzen Lernende erhalten einen PIKAS Wortspeicher In Rechenkonferenzen können geometrische Grund- und Flächenformen entdeckt, dargestellt und verglichen werden (Kommunizieren, Darstellen, Argumentieren).
					Symmetrie Symmetrie kommt in der Natur und in der Umwelt vor. Sie ist Bestandteil von dekorativen oder technischen Mustern (Kunst, Architektur usw.), entsteht beim Basteln, Falten usw. (Beziehung zum Kompetenzbereich MSufZ). Lernende können durch die Auseinandersetzung mit Symmetrie das Verständnis des räumlichen Vorstellungsvermögens, das Erkennen von gegliederten Gestalten und Mustern sowie Erkenntnisse zur Funktionalität von symmetrischen Gegenständen entwickeln. Arithmetisches Wissen (Verdoppeln/Halbieren) wird unterstützt (Beziehung zum Kompetenzbereich ZuO). Symmetrieeigenschaften werden zunächst in Bezug auf die Achsensymmetrie erkundet. Symmetrische Muster können selbst entwickelt und fortgesetzt werden (Beziehung zum Kompetenzbereich MSufZ).	Ich kann in der Natur (z.B. Schmetterling, Spiegelungen im Wasser), an Gebäuden, in Kunstwerken, an Möbeln, an Geräten, auf Zahldarstellungen usw. Symmetrie entdecken. Ich empfinde symmetrische Formen oft als harmonisch. Ich weiß, was der Begriff Symmetrie bedeutet. Eine Figur ist symmetrisch, wenn die beiden Hälften einer Figur nach dem exakten mittigen Falten genau aufeinanderpassen. Ich weiß, dass die Faltlinie Symmetrieachse oder Spiegelachse genannt wird. Die Figuren, die durch Spiegelung oder Faltung entlang dieser Achse entstehen, werden achsensymmetrische Figuren genannt. Wenn ich mich oder Gegenstände im Spiegel anschaue, sehe ich mein Spielbild oder die Spiegelbilder der Gegenstände. Original und Spiegelbild verhalten sich spiegelverkehrt zueinander, sie sind symmetrisch oder ganz genau gesagt: achsensymmetrisch. Ich kann mit dem Spiegel prüfen, ob eine Figur aus symmetrischen Teilen besteht. Wenn der Spiegel auf der Spiegelachse steht, sieht die Figur im Spiegel genauso aus, wie die durch ihn verdeckte Hälfte. Ich kann Faltschnitte herstellen und mit ihrer Hilfe die Eigenschaften achsenymmetrischer Figuren erkunden, prüfen und beschreiben. Ich weiß, dass die Flächentreue ein Merkmal symmetrischer Figuren ist. Ich lege die Teilfiguren vom Faltschnitt aufeinander und prüfe, ob sie genau aufeinanderpassen. So erkunde ich, ob Flächentreue vorliegt. Ich weiß, dass die Längentreue ein weiteres Merkmal symmetrischer Figuren ist. Dazu prüfe ich durch Messung, ob der Abstand zwischen gegenüberliegenden Kanten der Teilfiguren zur Symmetrieachse gleich groß ist. Beim Vergleich der Teilfiguren, die durch Faltschnitte entstehen, erkenne ich, dass diese sich spiegelverkehrt zueinander verhalten. Diese Eigenschaft symmetrischer Figuren ist mir schon durch Erkundungen mit einem Spiegel bekannt. Ich kann Symmetrieachsen in Figuren einzeichnen, z.B. senkrecht in die Mitte von einem Herz. Wenn ich dann an der Symmetrieachse falte, sind beide Hälften deckungsgleich, sie passen exakt aufeinander, sind also symmetrisch. Ich kann auch in meiner Vorstellung entlang einer gedachten Symmetrieachse eine Figur in Gedanken falten und so in der Vorstellung prüfen, ob eine Figur aus symmetrischen Teilen besteht Ich weiß, dass es Figuren mit mehreren Symmetrieachsen (Spiegelachsen) gibt, die ich entdecken und einzeichnen kann. In einem Quadrat z.B. kann ich 4 Symmetrieachsen entdecken (senkrecht, waagerecht, zwei in den Diagonalen), in einem Rechteck zwei, in einem Kreis unendlich viele. Ich weiß, dass die Symmetrie für die Funktion von vielen Gegenständen bedeutsam ist. Z.B. funktioniert eine Schaukel nur dann perfekt, wenn die die beiden Seile gleichlang, also achsensymmetrisch zueinander angeordnet sind.	Symmetrie Lernende erforschen Symmetrie in der Natur und Umgebung. Symmetrieachsen werden z.B. durch Faltschnitte und die Nutzung von Spiegeln verdeutlicht. Übersicht über Kontinuität im Unterricht hinsichtlich der Symmetrieeigenschaften: PIKAS Kompetenzaufbau im Kontext „Symmetrie“ Anregungen für den Unterricht unter PIKAS: Symmetrie in der Grundschule https://didaktik.mathematik.hu-berlin.de/files/ausgewkap-geomabbgrundsch.pdf
					Prozessbezogene Kompetenzen: Lernende können sich durch das Herstellen symmetrischer Figuren und die Analyse vorgegebener symmetrischer Figuren über die damit gemachten Erfahrungen austauschen (Darstellen, Argumentieren, Kommunizieren). Eigenschaften und Relationen von Figuren untereinander werden thematisiert (Modellieren). Der Wortspeicher wird in Anwendung aufgebaut und erweitert: Hälften, Achse, Gerade, Spiegeln, Faltkante usw. Grundlegende Informationen finden sich bei PRIMAKOM Symmetrie in der Grundschule PIKAS Kompetenzaufbau im Kontext „Symmetrie“	Bei den Erkundungen mit einem Spiegel, Faltungen und Faltschnitten entdecke ich die Eigenschaften von achsensymmetrischen Figuren, die ich dokumentiere und in der Lerngruppe präsentiere. Wir besprechen in der Lerngruppe mögliche Vorgehensweisen zur Prüfung von Symmetrie und diskutieren die Vor- und Nachteile der unterschiedlichen Vorgehensweisen. Ich habe viele neue Fachbegriffe (z.B. Hälfte, Gerade, Symmetrieachse, Faltkante, Spiegeln, Flächentreue, Längentreue usw. erworben, die es mir ermöglichen, die Ergebnisse meiner Erkundungen der Symmetrie exakt zu beschreiben, zu dokumentieren und mich mit anderen darüber auszutauschen.	Prozessbezogene Kompetenzen Um die Fähigkeiten zur Problemlösung, Modellierung, Darstellung, Kommunikation usw. zu erweitern werden entsprechende Aufgabenstellungen angeboten, in denen die Lernende selbsttätig und in Gruppen arbeiten. Beispiele: PIKAS Gute Aufgaben im Geometrie-Unterricht Anregungen in Lerndokumentation Mathematik (2009, S. 51 – 94)
					Parallele, Senkrechte, Mittelsenkrechte Erkennen und Beschreiben: Die Lernenden finden in ihrer Umgebung parallele und zueinander senkrechte Linien, verwenden die Grundbegriffe: Punkt, Gerade, Strecke, Winkel, Abstand, Radius, parallel, senkrecht, zur Beschreibung ebener und räumlicher Figuren, können beschreiben, dass eine Mittelsenkrechte ein Gerade ist, die senkrecht auf einer Strecke steht und diese in der Mitte teilt. Alle Punkte auf der Mittelsenkrechten sind von den beiden Endpunkten der Strecke gleich weit entfernt.	Ich kann zueinander parallele und zueinander senkrechte Linien in meiner Umgebung finden. Ich kenne die Begriffe Punkt, Gerade, Strecke, Winkel, Abstand, Radius, parallel, senkrecht und kann sie verwenden. Ich kenne besondere Linien wie die Mittelsenkrechte.	Konstruktionsanleitungen - lesen und schreiben - Konstruktionsdiktate à kommunizieren Begriffsbildung: Sprachspeicher Beschriftungen von Konstruktionen sorgfältig einführen, z.B. Punkte mit Großbuchstaben beschriften
					Darstellen und Konstruieren: – Die Lernende konstruieren ebene Figuren (parallele und senkrechte Geraden, Winkel, Rechtecke, Quadrate, Kreise, Mittelsenkrechte).	Ich kann mit dem Geodreieck und Lineal und Zirkel zueinander parallele und zueinander senkrechte Linien, Rechtecke, Quadrate und Kreise zeichnen. Ich kann die Mittelsenkrechte einer Strecke konstruieren.	Parallelen, Senkrechte und Mittelsenkrechte können gefaltet werden. Dabei lassen sich Kanten, Geraden, Strecken, Punkte, rechte Winkel, usw. entdecken (siehe Rasch & Sitter, 2017, S. 21-26). Konstruktionen mit GeoGebra https://www.geogebra.org/m/nhbkxwgs
					Winkel, Winkelhalbierende Die Lernenden verwenden die Grundbegriffe: Schenkel, Scheitel(-punkt), Winkelmaß, Winkelhalbierende. Die Lernenden kennen die unterschiedlichen Größenbereiche von Winkeln und können diese bestimmen: Nullwinkel, spitzer Winkel, rechter Winkel, stumpfer Winkel, gestreckter Winkel, überstumpfer Winkel, Vollwinkel, erkennen Winkelpaare: Nebenwinkel, Scheitelwinkel, Stufenwinkel, Wechselwinkel. Die Lernenden können beschreiben, dass eine Winkelhalbierende ein Gerade ist, die einen Winkel in zwei Hälften teilt. Alle Punkte auf der Winkelhalbierenden sind von den beiden Schenkeln gleich weit entfernt, konstruieren eine Winkelhalbierende, konstruieren Winkel, messen Winkel, zeichnen Winkel.	Ich kenne die Begriffe Schenkel, Scheitel(-punkt), Winkelmaß, Winkelhalbierende und kann sie bei der Konstruktion von Winkeln anwenden.Ich kann Winkel ordnen und benennen: Nullwinkel, spitzer Winkel, rechter Winkel, stumpfer Winkel, gestreckter Winkel, überstumpfer Winkel, Vollwinkel. Ich kann Winkel benennen, die entstehen, wenn sich zwei Geraden schneiden. Ich kann Winkel benennen, die entstehen, wenn eine Gerade zwei parallele Geraden schneidet.Ich kann eine Winkelhalbierende konstruieren, erklären was das ist und die Konstruktionsschritte beschreiben. Ich kann Winkel konstruieren. Ich kann Winkel mit dem Geodreieck messen. Ich kann Winkel mit dem Geodreieck zeichnen.	Winkelplakat erstellen, auf dem die Begriffe den Abbildungen zugeordnet sind. In GeoGebra können die Winkelmaße angezeigt werden. Die Lernenden können beobachten, wie sich die Winkelmaße ändern, wenn die Geraden verschoben werden. Mögliche Beobachtungshinweise: Welche Winkel sind immer gleich groß? Welche Winkel ergeben zusammen 180°? https://www.geogebra.org/m/UqxuRJ9X
					Dreiecke Dreiecke klassifizieren: Die Lernenden können Dreiecke: nach ihren Winkeln klassifizieren: spitzwinklig, rechtwinklig, stumpfwinklig, nach ihren Seiten klassifizieren: gleichseitige, gleichschenklige, allgemeine Dreiecke. Dreiecke konstruieren: Die Lernenden können rechtwinklige Dreiecke mit dem Geodreieck konstruieren, gleichschenkliche Dreiecke konstruieren, indem sie die Mittelsenkrechte konstruieren. Die Lernenden können konstruierte Dreiecke mit Fachwörtern (Basis, Schenkel) beschreiben, verwenden gegebene Winkel- und Seitenmaße, kennen die Kongruenzsätze.	Ich kann Dreiecke nach ihren Winkeln sortieren und sagen, ob es sich um ein spitzwinkliges, rechtwinkliges oder stumpfwinkliges Dreieck handelt. Ich kann Dreiecke nach ihren Seitenverhältnissen sortieren und sagen, ob es sich um ein gleichseitiges, gleichschenkliges oder allgemeines Dreieck handelt. Ich kann rechtwinklige Dreiecke mit dem Geodreieck konstruieren. Ich kann gleichschenklige Dreiecke konstruieren, indem ich von einer Strecke die Mittelsenkrechte konstruiere. Bei der Beschreibung des Vorgehens verwende ich die Begriffe Basis und Schenkel. Ich weiß welche Seiten und Winkel gegeben sein müssen, um Dreiecke eindeutig zu konstruieren (Kongruenzsätze) und kann es konstruieren	Arbeit mit konkreten Materialien: Dreiecke nach ihren Eigenschaften sortieren. Dreiecke mit unterschiedlichen Winkeln lassen sich konstruieren, indem die Dreiecksspitze C verändert wird. Gleichschenklige Dreiecke können mit Hilfe des Achsenkreuzes gezeichnet werden (siehe Rasch & Sitter, 2017, 29-32). Gleichseitige Dreiecke aus Papierstreifen falten: https://www.mathematische-basteleien.de/dreieck.htm Unterrichtsideen zu den Kongruenzsätzen: https://unterrichten.zum.de/wiki/Kongruenz_von_Dreiecken
					Anwenden: Die Lernenden untersuchen Fragen der Lösbarkeit und Lösungsvielfalt von Konstruktionsaufgaben und formulieren diesbezüglich Aussagen, führen Beweise am Dreieck durch z.B. Innenwinkelsumme.	Ich kann zu Aufgaben mit Winkeln, Strecken, Geraden und Dreiecken eine Vermutung über Zusammenhänge formulieren und so beschreiben, dass andere sie verstehen. Ich kann die Innenwinkelsumme und Außenwinkelsumme am Dreieck beweisen.
					Entdeckungen und Berechnungen am Dreieck Satz des Thales Die Lernenden kennen den Satz des Thales und die dafür nötigen Voraussetzungen, können den Satz des Thales nutzen, um Winkel zu bestimmen und konstruieren, beweisen mit dem Satz des Thales am Dreieck. Mittelpunkte vom Dreieck Die Lernenden konstruieren verschiedenen Mittelpunkte im Dreieck: Inkreis-, Umkreismittelpunkt und Schwerpunkt, können die Konstruktion der verschiedenen Mittelpunkte beschreiben.	Ich kenne den Satz des Thales und kann erklären, unter welchen Voraussetzungen er gilt. Ich kann den Satz des Thales nutzen, um unbekannte Winkel zu bestimmen und um rechte Winkel zu konstruieren. Ich kann Beweise mit dem Satz des Thales führen. Ich kenne die verschiedenen Mittelpunkte im Dreieck und kann sie konstruieren: Inkreis-, Umkreismittelpunkt und Schwerpunkt. Ich kann eine Konstruktionsbeschreibung zu den Mittelpunkten so erstellen, dass sie nachvollziehbar und übersichtlich ist.	Satz des Thales Den Satz des Thales entdecken: Die Lernenden zeichnen eine Strecke, die die Hypotenuse darstellt, und mit Hilfe eines rechteckigen Gegenstands (Postkarte, CD-Hülle) möglichst viele rechtwinklige Dreiecke. Der rechte Winkel liegt über der Hypotenuse. Wenn sie die möglichen Eckpunkte verbinden, entsteht annähernd ein Halbkreis. In GeoGebra: Rechtwinkliges Dreieck konstruieren und einstellen, dass die Ecke im rechten Winkel eine Spur hinterlässt. Weitere Ideen: https://www.mnu.de/weko/5-2_thales.pdf Mittelpunkte vom Dreieck Eine Lernumgebung mit Aufgaben zum Konstruieren und Entdecken ist im Schulbuch „Mathewerkstatt 7“.
					Satz des Pythagoras Die Lernenden verstehen den Satz des Pythagoras und seine Voraussetzungen, wenden den Satz des Pythagoras an und berechnen fehlende Größen, begründen und Beweisen mithilfe des Satz des Pythagoras	Ich kann den Satz des Pythagoras in eigenen Worten wiedergeben, dabei auch die Voraussetzung deutlich benennen. Ich kann Streckenlängen mit Hilfe des Satzes des Pythagoras berechnen. Ich kann erklären, wie man mit Hilfe der Umkehrung des Satzes des Pythagoras rechte Winkel finden kann.	Zum Satz des Pythagoras gibt es viel Unterrichtsmaterial. Zur Vertiefung eignet sich das Nachvollziehen von Beweisen, z.B. https://www.schule-bw.de/faecher-und-schularten/mathematisch-naturwissenschaftliche-faecher/mathematik/unterrichtsmaterialien/sekundarstufe1/geometrie/pyth/beweise
					Strahlensätze Die Lernenden erkennen Strahlensätze und wissen, wann diese angewendet werden können, können die Verhältnisgleichung angeben, berechnen Streckenlängen mithilfe der Strahlensätze.	Ich kann erkennen, wann die Strahlensätze angewendet werden können Ich kann die Verhältnisgleichung angeben. Ich kann Streckenlängen mit Hilfe der Strahlensätze berechnen	Erläuterungen und Begründungen an Skizzen, wann man die Strahlensätze anwenden kann.
					Trigonometrie Die Lernenden wenden Sätze der ebenen Geometrie (insbesondere trigonometrische Beziehungen) bei Konstruktionen, Berechnungen, Begründungen und Beweisen an, auch mit Hilfe digitaler Mathematikwerkzeuge. Sie können Steigungswinkel der Hypotenuse im Dreieck berechnen, wenn zwei Seiten gegeben sind, können in rechtwinkligen Dreiecken aus den Angaben einer Seitenlänge und einer weiteren Größe alle anderen Winkel und alle anderen Seitenlängen bestimmen, können mit dem Taschenrechner zu einem vorgegebenen Winkel α die Werte sin α, cos α und tan α bestimmen und umgekehrt aus diesen Werten den Winkel, können in verschiedenen Situationen mit sin α, cos α und tan α weitere Werte berechnen, können am Beispiel der Höhenveränderung in einem rechtwinkligen Dreieck erklären, was eine Sinusfunktion ist können Situationen benennen, die sich durch eine Sinusfunktion beschreiben lassen, können eine fehlende Winkelgröße im Dreieck ausrechnen.	Ich kann Steigungswinkel der Hypotenuse im Dreieck berechnen, wenn zwei Seiten gegeben sind. Ich kann in rechtwinkligen Dreiecken aus den Angaben einer Seitenlänge und einer weiteren Größe alle anderen Winkel und alle anderen Seitenlängen bestimmen. Ich kann mit dem Taschenrechner zu einem vorgegebenen Winkel α die Werte sin α, cos α und tan α bestimmen und umgekehrt aus diesen Werten den Winkel. Ich kann in verschiedenen Situationen mit sin α, cos α und tan α weitere Werte berechnen. Ich kann am Beispiel der Höhenveränderung in einem rechtwinkligen Dreieck erklären, was eine Sinusfunktion ist. Ich kann Situationen benennen, die sich durch eine Sinusfunktion beschreiben lassen. Ich kann eine fehlende Winkelgröße im Dreieck ausrechnen.	Sinus und Kosinus können über (ähnliche) rechtwinklige Dreiecke, bei denen die Seitenverhältnisse untersucht werden, eingeführt werden. Ideen dazu im Schulbuch „Mathewerkstatt 10“. In GeoGebra gibt es Animationen, die zeigen, wie sich Sinus und Kosinus verändern, wenn der Winkel am Einheitskreis verändert wird, z.B. https://www.geogebra.org/m/FJtrEDAr
					Symmetrien Die Lernenden beschreiben ebene und räumliche Figuren mit den Begriffen achsensymmetrisch und punktsymmetrisch, verändern nahezu spiegelsymmetrische Figuren so, dass sie spiegelsymmetrisch sind. geben an, wie viele Spiegelachsen ein Bild hat. führen Spiegelungen an Geraden durch, konstruieren die Spiegelachse zwischen kongruenten Figuren, kennen Eigenschaften von Achsenspiegelungen: längentreu, geradentreu, parallelentreu, flächeninhaltstreu, winkelgrößeninvertierend, kennen die Symmetrien in Kreisen.	Ich kann bei der Beschreibung von ebenen Figuren und Körpern die Begriffe achsensymmetrisch und punktsymmetrisch verwenden. Ich kann fast spiegelsymmetrische Bilder so abändern, dass sie spiegelsymmetrisch sind. Ich kann angeben, wie viele Spiegelachsen ein Bild hat. Ich kann Figuren an Geraden spiegeln. Ich kann die Spiegelachse zwischen zwei gespiegelten Figuren einzeichnen. Ich kennen die Eigenschaften von Achsenspiegelungen: längentreu, geradentreu, parallelentreu, flächeninhaltstreu, (winkelgrößeninvertierend). Ich weiß, dass Kreise sowohl spiegel- als auch drehsymmetrisch sind.	Spiegelung von Figuren an Geraden: Auf Kästchenpapier können Geradentreue und Parallelentreue gut verdeutlicht werden.
					Drehungen Die Lernenden geben an, ob ein Bild drehsymmetrisch ist, und geben den Drehpunkt an, bestimmen den Drehpunkt bei kongruenten Figuren, kennen Eigenschaften von Drehungen, führen Drehungen um vorgegebene Gradzahl durch, Können angeben, ob zwei kongruente Figuren durch eine Verschiebung, eine Spiegelung oder eine Drehung auseinander hervorgehen.	Ich kann erkennen, ob ein Bild drehsymmetrisch ist und den Drehpunkt angeben. Ich kann den Drehpunkt von zwei kongruenten Figuren bestimmen. Ich kenne die Eigenschaften von Drehungen. Ich kann eine Drehung um eine gegebene Gradzahl zeichnen. Ich kann angeben, ob zwei kongruente Figuren durch eine Verschiebung, eine Spiegelung oder eine Drehung auseinander hervorgehen.	Puzzlespiel, z.B. Ubongo oder mit Pentominos: Teile werden gedreht, verschoben und gespiegelt (wenn ich ein Teil umdrehe). Um Drehpunkte zeichnerisch zu bestimmen, müssen die Lernenden noch wissen, wie Mittelsenkrechten konstruiert werden.
					Verschiebungen Die Lernenden erkennen Verschiebungen, führen Verschiebungen durch, kennen die Eigenschaften von Verschiebungen.	Ich kann Verschiebungen erkennen. Ich kann Verschiebungen zeichnen. Ich kann die Eigenschaften von Verschiebungen benennen und erklären.	Werden Verschiebungen mit Hilfe von Schablonen gezeichnet, ist darauf zu achten, dass die Figuren nicht gedreht werden.
					Symmetrien, Drehungen, Verschiebungen, Kongruenz Die Lernenden erfassen und begründen Eigenschaften von Figuren mit Hilfe von Symmetrie, einfachen Winkelsätzen oder der Kongruenz.	Ich kann bestimmen, ob zwei Figuren kongruent sind und das begründen, indem ich mich auf die Kongruenzsätze oder die Eigenschaften von Drehungen, Verschiebungen und Spiegelungen beziehe.	https://www.studienkreis.de/mathematik/kongruenz-aehnlichkeit-figuren/
					Vergrößern und Verkleinern - Zentrische Streckung Die Lernenden erkennen mathematisch ähnliche Figuren, beschreiben die Beziehungen zwischen Winkeln und Seiten in ähnlichen Figuren. vergrößern und verkleinern einfache Figuren maßstabsgetreu, rechnen die Länge beim Vergrößern und Verkleinern mit einem gegebenen Maßstab um, vergrößern und verkleinern Figuren von einem Punkt aus, bestimmen die Vergrößerungs- bzw. die Verkleinerungszahl, bestimmen den Maßstab, auch mit Einheitenwechsel, vergrößern und verkleinern, indem sie mit geeigneten Zahlen multiplizieren, berechnen beim Skalieren die Veränderung von Flächen und Volumina.	Ich kann erklären, wann zwei Figuren zueinander mathematisch ähnlich heißen. Ich kann beschreiben, welche Beziehungen für Winkel und Seitenverhältnisse in ähnlichen Figuren gelten. Ich kann Figuren mit einer vorgegebenen Zahl vergrößern oder verkleinern und kann erklären, wie man dabei vorgeht. Ich kann die Längen beim Vergrößern und Verkleinern mit einem gegebenen Maßstab umrechnen. Ich kann eine Figur zeichnerisch von einem Punkt aus vergrößern und verkleinern. Ich kann die Vergrößerungs- bzw. die Verkleinerungszahl finden, wenn ich ein Original mit einem dazu gehörigen Bild vergleiche. Ich kann bei der Verkleinerung sehr großer Gegenstände in mehreren Schritten den Maßstab bestimmen und dabei auch mit dem Wechsel von Einheiten umgehen. Ich kann vergrößern und verkleinern, indem ich geeignet mit verschiedenen Zahlen multipliziere. Ich kann berechnen, wie sich beim Skalieren die Flächeninhalte und Volumina verändern.	Die Hinführung zur zentrischen Streckung beginnt bereits mit dem Verkleinern und Vergrößern mit Hilfe von Kästchenpapier.
					Figuren und Körper Die Lernenden benennen und identifizieren Figuren und Körper: Rechteck, Quadrat, Parallelogramm, Dreieck, Quader, Würfel, Zylinder, Pyramide, Kegel, Kugel, benennen Eigenschaften von Vielecken und erkennen Gemeinsamkeiten und Unterschiede,charakterisieren Vierecke mittels passender Ober- und Unterbegriffe, auch anhand von Beispielen, analysieren und klassifizieren geometrische Objekte der Ebene (insbesondere Winkel, Dreiecke, Vierecke) und des Raumes (insbesondere Prismen, Pyramiden, Zylinder, Kegel, Kugel), benennen und beschreiben geometrische Objekte und Beziehungen in der Umwelt mit Hilfe mathematischer Modelle (Punkte, Winkel, Strecken, Geraden, Flächen, Körper) und ihre Zusammenhänge.	Ich kann Rechtecke, Quadrate, Rauten, Drachen, Trapeze, Parallelogramme im Alltag erkennen und richtig benennen. Ich kann Zylinder, Pyramiden, Kegel und Kugeln im Alltag erkennen und richtig benennen. Ich kann Eigenschaften von Vielecken benennen, Gemeinsamkeiten und Unterschiede erkennen. Ich kann zu Vierecken passende Ober- und Unterbegriffe benennen, d.h. Ich erkenne auch ein Rechteck als Trapez. Auch in Alltagssituationen kann ich an Beispielen erklären, was ein Ober- oder Unterbegriff ist. Ich kann geometrische Objekte der Ebene und des Raumes analysieren und nach ihren Eigenschaften sortieren. Ich kann Objekte aus meiner Umgebung mit Hilfe von Punkten, Linien, Winkel, Flächen oder Körpern beschreiben, und erklären wie diese zusammenhängen.	Sprachspeicher Körper als Material untersuchen. Körper herstellen, z.B. mit Knete oder Kantenmodelle. Haus der Vierecke https://primakom.dzlm.de/primafiles/uploads/Dokumente/EbeneFiguren_Hintergrund_Tabelle%20Haus%20der%20Vierecke.pdf
					Körper: Schrägbilder und Netze Erkennen und Beschreiben: Die Lernenden erkennen anhand eines Netzes, welcher bzw. ob ein Körper entsteht, verwenden die Begriffe: Prisma, Zylinder, Kante, Körperhöhe, Seitenhöhe, Raumdiagonale, skizzieren Schrägbilder, entwerfen Netze, stellen Körper her von: Würfeln, Quadern, Zylindern, Pyramiden, Kegeln, Prisma, fertigen Netze, Schrägbilder und Modelle digital und analog an, bestimmen unbekannte Längen in Körpern mithilfe geometrischer Sätze und Formeln.	Wenn ich ein Netz sehe, kann ich mir in Gedanken vorstellen, wie der Körper dazu aussieht oder ob gar kein Körper daraus entstehen kann. Ich kann Körper mit Fachwörtern (Prisma, Zylinder, Kante, Körperhöhe, Höhe einer Seitenfläche, Raumdiagonale) beschreiben. Ich kann einen Körper im Schrägbild und Netz zeichnen, z.B. Würfeln, Quadern, Zylindern, Pyramiden, Kegeln, Prisma. Ich kann Netze, Schrägbilder und Modelle digital erstellen. Ich kann unbekannte Längen in Körpern bestimmen und dazu geometrische Sätze (Ähnlichkeitssätze, Satz des Pythagoras) oder Formeln (für Volumen, Oberflächeninhalt) nutzen.	Mit der App Klippklapp werden Würfelnetze erstellt und eingefärbt bzw. zu vorgegebenen Netzen entschieden, ob es sich um Würfelnetze handelt oder nicht: https://dlgs.uni-potsdam.de/apps/klipp-klapp Körper, die sich ausklappen und wieder zusammenfalten lassen oder Polydron-Bausteine. Mit der App Isometriepapier können isometrische Darstellungen erstellt werden. Es kann frei gezeichnet werden: https://dlgs.uni-potsdam.de/apps/isometriepapier
					Kopfgeometrie (gedankliche Anwendung) Die Lernenden entwickeln Vorstellungen im zwei- und dreidimensionalen Raum, operieren (z.B. verschieben, drehen, spiegeln) gedanklich mit im Raum enthaltenen Objekten (Punkten, Strecken, Flächen und Körpern).	Ich kann mir Dinge im zwei- und dreidimensionalen Raum gut vorstellen. Ich kann Objekte im Raum gedanklich verschieben, drehen oder spiegeln.	Die Aufgaben des Wettbewerbs „Känguru der Mathematik“ umfassen meist auch viele Kopfgeometrieaufgaben. Aufgaben der vergangenen Jahre: https://www.mathe-kaenguru.de/
					Längen-, Flächen- und Volumenmessungen und weitere Größen wie Winkel und Zeitspannen sind dem Bereich Größen und Messen zugeordnet.

Zum Inhaltsverzeichnis zurück

Tabelle 3.4: Daten und Zufall

Abkürzungen Tabellen: b = basal | e = elementar | p = primär | s = sekundär


Teilbereich: Daten und Zufall (DuZ)
					Muster, Strukturen und funktionaler Zusammenhang Lernende lernen im Teilbereich Daten und Zufall einfache kombinatorische Fragestellungen durch systematisches Probieren und Vorgehen zu lösen. Sie erkennen Gesetzmäßigkeiten wie funktionale Beziehungen, Sortierungen und Ordnungen beim Erstellen von Übersichten mit Hilfe von Abbildungen (Tabellen, Strichlisten usw.) (vgl. KMK 2022, S. 13 - 18). Die Ergebnisse werden hinterfragt, beschrieben und erklärt (mathematisch kommuniziert) und bei Bedarf weiterentwickelt).			Pädagogische Angebote Lehrkräfte regen an, kombinatorische Fragestellungen zu entwickeln und Daten zu sammeln. Für das systematische Probieren und Vorgehen sowie das Vergleichen, werden Tabellen, Skizzen, Diagramme erarbeitet, durch die Lösungen dargestellt, beschrieben und kommuniziert werden können.
b	e	p	s	ILZ	Stufe in Erwachsenensprache	Stufe in Kindersprache	Lernbausteine
				1	Sinnliche Welterkundung Allgemein-mathematische (prozessbezogene) Kompetenzen basieren auf einer aktiv-entdeckenden Auseinandersetzung durch Zufallshandlungen mit Dingen/Gegenständen Inhaltsbezogene mathematische Vorerfahrungen Die Lernenden handeln zufällig in ihrem Körper- und Nahfeld. Durch die Komplexität der Situation können sie basale Erfahrungen in den sich überschneidenden Kompetenzbereichen machen. Die Gestaltung des Nah- und Greiffelds ermöglicht ihnen das Lernen durch Berühren, Bewegen, Beobachten interessanter Eigenschaften und Merkmale: Raumerfahrungen durch Lagerungsorte (Rollstuhl, Little Room usw.), Raumbegrenzungen, räumliche Anordnung von Dingen (oben- unten, vorne – hinten, innen – außen) sind bedeutsam für den Kompetenzbereich Raum und Form (RuF), basale Vorerfahrungen durch regelmäßige und wiederholte zeitliche Abläufe und räumliche Angebote sind bedeutsam für die Kompetenzbereiche Muster, Strukturen und funktionale Zusammenhänge (MSufZ) sowie Daten und Zufall (DuZ), sinnliche Erfahrungen durch die Beschaffenheit von Dingen (einschließlich Geruch und Geschmack) mit weiteren unterschiedlichen Eigenschaften und Merkmalen (hart – weich, farbig, glatt, laut – leise, hell – dunkel usw.) Formen (rund – eckig) sind bedeutsam für den Kompetenzbereich Raum und Form (RuF), Erfahrungen bei den Zufallshandlungen mit Gewicht, Größe, Entfernung (groß – klein, leicht – schwer, nah – weit) sind bedeutsam für den Kompetenzbereich Größen und Messen (GuM) Die benannten Erfahrungen ermöglichen die Entwicklung der Fähigkeit, Dinge grundsätzlich zu unterscheiden. Das ist wiederum eine Voraussetzung für das Bilden von Mengen (Sortieren) im Kompetenzbereich Zahl und Operation (ZuO)	Die Ausdrucksformen der Lernenden in den basalen Stufen sind überwiegend nonverbal. Die Formulierungen dienen der Einnahme der Perspektive von Lernenden. Ich kann, was um mich geschieht hören, sehen, spüren, riechen, schmecken, fühlen. Ich kann die Dinge, die ich zufällig ergreife, berühren, belecken und in Bewegung bringen. Dabei erfahre ich, dass sich Gegenstände und Materialien unterschiedlich anfühlen. Ich beginne, ganz bestimmte Personen, Gegenstände und Materialien, Muster, Formen zu bevorzugen und kann dies durch Zuwendung, Wiederholung, durch Mimik, Gestik und durch Laute zum Ausdruck bringen.	Gestaltung des Nah- und Greiffelds: Materialien und Gegenstände sind im Nah- und Greiffeld angebracht, die leicht berührt und bewegt werden können die Geräusche oder Lichteffekte auslösen die kontrastreiche Muster und Farben haben die aus unterschiedlichen Formen und Materialen bestehen Handlungen werden von Bezugspersonen und anderen Lernenden beobachtet und im Dialog gespiegelt. Beispiele in Hehn-Oldiges/Simon 2022 (Datei verlinken) Materialien, die zu aktiven Wiederholungen anregen, werden gezielt angeboten und durch weitere, mit ähnlichen Eigenschaften ergänzt. …
				2	Welterkundung durch unspezifisches Operieren Aktive Wiederholungen erweitern die allgemein-mathematische Kompetenzen durch die aktiv-entdeckenden Auseinandersetzung mit Dingen/Gegenständen Inhaltsbezogene mathematische Vorerfahrungen Interessante Effekte durch Dinge und Materialien im Körper-, Nah- und Greiffeld werden von den Lernenden aktiv wiederholt und die inhaltsbezogenen Vorerfahrungen zu den Kompetenzbereichen (MSufZ, RuF, GuM, ZuO, DuZ) können sich jeweils festigen und erweitern. Dinge/Gegenstände werden mit dem Mund, den Händen oder Füßen erkundet (Berühren, Klopfen, Werfen usw.). Erreichbare Materialien und Dinge ermöglichen so die aktive Wahrnehmung und zunehmende Unterscheidung von Gegenständen und deren Eigenschaften: Größe, Beschaffenheit, Form, Farbe, Klangeffekte, Geruch, Geschmack usw.	Ich kann Bewegungen, die es mir ermöglichen, für mich bedeutsame Dinge zu erreichen oder Effekte herbeizuführen, aktiv wiederholen. Ich kann diese Dinge mit dem Mund, den Händen und den Füßen durch Berühren, Klopfen, Werfen usw. immer genauer erkunden und so Größe, Beschaffenheit, Form, Farbe, Klangeffekte, Geruch, Geschmack usw. wahrnehmen. Ich kann meine Handlungen wiederholen und erfahre dadurch, dass sich die Gegenstände und Dinge in meiner Umgebung unterschiedlich anfühlen, dass sie unterschiedlich aussehen, riechen, schmecken, klingen usw.	Gestaltung des Nah- und Greiffelds: Bevorzugte Gegenstände, Materialien werden so angebracht, dass sie erreichbar sind und aktive Wiederholungen ermöglichen. Zeit für die selbsttätige Erkundung des Nah und Greiffeldes wird zur Verfügung gestellt. Empfohlen wird z.B. die Lagerung in Rückenlage auf einem Resonanzbrett, auf dem Materialien getastet werden können. Das Resonanzbrett verstärkt akustische Effekte und animiert zur Erkundung. Im Stehständer werden Materialien im Greiffeld angebracht, die durch die aktiven Wiederholungen Spür-, Seh- und Höreindrücke auslösen und die Aufmerksamkeit anregen.
				3	Spezifisches Hantieren erweitert die allgemein-mathematischen Kompetenzen durch die gezieltere aktiv-entdeckende Auseinandersetzung mit Dingen/Gegenständen und deren Funktion Inhaltsbezogene mathematische Vorerfahrungen Die Lernenden erkunden gezielt Dinge/Gegenstände und Materialien in ihrer unmittelbaren Umgebung und wenden als bewährt erfahrene Handlungsschemata (Lecken, Beißen, Klopfen, Werfen, Fallenlassen usw.) an. Auf diese Weise erfahren sie deren unterschiedlichen Eigenschaften (Vorerfahrungen für die Kompetenzbereiche GuM, ZuO), deren räumliche Anordnungen (Vorerfahrungen für die Kompetenzbereiche RuF) und die Veränderbarkeit von Mengen (Teile-Ganzes-Schema) (Vorerfahrungen für die Kompetenzbereiche ZuO). Die funktionsbezogene Nutzung ist noch nicht erschlossen. Als bewährt erfahrene Handlungsschemata werden auf Neues angewendet (Lecken, Beißen, Klopfen, Werfen, Fallenlassen usw.). Die Unterschiede in den Dingen/Gegenständen und Materialien, mit denen hantiert wird, führen zu neuen Erfahrungen.	Ich kann Materialien und Gegenstände mit dem Mund, den Augen und den Händen gezielter erkunden. Ich kann die dabei erprobten Handlungen (Lecken, Beißen, Fallenlassen…) zur Erkundung noch unbekannter Gegenstände anwenden. Ich kann beobachten, wie andere Menschen mit den Gegenständen umgehen und beginne dadurch wahrzunehmen, wie diese genutzt werden. Ich lerne, dass nicht alle meine erprobten Handlungsweisen für jeden Gegenstand geeignet sind. Ich beginne, Gegenstände durch bestimmte Merkmale als zueinander zugehörig wahrzunehmen.	Gestaltung des Handlungsfelds: Der Arbeitsbereich ist so zu gestalten, dass mit den darin erreichbaren Gegenständen hantiert werden kann (abgegrenzter räumlicher Bereich, Multifunktionstisch MFA-Tisch, Tastbretter, Materialkisten). Für das zunächst noch nicht an den Funktionen orientierte Erkunden durch Lecken, Beißen, Klopfen, Werfen usw. müssen Gegenstände und Materialien robust und stabil sein. Dadurch wird und ermöglicht, dass die unterschiedlichen Eigenschaften untersucht werden können. Materialkisten (ermöglichen Vorerfahrungen in den Bereichen GuM, ZuO) und verschiedene Behältnisse (ermöglichen Vorerfahrungen im Bereich RuF) werden zeitlich und räumlich verlässlich zur Verfügung gestellt (DuZ, RuF, MSufZ). Sie können ausgeleert und eingeräumt werden können. Mengen können umgefüllt, verändert und sortiert werden (Multifunktionstisch (MFA-Tisch n. Nielsen) (bedeutsam für die Kompetenzbereiche ZuO, MSufZ, RuF). Tastbretter mit daran befestigtem Material ermöglichen eine intensive Beschäftigung mit deren Eigenschaften (bedeutsam für die Kompetenzbereiche RuF, GuM, MSufZ).
					Allgemeine mathematische Vorerfahrungen (Beginn prozessbezogener Kompetenzen) Durch die Beobachtung anderer Menschen und im Dialog erfahren die Lernenden, dass die von ihnen gezeigten Handlungen gespiegelt und verbal begleitet werden. Die Nachahmungsfähigkeit wird so angebahnt und führt dazu, dass Gegenstände ihrer Funktion entsprechend genutzt werden. Eine unmittelbare Nachahmung ist damit noch nicht gesichert und entwickelt sich zunehmend.	Ich erlebe, dass es anderen Menschen wichtig ist, was ich tue, weil sie aufgreifen und nachmachen, was ich zeige. Ich schaue zu, wenn mir andere Menschen was vormachen und dazu sprechen. Das regt mich an, es nachzumachen.	Prozessbezogene Kompetenzen Bezugspersonen zeigen vorbildhaft die funktionsbezogene Nutzung von Gegenständen und regen zur Nachahmungsfähigkeit durch das Spiegeln gezeigter Handlungen an. Die sprachliche Begleitung unterstützt das Kommunizieren über konkret sichtbare Handlungen und Abläufe.
					Übergang zur elementaren Stufe: Vorzahlige Handlungen werden mit zahligem Handeln verbunden. Zahlwörter und Zahlen gewinnen im Alltag (zwei Äpfel, drei Brötchen), in Fingerspielen, Liedern und Geschichten und als Abbildungen sowie Mengenwissen (viel – wenig) an Bedeutung (bedeutsam für den Kompetenzbereich ZuO). Eigenschaften von Dingen werden verglichen (groß – klein, schwer – leicht, lang-kurz, kalt-heiß) (bedeutsam für den Kompetenzbereich GuM), räumliche und strukturierte Anordnungen (bedeutsam für den Kompetenzbereich MSufZ) dienen der Orientierung (oben-unten, hinten-vorne, aufgereiht, nebeneinander), die Gestalt der Dinge wird im Handeln erfahren (rund – eckig) (bedeutsam für den Kompetenzbereich RuF). Zeitliche Abläufe (erst – dann, gleich – später, Tage, Stunden, Minuten)) werden in sich wiederholenden Strukturen erfahren (bedeutsam auch für die Kompetenzbereiche GuM, DuZ, MSufZ)	Ich beginne, Zahlwörter und Zahlen im Alltag wahrzunehmen. Ich interessiere mich für Zahlen und Ziffern im Alltag, in Liedern und Geschichten. Ich handele mit Gegenständen in meiner Umgebung und beginne sie zu vergleichen und zu unterscheiden, ob sie groß oder klein, kurz oder lang, schwer oder leicht sind. Wenn ich mir eine Ansammlung von Gegenständen anschaue, kann ich einschätzen, ob es viel oder wenig Gegenstände sind. Ich kann sagen, wo sich die Dinge befinden (vorne, hinten…) und wie sie angeordnet sind (nebeneinander, übereinander usw.). Ich weiß, dass bestimmte Ereignisse jeden Tag, jede Woche zur gleichen Zeit stattfinden und kann darüber berichten. Ich habe eine Vorstellung dazu entwickelt, was es bedeutet, wenn ich einen Tag oder wenige Minuten auf etwas warten soll.	Inhalts- und prozessbezogene Kompetenzen Bezugspersonen thematisieren zahliges Handeln in Alltagszusammenhängen. Dabei werden die verschiedenen Bedeutungszusammenhänge bei der Verwendung von Zahlwörtern und Ziffern erklärt (Zahlen zum Abzählen, Zahlen zum Messen, Zahlen zum Bezeichnen (Haus-Nr., Auto-Nr.). Beispiele unter PIKAS Mathe ein Kinderspiel Literatur: (Koch u.a.2020) Die Lehrkraft beschreibt konkrete Handlungen im Alltag (bedeutsam für: GuM, DuZ, MSufZ) mit Mathematiksprache und regt zum Entdecken von mathematischen Handlungen an. Sie verwendet vorbildhaft Begriffe aus der Mathematiksprache (Darstellen, Kommunizieren): Zahlen, viel – wenig, mehr – wenige, um eins mehr, sind zusammen usw. Beispiele in: PIKAS: Fachwortschatz Mathematik
					Die Lernenden machen erste Erfahrungen mit dem Sammeln, Vergleichen und Dokumentieren von Daten. Die sich entwickelnde Fähigkeit des Zählens ermöglicht es ihnen zunehmend Daten zu sammeln und zu dokumentieren ( z.B. zur Anwesenheit, zu Wetterphänomen, genutze Transportmittel auf dem Weg zur Einrichtung, Autos auf dem Parkplatz zu bestimmten Zeiten, Farben der Kleidungsstücke, Lieblingsessen in der Lerngruppe usw.).	Ich interesse mich dafür, ob alle Lernenden meiner Gruppe an einem bestimmten Tag anwesend sind. Ich weiß, dass man die Anwesenheit in Listen eintragen kann. Ich interesse mich dafür, ob die Anwesenheit an verschiedenen Tagen gleich ist und inwiefern sie sich verändert. Ich weiß, dass ich diese Fragen gut beantworten kann, wenn die Anwesenheit in Listen eingetragen wurde, die mir den Vergleich ermöglichen. Ich interessiere mich dafür, wie sich z.B. das Wetter im Verlauf einer bestimmten Zeit verändert. Deshalb beobachte ich jeden Tag das Wetter und helfe beim Eintragen in der Übersicht, ob die Sonne scheint, Wolken zu sehen sind oder ob es regnet. Ich weiß, dass man heraus bekommen kann, was in unserer Gruppe häufig vorkommt und was selten ist (z.B. Lieblingsessen, Lieblingsfarben), wenn alle befragt werden und die Ergebnisse in Listen und Übersichten eingetragen werden.	Die Lernenden werden angeregt, Ereignisse in ihrem Alltag zielgerichtet zu beobachten und zu dokumentieren. Ausgangspunkt der Beobachtung sind Fragen wie: Wer ist heute anwesend? Welche Lieblingsgerichte gibt es in unserer Gruppe? Wie haben die einzelnen Lernenden heute die Einrichtung erreicht (mit dem Auto, zu Fuß, mit dem Rad…??). Anschließend werden die Daten in vorbereiteten Übersichten/ Listen dokumentiert. Dazu werden zunächst Abbildungen konkreter Objekte (Fotos) verwendet, bevor mit Strichlisten gearbeitet wird. Bsp. Wie haben die Lernenden heute die Einrichtung erreicht? Lernende sitzen im Kreis, berichten nacheinander und erhalten entsprechend ihrer Erzählung eine Fußgängerfigur, Spielzeugauto, -fahrrad, -bus usw. Die Objekte werden übersichtlich geordnet und vergleichend besprochen (kommuniziert). Die Lernenden werden angeleitet die Ergebnisse des Gesprächs in eine vorbereitete Tabelle/ Übersicht einzutragen (dargestellt). Abschließend werden die Ergebnisse erneut vergleichend diskutiert (argumentiert). Ministerium für Kultus BaWü Förderung mathematischer Kompetenzen in der Elementarbildung
					Zufall und Wahrscheinlichkeit: Die Lernenden beginnen zu verstehen, dass Ereignisse nicht immer auf der Basis des Ursache-Wirkung- Prinzips erklärbar sind, sondern dass diese sich auch zufällig ereignen können und deshalb nicht konkret/ sicher vorhersehbar sind. Zufall und die Wahrscheinlichkeit sind eng miteinander verbundene Begriffe, deren Bedeutung von den Lernenden ansatzweise verstanden wird. Die Lernenden gewinnen durch die Unterscheidung der Begriffe „sicher“, „wahrscheinlich“, „unmöglich“ erste Zugänge zum Phänomen der Wahrscheinlichkeit. Die komplexe mathematische Bedeutung ist im elementaren Bereich allerdings noch nicht zugänglich. Ministerium für Kultus BaWü Förderung mathematischer Kompetenzen in der Elementarbildung	Ich kann würfeln und das Würfebild (z.B. unterschiedliche Farben, Zahldarstellungen) erkennen. Ich weiß, dass ich vor dem Würfeln nicht sicher sagen kann, welches Würfelbild ich sehen werde. Ich weiß, dass das Würfelbild beim Würfeln (oder das Ergebnis beim Münzen werfen) durch meinen Wunsch (nicht beeinflusst wird und nicht vorhersehbar ist. Ich weiß also, dass die Ergebnisse bei diesen Handlungen zufällig sind. Ich denke darüber nach, was das Wort „wahrscheinlich“ bedeutet. Ich weiß, dass mit diesem Wort ausgedrückt wird, dass ein Ereignis eintreten könnte, aber nicht sicher eintreten muss. Wenn z.B. gesagt wird, dass es morgen wahrscheinlich regnen wird, dann sollte ich die Regenjacke mitnehmen. Es ist aber nicht sicher, dass es wirklich regnen wird. Ein Sonnentag ist auch nicht unmöglich.	Würfelspiele bieten vielfältige Möglichkeiten, um Gespräche über Zufall und Wahrscheinlichkeit anzuregen. Fragen, wie zum Beispiel die folgenden, initieren das Nachdenken und fordern zum Experimentieren auf: Wenn bei 5 Würfen keine 6 gewürfelt wurde, kommt dann beim 6. Wurf eher die 6? Kommen beim Würfeln bestimmte Zahlen häufiger vor als andere? Annäherungen zum Begriff der Wahrscheinlichkeit werden über Gesprächsangebote zur Vorhersagbarkeit von Ereignissen ermöglicht. Z.B. kann mit den Lernenden über die Aussage: „Wahrscheinlich regnet es morgen“ nachgedacht werden. Bedeutet die Aussage, dass es ganz bestimmt („sicher“) regnen wird? Ist das Wetterereignis „wahrscheinlich“, sind andere Wetterereignisse „unmöglich“? Eine weitere Frage dazu ist:: „Wenn es morgen wahrscheinlich regnet, regnet es dann sicher?“
					Die Lernenden machen zielgerichtet und selbstständig weitere Erfahrungen mit dem Sammeln von Daten und in der Verwendung von Darstellungsformen, die Vergleichsmöglichkeiten beinhalten (Anwesenheitslisten, Strichlisten (Fünferstruktur s. ZuO), Tabellen mit Piktogrammen zur Wetterbeobachtung usw.). Sie beteiligen sich an der Erstellung von Übersichten und Listen. Sie beobachten z.B. Wetterphänomene, nutzen dazu Messgeräte (Regenmessgeräte, Thermometer) und markieren auf einer Tabelle die jeweilige Menge usw. (bedeutsam auch für den Kompetenzbereich GuM). Lernende nutzen Wochenübersichten in Form von Tabellen mit Strichlisten (Beziehung zum Kompetenzbereich ZuO) für jeden Tag und klären Fragen, wie z.B. an welchem Tag die meisten Personen anwesend waren.	Ich kann Daten für Listen und Tabellen sammeln (z.B. Anwesenheit, Wetterereignisse, Nutzung bestimmter Arbeitsmittel/ Spielsachen) und die Daten selbstständig in Listen und Tabellen eintragen. Ich kann bei der Erstellung von Tabellen und Übersichten mitwirken. Ich weiß, dass es von Vorteil ist, wenn man Ereignisse in Form von Strichlisten dokumentiert. Ich kann bei Strichlisten Fünferbündel nutzen, damit sie übersichtlicher werden. Ich kann an der Wochen-Anwesenheitsliste erkennen, ob heute mehr oder weniger Personen als gestern da sind. Ich kann an der Regentabelle für diese Woche sehen, ob es am Montag mehr geregnet hat als am Mittwoch. Ich kann durch Abbildungen und Zählhilfen (Strichlisten, Perlenstäbe) sehen, welche Lieblingsfarbe am häufigsten in der Klasse gewählt wird oder welches Alter wie oft in der Klasse vorkommt usw.	Lehrkräfte integrieren vielfältig Tabellen und Listen zur Dokumentierung von alltäglichen Abläufen und Beobachtungen. Lernende werden angeregt, entsprechende Fragen zu stellen (kommunizieren), gemeinsam Darstellungsformen zu entwickeln, Daten systematisch zu sammeln, Dokumentationen anzufertigen, zu interpretieren und zu präsentieren (darstellen, argumentieren). PIKAS Wortspeicher Strichlisten zu unterschiedlichen Ereignissen und Situationen werden von den Lernenden geführt, Schaubilder werden gestaltet, Daten werden eingetragen, verglichen und interpretiert: häufig, selten usw.). Wetterphänomene werden mit Hilfe von Messgeräten (Regenmesser, Thermometer) gemessen, durch Symbole in Schaubildern abgebildet und verglichen (z.B. Regenmengen, Tagestemperaturen im Verlauf der Woche) (bedeutsam auch für den Kompetenzbereich GuM). Befragungen zu unterschiedlichen Inhalten werden durchgeführt (z.B. Lieblingsfarben, andere Bevorzugungen, Geschwister, Besitz von Spielzeug, Freizeitaktivitäten werden geplant, durchgeführt, dokumentiert. Die Ergebnisse werden visualisiert (Piktogramme, Tabellen, Perlenstäbe), präsentiert und diskutiert (dargestellt, argumentiert). s. Lerndokumentation Mathematik (S. 119 – 149) und Staatsinstitut MÜNCHEN (2008): Handreichung zu Daten, Häufigkeit und Wahrscheinlichkeit PIKAS Sammeln und Darstellen Lernaufgaben (IQ im Bildungswesen) PIKAS Lesen und Interpretieren
					Datenerhebung planen – Fragestellungen entwickeln Lernende entwickeln Fragestellungen, die sich aus ihrer Lebenswelt ergeben. Lernende sammeln durch Umfragen (Fragebögen) oder Beobachtungen (Strichlisten) Daten und notieren diese. Sie nutzen Wortspeicher: „Tabelle, Zeile, Spalte, Strichliste“. Lernende werten Daten aus und vergleichen diese miteinander. Sie ermitteln Anzahlen und setzen diese in Beziehung zueinander (z.B. in Ranglisten) (Beziehung zu ZuO). Die Ergebnisse und Informationen werden in Tabellen oder Diagrammen abgebildet. Aus Tabellen können Lernende Daten und Ergebnisse entnehmen und diese interpretieren. . Durch das strukturierte Vorgehen können Lernende Muster und Gesetzmäßigkeiten erkennen (Beziehung zum Kompetenzbereich MSufZ).	Ich interessiere mich für regelmäßige Abläufe und Besonderheiten in meinem Alltag und möchte diese genauer erkunden. Ich weiß, dass für jede Erkundung zuerst eine Frage formuliert werden muss. Ich kann meine Interessen in Form von Fragen zum Ausdruck bringen. Ich kann Fragestellungen beantworten, indem ich Erkundungen plane (Umfragen, gezielte Beobachtungen), diese vorbereite, durchführe und auswerte. Ich kann die Ergebnisse meiner Erkundungen in Tabellen oder Diagrammen sichtbar machen und die Daten so gut vergleichen. Ich kann die Ergebnisse meiner Erkundungen in Ranglisten ordnen und so erkennen und präsentieren, was am häufigsten, am zweithäufigsten usw. vorgekommen ist.
					Zufall und Wahrscheinlichkeiten Die Lernenden haben verstanden, dass Ereignisse sicher, möglich, unmöglich, wahrscheinlich oder zufällig zustande kommen können. Lernende lernen Chancen für das Eintreten von Ereignissen einzuschätzen und vergleichen sie durch datenbasierte Erkenntnisse. Lernende beschäftigen sich mit Zufällen und (Gewinn-)Wahrscheinlichkeiten z.B. bei Würfelspielen oder dem Glücksrad.	Ich weiß, was die Worte „wahrscheinlich“ und „Zufall“ bedeuten und wie sie zusammenhängen und verwende sie, wenn ich Handlungen beschreibe, deren Ergebnisse (z.B. Würfelspiele, Kartenspiele, Glücksrad) nicht sicher vorhergesagt werden können. Z. B.: Welches Würfelbild nach dem Würfeln zu sehen sein wird, ist nicht vorhersehbar und deshalb zufällig. Die Wahrscheinlichkeit, welche Zahl es sein wird, ist für alle Zahlen gleich groß.	Lernangebote für Zufall und Wahrscheinlichkeiten PIKAS Wahrscheinlichkeiten Zufallsexperimente PRIMAKOM Zufall und Wahrscheinlichkeit
					Kombinieren Lernende erkunden beim Kombinieren die Anzahl möglicher Anordnungen (bedeutsam auch für die Kompetenzbereiche ZuO, RuF). Ausgehend vom intuitiven (unsystematischen) Ausprobieren werden systematische Herangehensweisen kennen. Zentrale Unterrichstziele s. PIKAS Daten Häufigkeiten und Wahrscheinlichkeiten	Wenn mir unterschiedliche gefärbte oder geformte Steine zum Turmbauen zur Verfügung stehen, weiß ich, dass unterschiedlich aussehende Türme entstehen können. Ich probiere systematisch alle Möglichkeiten aus die Steine zu stapeln und kann dann sagen, wie viele Varianten von Türmen es insgesamt gibt.	Lernangebote zum Kombinieren: Lernaufgaben (IQ im Bildungswesen) PRIMAKOM Hintergrund Kombinatorik Beispiel PIKAS Würfeltürme
					Prozessbezogene Kompetenzen Lernende kommunizieren über Fragestellungen, die sie durch Befragungen von Menschen oder Beobachtung von Phänomenen bearbeiten, lösen und darstellen können. „Was wollen wir herausfinden oder beobachten? Wie muss die Frage lauten? Was können wir in welcher Weise beobachten? Wie können wir die Ergebnisse abbilden usw.?“ Sie bilden ihre Ergebnisse ab und erklären die Erstellung und Dokumentation (Darstellen, Argumentieren, Vergleichen). Sie kommunizieren über die relevanten Informationen aus den Darstellungen	Ich rede mit Anderen über geplante Beobachtungen und Befragungen. Wir beraten dann gemeinsam, wie die Fragestellung lautet, wie wir vorgehen könnten und wie wir die Arbeit aufteilen werden. Wir denken gemeinsam darüber nach in welcher Form wir die Daten sammeln und wie wir sie erfassen und darstellen können. Wir besprechen die Ergebnisse unserer Erkundungen, vergleichen die Daten und überlegen, wie wir sie präsentieren und wie wie wir unsere Schlussfolgerungen begründen können.	Prozessbezogene Kompetenzen Zur Problemlösung werden Lernende angeregt, systematisches Probieren in Tabellen usw. darzustellen. Ein Wortspeicher zum Bereich Daten und Zufall ermöglicht, die Fragestellung zu kommunizieren, Lösungswege und Ergebnisse zu interpretieren und zu vergleichen. Lehrkräfte bieten dazu Mathekonferenzen als Format an. PIKAS Mathekonferenz
					Daten erheben, Erhebungen planen Lernende planen Datenerhebungen zu bestimmten Fragestellungen und führen sie durch, erheben Daten und fassen sie in Ur- und Strichlisten zusamme, nutzen zur Erfassung von Daten auch eine Tabellenkalkulation, planen statistische Erhebungen, auch unter den Aspekten Stichprobenauswahl und Erhebungsinstrument.	Ich kann Datenerhebungen zu einer bestimmten Fragestellung planen und durchführen. Ich kann Daten sammeln, indem ich Strichlisten erstelle, die Häufigkeiten auszähle und in Tabellen zusammenfasse. Ich kann Tabellenkalkulationen bei der Erfassung von Daten nutzen. Ich überlege mir bei der Planung von Erhebungen, woraus meine Stichprobe bestehen soll (z.B. Lernende meiner Klasse, vorbeifahrende Autos) und wie groß sie sein soll. Ich wähle ein passendes Erhebungsinstrument aus (z.B. Fragebogen, Beobachtungsbogen).	Ziel ist das Durchlaufen der Phasen einer statistischen Untersuchung: Problem – Plan – Datenerhebung – Analyse – Zusammenfassung. Bevor die Lernenden eine Erhebung planen, sollten sie Daten selbständig erfasst haben und ausgewertet haben. So wird das Planen vorbereitet. Fragestellungen sollten für die Lernenden relevant/interessant sein und aus ihrem Erfahrungsbereich stammen. Zuerst Erhebungen in der eigenen Klasse durchführen, bevor Stichproben erweitert werden.
					Daten darstellen Lernende stellen Häufigkeitstabellen zusammen und veranschaulichen diese mit Hilfe von Säulen- und Kreisdiagrammen, erstellen von Diagrammen, auch mit Hilfe digitaler Mathematikwerkzeuge, nutzen Median, Spannweite und Quartile zur Darstellung von Häufigkeitsverteilungen als Boxplots, können Boxplots erstellen und interpretieren, können Datensätze mit Hilfe von Boxplots vergleichen.	Ich kann Häufigkeitstabellen erstellen und Anzahlen in einem Säulen- oder Balkendiagramm darstellen. Ich kann zu einem Datensatz verschiedene Diagramme (Säulen-, Balken-, Linien- und Kreisdiagramm), auch mit digitalen Mathematikwerkzeugen, erzeugen. Ich kann (mit digitalen Mathematikwerkzeugen) Daten interpretieren, indem ich Median, Minimum, Maximum, Spannweite, Quartile berechne und Boxplots erstelle. Ich kann einen Boxplot erstellen und interpretieren. Ich kann Datensätze mit Hilfe von Boxplots vergleichen.	Digitale Mathematikwerkzeuge: - CODAP - Excel Um Kreis- und Banddiagramme zu erstellen, sind Kenntnisse der Bruch- und Prozentrechnung notwendig. In Häufigkeitstabellen können absolute und relative Häufigkeiten (Bruch und Prozent) eingetragen werden. So werden Zusammenhänge deutlich und auch, dass die Summe der relativen Häufigkeiten 1 ergibt. Mit Datenkarten, z.B. Klebezettel mit Geburtstag der Lernenden, können Säulendiagramme erarbeitet werden. Sie werden geordnet, z.B. alle Karten der Geburtstage im Mai werden übereinander geklebt, anschließend wird die Verteilung auf Kästchenpapier übertragen .
					Daten auswerten Lernende lesen statistische Darstellungen. Sie entnehmen einfache Informationen aus der grafischen Darstellung, ohne das Zusammenhänge beachtet werden müssen („reading the data“), z.B. absolute Häufigkeiten, können das arithmetische Mittel und Median zu gegebenen Daten bestimmen und erklären, was sie in Bezug auf die Daten bedeuten, können erklären, was arithmetisches Mittel und Median bedeuten und was der Unterschied zwischen diesen beiden Mittelwerten ist, lesen und interpretieren von Daten. Sie finden Zusammenhänge und Beziehungen zwischen den einzelnen Daten. Dafür setzen sie Daten miteinander in Beziehungen, z.B. Minimum, Maximum, Spannweite und Quartile („reading between the data“).	Ich kann Informationen aus Diagrammen ablesen (Häufigkeiten). Ich kann das arithmetische Mittel/den Durchschnitt und Median/Zentralwert zu gegebenen Daten bestimmen und erklären, was sie in Bezug auf die Daten bedeuten. Ich kann erklären, was arithmetisches Mittel und Median bedeuten und was der Unterschied zwischen diesen beiden Mittelwerten ist. Ich kann Zusammenhänge zwischen den Daten erkennen, z.B. indem ich mir Minimum, Maximum, Spannweite und Quartile anschaue und überlege, was sie bedeuten.	Es gibt verschiedene Grundvorstellungen zum arithmetischen Mittel, die im Unterricht thematisiert werden sollen, damit es nicht nur eine Formel ist: Durchschnitt Ausgleichswert Schwerpunkt
					Daten reflektieren Lernende hinterfragen Daten („reading byond the data“), analysieren grafische statistische Darstellungen kritisch und erkennen Manipulationen, können gewählte Darstellungsform von Diagrammen begründen, reflektieren mit Hilfe der mathematischen Kenntnisse den Umgang mit und die Darstellung von Daten in Medien, etwa in Bezug auf die Absicht und mögliche Wirkungen der Darstellung.	Ich kann Daten hinterfragen, indem ich überleg, wie sie zustande gekommen sind und wodurch sie beeinflusst sein könnten. Ich kann grafische statistische Darstellungen kritisch analysieren und Manipulationen erkennen. Ich kann gewählte Darstellungsformen von Diagrammen begründen. Ich kann Diagramme hinsichtlich ihrer Wirkung kritisch beurteilen.	Checkliste zum Prüfen statistischer Informationen erarbeiten, siehe z.B. Krüger et al., 2015, S. 152
					Ergebnis und Ereignis bei Zufallsexperimenten Lernende unterscheiden zwischen Ergebnis und Ereignis. Sie nennen alle möglichen Ergebnisse eines Zufallsexperiment (Ergebnismenge). Sie beschreiben Ereignisse, die sich aus mehreren Ergebnissen zusammensetzen können.	Ich kenne den Unterschied zwischen Ergebnis und Ereignis bei Zufallsexperimenten. Ich kann bei einem Zufallsexperiment alle möglichen Ergebnisse nennen. Ich kann mögliche Ereignisse beschreiben, z.B. ungerade Augenzahl beim Würfeln.	Zuerst alle möglichen Ergebnisse notieren und dann über bestimmte Ereignisse sprechen. Ein Ereignis kann sich aus mehreren Ergebnissen zusammensetzen.
					Zugänge zur Wahrscheinlichkeit Lernende benutzen relative Häufigkeiten von langen Versuchsreihen zur Schätzung von Wahrscheinlichkeiten (empirisch frequentistischer Zugang). Dafür berechnen die Lernenden relative Häufigkeiten, erkennen, dass beim empirisch frequentistischen Zugang die Schätzungen besser werden, je mehr Daten vorliegen (empirisches Gesetz der großen Zahlen), bestimmen Wahrscheinlichkeiten bei einstufigen Zufallsexperimenten mit Hilfe der Laplace-Regel. Dafür setzen sie die günstigen Fälle ins Verhältnis zu allen möglichen Fällen (theoretischer Zugang), können entscheiden, ob sie die Wahrscheinlichkeit eines Zufallsgeräts besser theoretisch durch Überlegen oder empirisch durch Probieren bestimmen, geben Wahrscheinlichkeiten quantitativ an als Werte zwischen 0 und 1, als Bruch oder als Prozentangabe.	Ich kann absolute Häufigkeiten in relative Häufigkeiten umrechnen, um zu vergleichen. Ich kann die Wahrscheinlichkeit von Zufallsgeräten vergleichen, indem ich häufig genug werfe und so eine Näherung für die Wahrscheinlichkeit praktisch bestimmen. Ich kann erklären, warum ich bei großen Wurfzahlen die Wahrscheinlichkeit besser angeben kann. Ich kann bei Zufallsgeräten entscheiden, ob man mit ihnen einen Laplace-Versuch durchführen kann, und in solchen Fällen die Wahrscheinlichkeit allein durch Überlegen bestimmen. Ich kann bei Zufallsgeräten entscheiden, ob ich die Wahrscheinlichkeiten besser theoretisch durch Überlegen oder praktisch durch Probieren bestimme. Ich kann Wahrscheinlichkeiten mit einer Zahl angeben.	Für Zufallsexperimente, die einen frequentistischen Zugang bieten, sind neben dem klassischen Würfel Riemer-Quader oder Schweine-Würfel geeignet. Für Simulationen hoher Wurfzahlen sind im Internet Würfelsimulatoren zur finden.
					Einstufige Zufallsexperimente und Modellierungskreislauf Lernende erkennen Zufallsereignisse im Alltag und modellieren sie: o beschreiben eine reale stochastische Situation und entwickeln eine Fragestellung, o treffen Modellannahmen und visualisieren sie (z.B. mit Baumdiagramm), o berechnen Wahrscheinlichkeit, o prüfen, ob Daten aus einem realen Experiment mit dem theoretischen Modell des Zufallsexperiment kompatibel sind. Lernende nutzen Simulationen, um stochastische Fragen zu entscheiden.	Ich kann Zufallsereignisse im Alltag erkennen. Ich kann Zufallsereignisse beschreiben und Fragen zur Wahrscheinlichkeit stellen. Ich kann zur Beantwortung der Fragen Baumdiagramme oder andere Skizzen erstellen. Ich kann prüfen, ob die Ergebnisse des Experiment mit den theoretischen Annahmen übereinstimmen. Ich kann Zufallsprozesse durch Simulationen beschreiben.	Erläuterungen zum Modellierungskreislauf: Krüger et al., 2025, S. 13
					Mehrstufige Zufallsexperimente Lernende veranschaulichen zweistufige Zufallsexperimente mit Hilfe von Baumdiagrammen, bestimmen Wahrscheinlichkeiten bei zweistufigen Zufallsexperimenten mit Hilfe der Pfadregeln, o wenden die Pfadmultiplikationsregel an. o wenden die Pfadadditionsregel an. Lernende veranschaulichen mehrstufige Zufallsexperimente mit Hilfe von Baumdiagrammen, können die Wahrscheinlichkeiten in mehrstufige Zufallsexperimenten rechnerisch bestimmen, interpretieren Wahrscheinlichkeitsaussagen.	Ich kann bei Zufallsexperimenten mit zwei Schritten mit einem Baumdiagramm darstellen. Ich kann bei Zufallsexperimenten mit zwei Schritten die Wahrscheinlichkeiten mit Hilfe der Pfadregeln berechnen. Ich kann die Pfadmultiplikationsregel anwenden, wenn ich die Wahrscheinlichkeit eines zusammengesetzten Ergebnisses berechne. Ich kann die Pfadadditionsregel anwenden, um die Wahrscheinlichkeit eines Ereignisses zu berechnen, das aus mehreren Ergebnissen besteht. Ich kann mehrstufige Zufallsversuche als Baumdiagramm darstellen. Ich kann Wahrscheinlichkeiten in mehrstufigen Zufallsversuchen rechnerisch bestimmen. Ich kann sagen, was die Wahrscheinlichkeiten für den Alltag bedeuten.	Um die Struktur eines mehrstufigen Vorgangs in einem Baumdiagramm darzustellen, kann es hilfreich sein, eine Schrittfolge zu erarbeiten. Dafür wird eine zeitliche Abfolge durchlaufen: Was kann zuerst passieren? Welche Möglichkeiten bestehen dann? Baumdiagramme können von oben nach unten oder von links nach rechts gezeichnet werden. Evtl. zuerst das Erstellen von Baumdiagrammen ohne Wahrscheinlichkeitsangaben üben.
					Bedingte Wahrscheinlichkeit Lernende erkennen Aufgaben, in denen bedingte Wahrscheinlichkeiten berechnet werden sollen, können zur Berechnung bedingter Wahrscheinlichkeiten ein Baumdiagramm zeichnen, können bedingte Wahrscheinlichkeiten mit Hilfe der Vierfeldertafel darstellen und berechnen.	Ich kann Aufgaben erkennen, in denen bedingte Wahrscheinlichkeiten berechnet werden sollen. Ich kann zur Berechnung bedingter Wahrscheinlichkeiten ein Baumdiagramm zeichnen. Ich kann bedingte Wahrscheinlichkeiten mit Hilfe der Vierfeldertafel darstellen und berechnen.	Folgende Teilschritte können den Lernprozess unterstützen: Teil-Ganzes-Beziehungen beschreiben und erklären Unterschiede zwischen Anteilen an unterschiedlichem Ganzen beschreiben und erklären Wahrscheinlichkeiten beschreiben: Unter der Bedingung, dass … Weitere Hinweise und Ideen: https://sima.dzlm.de/unterricht/unterrichtsmaterialien-sekundarstufe

Zum Inhaltsverzeichnis zurück

Tabelle 3.5: Strukturen und funktionaler Zusammenhang

Abkürzungen Tabellen: b = basal | e = elementar | p = primär | s = sekundär


					Teilbereich: Strukturen und Funktionaler Zusammenhang
b	e	p	s	ILZ	Stufe in Erwachsenensprache	Stufe in Kindersprache	Lernbausteine
					Die Lernziele des Teilbereichs: „Strukturen und Funktionaler Zusammenhang“ werden im Bezug auf basale, elementare und primare Zugänge inhaltsübergreifend bearbeitet und sind deshalb eingebunden in die Stufenmodelle der Teilbereiche: „Zahl und Operationen“, „Größen und Messen“, „Raum und Form“ sowie „Daten und Zufall“.
			x		Zusammenhänge erkennen, darstellen und beschreiben Die Lernenden stellen Beziehungen zwischen Zahlen und zwischen Größen in Tabellen und Diagrammen dar, lesen Informationen aus Tabellen und Diagrammen in einfachen Sachzusammenhängen ab, erkunden Muster in Beziehungen zwischen Zahlen und stellen Vermutungen auf, stellen Zuordnungen mit eigenen Worten, in Wertetabellen, als Grafen und in Termen dar und wechseln zwischen diesen Darstellungen.	Ich kann einfache Zusammenhänge zwischen Zahlen und Größen in einer Tabelle darstellen. Ich kann passende Diagramme (z B. Balkendiagramme) erstellen, um Zusammenhänge zwischen Zahlen und Größen darzustellen. Ich kann Informationen aus Tabellen und Diagrammen ablesen und in eigenen Worten erklären. Ich kann Muster in Zahlenfolgen oder Rechenregeln erkennen und Vermutungen darüber aufstellen. Ich kann eine Zuordnung mit eigenen Worten beschreiben. Ich kann Wertepaare in einer Tabelle darstellen. Ich kann eine Zuordnung als Graph im Koordinatensystem zeichnen. Ich kann einen Term oder eine Funktionsgleichung für eine Zuordnung aufstellen. Ich kann in der Argumentation zwischen Text, Tabelle, Graph und Term hin- und herwechseln, um eine Situation zu beschreiben.	Auf der Seite von „Mathe sicher können“ sind Materialien zur Proportionalität, die genutzt werden können: https://mathe-sicher-koennen.dzlm.de/material-sek/sachrechnen Figurierte Zahlen eignen sich um Muster und Zusammenhänge zu beschreiben: https://adi.dzlm.de/figurierte-zahlen
			x		Rechnen mit Variablen Die Lernenden verwenden Variablen je nach Kontext als eine feste Zahl, als eine beliebige Zahl aus einem Zahlenbereich und als Veränderliche in einem bestimmten Bereich und können Beispiele für die unterschiedliche Verwendung von Variablen nennen. Teilziele Die Lernenden erkennen und verwenden Variablen als Platzhalter für eine feste, aber noch unbekannte Zahl, verstehen Variablen als allgemeine, beliebige Zahl innerhalb eines Zahlenbereichs und verwenden sie zur Beschreibung mathematischer Strukturen oder Rechengesetze, erkennen Variablen als veränderliche Größen im funktionalen Zusammenhang und nutzen sie zur Darstellung von Beziehungen zwischen Größen.	Ich kann Variablen je nach Situation als feste Zahl, als beliebige Zahl oder als veränderliche Größe verstehen und Beispiele dafür nennen Ich kann eine Variable als Platzhalter für eine noch unbekannte Zahl verwenden und in einem Sachkontext erklären, was sie bedeutet. Ich kann eine Variable als allgemeine, beliebige Zahl in einem Zahlenbereich verstehen und damit mathematische Strukturen oder Rechengesetze beschreiben. Ich kann mit einer Variable Beziehungen zwischen Größen darstellen, z.B. kann ich beim Flächeninhalt sagen, wie sich a verändert, wenn sich b verdoppelt und die Fläche unverändert bleibt.	Auf dieser Seite sind Unterrichtsmaterialien und Diagnoseaufgaben zum ersten Umgang mit Variablen: https://maco.dzlm.de/verstehensgrundlagen-zu-variablen-termen-gleichungen
					Terme Terme als Rechenaufforderung Die Lernenden erkennen Terme als Rechenaufforderung und führen entsprechende Berechnungen korrekt durch, wenden Rechenregeln (z.B. Punkt-vor-Strich) sicher auf Terme an. Terme als Objekt Die Lernenden vergleichen Terme hinsichtlich ihrer Struktur und erkennen, ob zwei Terme äquivalent sind, interpretieren Terme als Beschreibung von Zusammenhängen in mathematischen oder realen Situationen. Mit Termen Situationen beschreiben (Modellieren) Die Lernenden identifizieren relevante Größen in Sachsituationen und stellen passende Terme auf, nutzen Terme zur Beschreibung von Sachsituationen im Rahmen des Modellierungskreislaufs, überprüfen, ob ein aufgestellter Term zur beschriebenen Situation passt. Terme aufstellen Die Lernenden formulieren zu Sachsituationen, Punkt- und Zahlenmustern mathemische Terme, übersetzen sprachliche oder grafische Darstellungen (z B. Tabellen, Skizzen) in Terme. Terme umformen (kalkülmäßiger Umgang) Die Lernenden wenden Umformungsregeln sicher an (z. B. Ausmultiplizieren, Ausklammern, Zusammenfassen von Termen), zeigen, dass zwei Terme gleichwertig sind, indem sie sie zielgerichtet umformen, begründen Umformungsschritte unter Verwendung mathematischer Fachsprache, können unbekannte Zahlen finden, für die ein Term einen bestimmten Wert annimmt, können in Termen die Zahlen verändern und Auswirkungen auf den Wert des Terms untersuchen.	Ich verstehe Terme als Rechenaufforderung und kann entsprechende Rechnungen durchführen. Ich wende Rechenregeln sicher auf Terme an. Ich kann Term vergleichen und erkennen, ob zwei Terme gleich sind. Ich interpretiere Terme als Beschreibung von Zusammenhängen in mathematischen und realen Situationen. Ich erkenne in Sachsituationen relevante Größen zum Aufstellen eines Terms. Ich kann Terme zur Beschreibung von Sachsituationen nutzen und löse sie mathematisch. Ich kann prüfen, ob die Lösung zur Sachsituation passt. Ich kann zu Sachsituationen, Punkt- und Zahlenmustern mathematische Terme aufstellen. Ich kann zu einer Situation mit veränderbaren Zahlen einen Term mit Variablen aufschreiben. Ich kann sprachlich oder tabellarisch dargestellten Situationen und Mustern Terme aufstellen. Ich kann Terme umformen und dabei Rechenregeln sicher anwenden, z.B. Ausklammern. Ich kann durch Umformen zeigen, dass zwei Terme gleichwertig sind. Ich kann Umformungsschritte beschreiben und begründen. Ich kann unbekannte Zahlen finden, für die ein Term einen bestimmten Wert annimmt. Ich kann in Termen die Zahlen verändern und Auswirkungen auf den Wert des Terms untersuchen.	Für den Umgang mit Termen sind die Sichtweisen „Terme als Aufforderung zum rechnerischen Operieren“ und „Term als Objekt“ wesentlich. Steht ein Term in Beziehung zu einem anderen Term, wird er vor allem als Objekt betrachtet (vgl. Barzel et al., 2021, S. 11). Strategien zum Verstehen von Termstrukturen können entwickelt werden. Auch bei Termen sind der Darstellungswechsel und die Verknüpfung der verschiedenen Darstellungsebenen zentral: Formal-symbolisch: Term mit Variablen - Numerisch-tabellarisch: Zahlenterm (konkrete Gleichung) Situativ-sprachlich: verbale Beschreibung der Situation Graphisch-visuell: Bild Das Aufstellen von Termen zu Bilderfolgen/Situationen ist eine wichtige Grundlage, Variablen und Terme in ihrer Bedeutung zu erfassen.
					Gleichungen Deutung des Gleichheitszeichens Gleichung als Relation Die Lernenden deuten das Gleichheitszeichen als Ausdruck einer Gleichheit zweier Terme (nicht als Rechenaufforderung) und erkennen, dass beide Seiten einer Gleichung denselben Wert beschreiben. Gleichungen aufstellen Die Lernenden nutzen Tabellen, grafische Darstellungen oder Textinformationen zur Formulierung einfacher Gleichungen, übersetzen Sachsituationen in passende Gleichungen, indem sie Beziehungen zwischen Größen mathematisch ausdrücken. Gleichungen lösen informeller Zugang und erste Strategien Die Lernenden bestimmen unbekannte Größen durch Probieren, logisches Argumentieren oder systematisches Vorgehen. nutzen Tabellen, Skizzen oder grafische Darstellungen (z B. Zuordnungspunkte) zur Bestimmung unbekannter Werte. überprüfen gefundene Werte durch Einsetzen in die Gleichung. Gleichungen lösen – modellgestützte Verfahren Die Lernenden nutzen Modelle wie das Waagenmodell oder Rückwärtsrechnen, um Gleichungen zu lösen, erkennen, dass durch gleichartige Operationen auf beiden Seiten der Gleichung die Lösungsmenge erhalten bleibt. Gleichungen lösen –formale Verfahren Die Lernenden wenden Äquivalenzumformungen an, um lineare Gleichungen zu lösen, begründen ihre Umformungsschritte durch Rückgriff auf das Modell oder mathematische Regeln, lösen Gleichungen rechnerisch, auch wenn die Lösung nicht mehr anschaulich modelliert werden kann.	Ich weiß, dass auf beiden Seiten vom Gleichheitszeichen der gleiche Wert ausgedrückt wird. Ich kann zu den Werten in einer Tabelle eine Gleichung aufstellen. Ich kann zu Sachsituationen Gleichungen aufstellen. Ich kann unbekannte Größen in Gleichungen herausfinden, indem ich (systematisch) ausprobiere oder nachdenke. Ich kann Tabellen oder Skizzen erstellen, um unbekannte Werte herauszufinden. Ich kann gefundenen Werte überprüfen, indem ich sie in die Gleichung einsetze. Ich kann Gleichungen lösen und stelle mir dabei das Waagenmodell vor oder rechne rückwärts. Ich kann beschreiben, dass bei Gleichungen die Lösungsmenge gleich bleibt, wenn ich auf beiden Seiten das Gleiche mache. Ich kann lineare Gleichungen durch Umformen lösen. Ich kann Umformungsschritte begründen. Dabei beziehe ich mich auf mathematische Regeln. Ich kann Gleichungen rechnerisch lösen.	Unterrichtskonzepte zum ersten Umgang mit Gleichungen, 3 Stufen: Anregung von informellen Wegen, also z. B. durch probierendes und argumentierendes Bestimmen von unbekannten Größen in Sachsituationen oder Ablesen von Eingabewerten von Graphen Anbieten von Modellen mit Handlungen, die eine Entwicklung der Äquivalenzumformungen ermöglichen (z. B. Waagemodell, Rückwärtsrechnen) Abstraktion und Ausweitung des modellhaften Lösens auf allgemeine, zum Teil im Modell nicht mehr durchführbare Äquivalenzumformungen Waagenmodell: tragfähiges Modell, um das äquivalente Umformen von Gleichungen zu verstehen Modell Nutzen der Elementaroperationen: Umkehraufgaben werden genutzt; sie verdeutlichen, warum man eine bestimmte Umformung zur Lösung nutzt
					Funktionen allgemein Die Lernenden erkennen Funktionen als eindeutige Zuordnungen zwischen zwei Größen, unterscheiden Funktionen von nicht-funktionalen Zuordnungen (z B. durch Prüfung auf Eindeutigkeit), stellen Funktionen in verschiedenen Darstellungsformen dar (z. B. Wertetabelle, Graph, situativ-sprachlich, Gleichung), - lesen Informationen aus verschiedenen Darstellungsformen von Funktionen heraus, wechseln zwischen Wertetabellen, Graphen, Funktionsgleichungen und situativen-sprachlichen Darstellungsformen. Die Lernenden verfügen über verschiedene Grundvorstellungen zu Funktionen: o die Zuordnungsvorstellung: verstehen, dass einer unabhängigen Variable genau ein Funktionswert zugeordnet wird. o die Kovariationsvorstellung: beschreiben, wie sich die Funktionswerte ändern, wenn sich die Eingabewerte verändern und erkennen und beschreiben Zusammenhänge wie „je mehr – desto…“ oder „wenn x wächst, dann…“. o die Objektvorstellung: beschreiben Funktionen als ganzheitliche Objekte (z. B. als Kurve im Koordinatensystem). Eigenschaften von Funktionen Die Lernenden erkennen und benennen einfache Eigenschaften von Funktionen, z. B. Nullstellen, Symmetrie, Stetigkeit, Monotonie.	Ich kann beschreiben, dass Funktionen eindeutige Zuordnungen von zwei Größen sind. Ich kann sagen, ob es sich um eine Funktion oder nicht-funktionale Zuordnungen handelt. Ich kann Funktionen unterschiedlich darstellen: mit Wertetabellen, als Graph, als Beschreibung und als Gleichung. Ich kann den Darstellungen Informationen entnehmen. Ich kann zwischen den Darstellungsformen (Wertetabellen, Graph, Beschreibung, Gleichung) wechseln. Ich kann an einem Beispiel erklären, dass bei einer Funktion einer Variablen ein Funktionswert zugeordnet wird. Ich kann beschreiben, wie sich die Funktionswerte ändern, wenn sich der Eingabewert ändert. ch kann beschreiben, wie der Graph einer Funktion aussieht.	Auf dieser Seite sind Ideen, wie funktionale Zusammenhänge sprachsensibel eingeführt werden können: https://sima.dzlm.de/unterricht/unterrichtsmaterialien-sekundarstufe
					Proportionale Zusammenhänge Die Lernenden identifizieren proportionale, antiproportionale und lineare Zuordnungen in Tabellen, Termen und Realsituationen, beschreiben, wie sich proportionale, antiproportionale und lineare Zuordnungen verhalten, entscheiden, ob ein gegebener Zusammenhang proportional is z B. durch Überprüfung der Verhältnisse in einer Tabelle, ergänzen fehlende Werte in Tabellen proportionaler Zuordnungen korrekt, erklären, was eine Tabelle, ein Graph oder ein Term über eine Situation aussagt, können Ergebnisse in eigenen Worten deuten, können Aufgaben mit linearen, proportionalen oder antiproportionalen Zuordnungen selbstständig lösen, können dabei auch digitale Hilfsmittel (z. B. Tabellenkalkulation, Funktionsplotter) einsetzen.	Ich kann proportionale, antiproportionale und lineare Zuordnungen in Tabellen, Termen und Alltagssituationen erkennen. Ich kann beschreiben, wie sich proportionale, antiproportionale und lineare Zuordnungen verhalten. Ich kann entscheiden, ob ein Zusammenhang proportional ist – zum Beispiel, indem ich die Zahlen in einer Tabelle vergleiche. Ich kann fehlende Werte in einer Tabelle mit proportionaler Zuordnung richtig ergänzen. Ich kann erklären, was eine Tabelle, ein Graph oder ein Term über eine Situation aussagt. ch kann meine Ergebnisse in eigenen Worten erklären und sie auf die Situation beziehen. Ich kann Aufgaben mit proportionalen, antiproportionalen oder linearen Zuordnungen selbstständig lösen. Ich kann digitale Hilfsmittel nutzen, wie zum Beispiel Tabellenkalkulation oder einen Funktionsplotter, um solche Aufgaben zu bearbeiten.	Auf dieser Seite sind Ideen, wie proportionale und antiproportionale Zusammenhänge sprachsensibel eingeführt werden können: https://sima.dzlm.de/sites/simams/files/uploads/sima-sprachanfang_proportional_antiproportional-200518.pdf
					Lineare Funktionen und Gleichungen Die Lernenden erkennen lineare, proportionale und antiproportionale Zuordnungen in Tabellen, Graphen, Gleichungen und Realsituationen und unterscheiden sie voneinander, stellen Tabellen, Graphen und Gleichungen zu linearen Funktionen auf und nutzen sie zur Bestimmung weiterer Werte, beschreiben die Merkmale linearer Funktionen, insbesondere konstante Änderungsrate (Steigung) und Startwert (y-Achsenabschnitt), in verschiedenen Darstellungen, deuten die Parameter in der Funktionsgleichung einer linearen Funktion in Bezug auf ihren Einfluss auf den Graphen und den realen Zusammenhang, wenden lineare Funktionen zur Bearbeitung realitätsnaher Probleme an, auch unter Verwendung digitaler Werkzeuge, bestimmen Schnittpunkte zweier linearer Funktionen näherungsweise, z B. durch Ablesen an Tabellen oder Graphen. stellen zu Sachsituationen passende lineare Gleichungen auf, in denen eine unbekannte Größe gesucht ist, lösen lineare Gleichungen mit verschiedenen Verfahren (Probieren, Rückwärtsrechnen, Äquivalenzumformung) und bewerten deren Effizienz, nutzen digitale Werkzeuge (z. B. Tabellenkalkulation, Funktionsplotter) zur Darstellung und Lösung linearer Funktionen und Gleichungen.	Ich kann erkennen, ob eine Zuordnung proportional, antiproportional oder linear ist zum Beispiel in einer Tabelle, einem Graphen, einer Gleichung oder einer Alltagssituation. Ich kann zu einer linearen Funktion eine Tabelle, einen Graphen oder eine Gleichung aufstellen und damit weitere Werte berechnen. Ich kann beschreiben, was bei einer linearen Funktion immer gleich bleibt (z B. wie stark der Wert wächst oder sinkt) und wie der Startwert aussieht. ch kann erklären, was die Zahlen in einer Funktionsgleichung bedeuten (z. B. die Steigung oder der Anfangswert) und wie sie den Graphen verändern. Ich kann Aufgaben mit linearen Funktionen lösen, bei denen ich zum Beispiel ein Problem aus dem Alltag rechnerisch oder mit einer Darstellung bearbeiten muss. Ich kann erkennen, wo sich zwei lineare Funktionen schneiden zum Beispiel, indem ich in einer Tabelle oder in einem Graphen die gleichen Werte finde. Ich kann zu einer Situation eine passende lineare Gleichung aufstellen, wenn eine Größe unbekannt ist und ich sie berechnen möchte. Ich kann einfache lineare Gleichungen auf verschiedene Arten lösen zum Beispiel durch Probieren, Rückwärtsrechnen oder schrittweises Umformen. Ich kann digitale Hilfsmittel wie einen Funktionsplotter oder eine Tabellenkalkulation verwenden, um lineare Funktionen darzustellen oder Gleichungen zu lösen.	Auf diesen Seiten sind Ideen, wie lineare Funktionen und Gleichungen sprachsensibel eingeführt werden können und Diagnose- und Fördermaterial stehen zur Verfügung: https://maco.dzlm.de/verstehensgrundlagen-zu-funktionen https://maco.dzlm.de/sites/maco/files/material-lul/dzlm_difsek_funktionen_regelschul_lineare_fkt_240117.pdf
					Quadratische Funktionen Die Lernenden können quadratische Funktionen in Tabellen, Graphen und Termen darstellen und passende Werte berechnen, beschreiben die Form und Eigenschaften des Graphen einer quadratischen Funktion (Parabel) und erklären, wie sich der Graph bei Veränderung der Parameter verändert, erkennen den Scheitelpunkt und die Achsensymmetrie einer Parabel und erklären ihre Bedeutung im Sachzusammenhang, bestimmen die Nullstellen einer Parabel grafisch oder rechnerisch und interpretieren sie im Kontext, erklären, wann eine quadratische Gleichung zwei, eine oder keine Lösung hat, und veranschaulichen dies an Beispielen, lösen quadratische Gleichungen durch Ablesen am Graphen oder durch Rückwärtsrechnen, insbesondere bei Termen in Scheitelpunktform, lösen quadratische Gleichungen rechnerisch und wählen dazu passende Verfahren, z B. mithilfe der binomischen Formeln oder durch Umformen, stellen zu Sachsituationen passende quadratische Gleichungen auf, wenn eine gesuchte Größe ermittelt werden soll, bestimmen die Schnittpunkte einer Parabel mit einer Geraden oder einer anderen Parabel grafisch oder rechnerisch, wandeln quadratische Terme zwischen der allgemeinen Form und der Scheitelpunktform um und nutzen dabei geeignete Umformungsregeln.	Ich kann eine quadratische Funktion in einer Tabelle, einem Graphen oder einer Gleichung darstellen und passende Werte berechnen. Ich kann die besondere Form des Graphen einer quadratischen Funktion (Parabel) beschreiben und erklären, wie sich der Graph verändert, wenn sich die Zahlen im Term ändern. Ich kann den Scheitelpunkt und die Achsensymmetrie einer Parabel erkennen und ihre Bedeutung in einer Situation erklären. Ich kann die Nullstellen (Schnittpunkte mit der x-Achse) einer Parabel bestimmen, indem ich den Graphen anschaue oder rechne. Ich kann erklären, wann eine quadratische Gleichung zwei, eine oder keine Lösung hat, und dafür Beispiele geben. Ich kann eine quadratische Gleichung durch Ablesen am Graphen oder durch Rückwärtsrechnen lösen, wenn der Term in Scheitelpunktform gegeben ist. Ich kann eine quadratische Gleichung rechnerisch lösen und einen passenden Lösungsweg auswählen, z B. mit binomischen Formeln oder durch Umformen. Ich kann eine quadratische Gleichung aufstellen, wenn in einer Aufgabe oder einer Situation eine Größe gesucht ist. Ich kann die Schnittpunkte einer Parabel mit einer Geraden oder einer anderen Parabel bestimmen, grafisch oder rechnerisch. Ich kann zwischen der allgemeinen Form und der Scheitelpunktform einer quadratischen Funktion wechseln, indem ich die passenden Umformungen durchführe.	Auf diesen Seiten sind Ideen, wie quadratische Funktionen und Gleichungen sprachsensibel eingeführt werden können und Diagnose- und Fördermaterial stehen zur Verfügung: https://maco.dzlm.de/verstehensgrundlagen-zu-funktionen https://maco.dzlm.de/sites/maco/files/material-lul/dzlm_difsek_funktionen_regelschul_quadr_fkt_240109_0.pdf
					Potenzfunktionen Die Lernenden erkennen Potenzfunktionen der Form f(x)=a⋅xb in Graphen, Termen oder Tabellen und beschreiben deren typisches Wachstum oder Verhalten, nutzen Potenzfunktionen, um geeignete Realsituationen zu beschreiben, verwenden digitale Werkzeuge (z B. Tabellenkalkulation oder Funktionsplotter), um Potenzfunktionen darzustellen und deren Eigenschaften zu untersuchen.	Ich kann Potenzfunktionen der Form f(x)=a⋅xb in Graphen, Termen oder Tabellen und deren typisches Wachstum oder Verhalten beschreiben. Ich kann Potenzfunktionen nutzen, um geeignete Realsituationen zu beschreiben. Ich kann digitale Werkzeuge verwenden (z B. Tabellenkalkulation oder Funktionsplotter), um Potenzfunktionen darzustellen und deren Eigenschaften zu untersuchen.
					Exponentielles Wachstum, z.B. Zinsen Die Lernenden stellen exponentielle Wachstumsprozesse in Tabellen, Graphen, Termen und eigenen Worten dar, wechseln zwischen den Darstellungen und benennen deren Vor- und Nachteile, erklären Begriffe wie Anfangswert, Wachstumsfaktor, Zinssatz, Kapital nach n Jahren sowie Verdopplungs- oder Halbwertszeit in Bezug auf unterschiedliche Darstellungen, bestimmen fehlende Werte in exponentiellen Zusammenhängen rechnerisch oder grafisch und nutzen dabei auch digitale Werkzeuge, wenden exponentielle Funktionen zur Bearbeitung realitätsnaher Problemstellungen an, z B. bei Zinseszinsrechnung, Bevölkerungswachstum oder Zerfallsprozessen.	Ich kann exponentielles Wachstum in einer Tabelle, einem Graphen, einem Term und mit eigenen Worten darstellen und zwischen den Darstellungen wechseln. Ich kann erklären, was Anfangswert, Wachstumsfaktor, Zinssatz, Kapital nach mehreren Jahren, Verdopplungszeit und Halbwertszeit bedeuten, und wie man sie in einer Tabelle, einem Term oder einer Situation erkennt. ch kann fehlende Werte in exponentiellen Zusammenhängen berechnen oder aus einer Darstellung ablesen, auch mit digitalen Hilfsmitteln. Ich kann Aufgaben mit exponentiellem Wachstum lösen, z B. bei Zinsen, Bevölkerungswachstum oder Zerfall – mit Tabelle, Term oder Rechner. Ich kann den Unterschied zwischen linearem, quadratischem und exponentiellem Wachstum erklären und an Beispielen zeigen, wie unterschiedlich schnell sie wachsen.	Material Mathewerkstatt zu „Zinseszins und Exponentialfunktion“: http://www.ko-si-ma.de/front_content.php%3Fidcat=992&lang=12.html
					Trigonometrische Funktionen Die Lernenden verwenden die Sinusfunktion in der Form f(x)=asin(bx) zur Beschreibung periodischer Vorgänge mit Hilfe digitaler Medienwerkzeuge.	Ich kann erklären, was eine Sinuskurve ist und wie sie verläuft. Ich kann einfache periodische Vorgänge (z B. Schwingungen oder Wellen) mit der Sinusfunktion beschreiben. Ich kann mit einem digitalen Werkzeug (z. B. Funktionsplotter) eine Sinusfunktion darstellen und verändern.	Material Mathewerkstatt zu „Trigonometrie“: http://www.ko-si-ma.de/front_content.php%3Fidcat=992&lang=12.html In GeoGebra lasse sich die trigonometrischen Funktionen entdecken, z.B. https://www.geogebra.org/m/jBnVB9TB

Zum Inhaltsverzeichnis zurück

4. Führerscheine für die Hand der Kinder

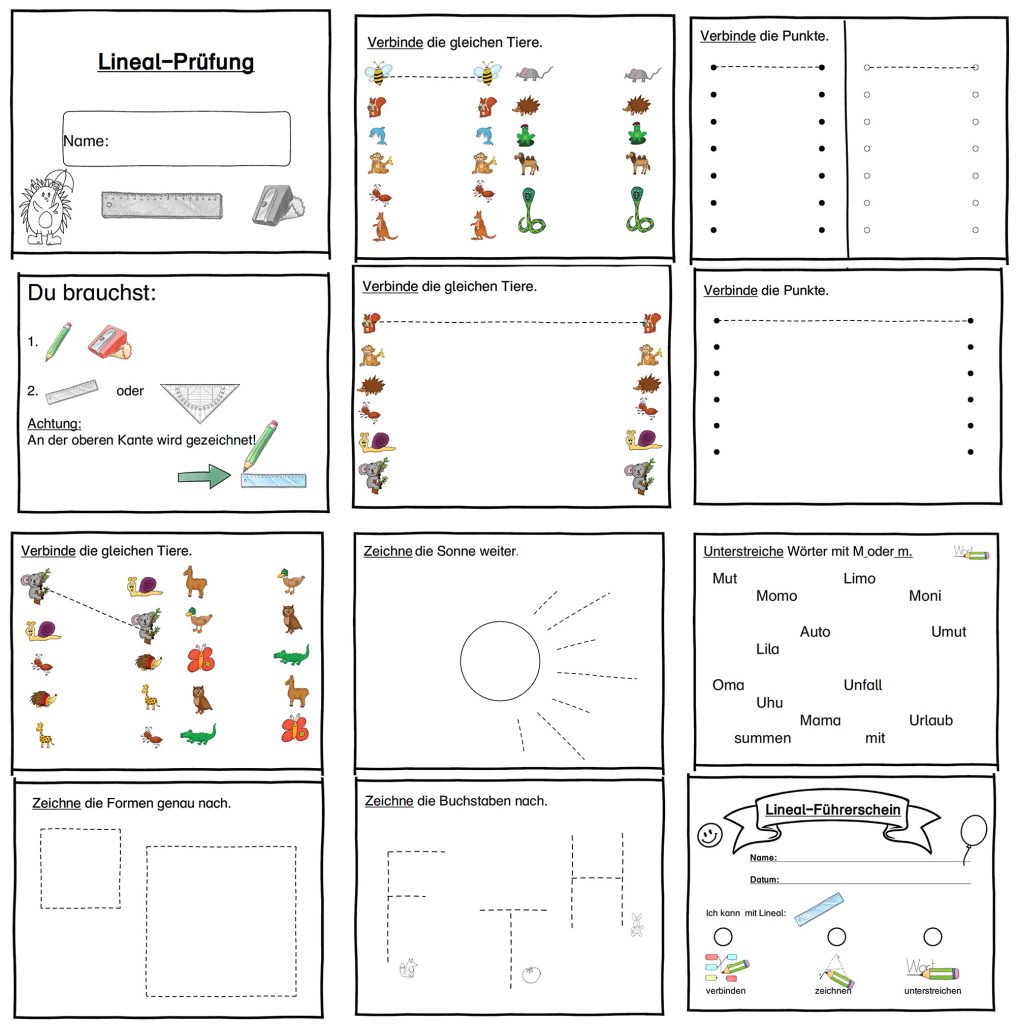
Durch die Arbeit mit Führerscheinen erhalten sowohl die Lernenden als auch die Lehrkräfte einen Überblick darüber, inwieweit Kompetenzen erreicht wurden. Die Führerscheine schaffen Transparenz über Lernziele und können aufgrund des überschaubaren Umfangs und spielerischer Formate die Motivation fördern und Selbstwirksamkeit stärken. Zugleich können sie der Dokumentation von Lernschritten dienen und zum Üben anregen. Nachfolgend werden zwei Führerscheine vorgestellt. Der erste Führerschein ist für die Grundrechnungen der Multiplikation, d.h. das kleine Einmaleins, gedacht. Er ist in der primaren Entwicklungsstufe einsatzfähig. Der zweite Führerschein ist der Lineal-Führerschein und ebenfalls auf der primaren Entwicklungsstufe anzuwenden. Diese Einblicke sind exemplarisch zu verstehen und in verschiedenen Formen adaptierbar.

Einmaleins Führerschein Download als PDF

Lineal Führerschein Download als P DF

Zum Inhaltsverzeichnis zurück

5. Exemplarische Entwürfe für das Lernen am gemeinsamen Gegenstand

Der Ansatz des Lernens am gemeinsamen Gegenstand geht u.a. auf ein Konzept von Feuser (1989) sowie auf Traditionen des Epochen- und Projektunterrichts zurück. Dahinter steht die Idee, dass alle Kinder gemeinsam zu einem Rahmenthema – dem Unterrichtsgegenstand – im lernen. Dabei können das Herangehen, die Aufgabe, die Prozessgestaltung und die Ergebnisse zwischen den Lernenden variieren. Bei der Unterrichtsplanung werden die individuellen Lernvoraussetzungen, der Lerngegenstand und die Aneignungsniveaus berücksichtigt. Mit diesem Ansatz des Lernens am gemeinsamen Gegenstand können Individualisierung, Differenzierung und die Festlegung von individuellen Lernzielen in heterogenen Lerngruppen umgesetzt werden und zugleich ist die Kooperation am gemeinsamen Gegenstand möglich.

Nachfolgend sollen zwei Beispiele einen Einblick in die Arbeit am gemeinsamen Gegenstand bieten. Vorgestellt werden a) das fächerübergreifende Apfelprojekt und b) die mathematische Lernumgebung zum Zählen und Bündeln.

a) Das fächerübergreifende Apfelprojekt mit den mathematischen Schwerpunkten „Zählen,“ (Zahl und Operation), „Formen und Muster legen, Dinge bauen“ (Raum und Form), „Verhältnisse und Vermutungen“ (Daten und Zufall) und „Wiegen und Vergleichen“ (Größen und Messen)

Im fächerübergreifenden Apfelprojekt können mathematische Zusammenhänge am Beispiel der Apfelernte fokussiert werden, so dass die Lernenden auf unterschiedlichen Niveaus gemeinsam ihre mathematischen Kompetenzen erweitern und vertiefen können. Gleichzeitig lernen sie alltagsbezogen die Ernte, Verarbeitung und den Umgang mit Äpfeln kennen und erleben dies selbst.
Bei der Planung der Lernumgebung berücksichtigen die Lehrkräfte zum einen die individuellen Entwicklungsniveaus und Lernzugänge und zum anderen die Struktur der Lerninhalte und deren Bedeutung für die Lernenden. Die Umsetzung erfolgt auf einem Erntehof für Äpfel. Die Lehrkräfte stellen verschiedene Materialien wie Körbe, Waagen, Säcke, Farben, Wasser, eine Presse, Eimer und ähnliches zur Verfügung. Den individuellen Lernständen entsprechend bereiten die Lehrkräfte Aufgaben(karten) und Stationen vor. Dabei sollten Pflicht- und Wahlstationen möglich sein, sodass die Lernenden auch frei nach Interessen entscheiden können. Die Aufgabenkarten sollten die Ziele der Lerneinheit umfassen und der Reflexion dienen, inwieweit sie erreicht wurden. An den Stationen können – je nach Komplexität der Aufgaben – Lehrkräfte zur Unterstützung der Lernenden Erklärungen geben, Hintergründe erläutern und ggf. weiterführende Aufgabenstellungen geben. Sofern es möglich ist, könnten auch Mitarbeitende vom Erntehof neben den Lehrkräften die Stationen begleiten. Als Expertinnen und Experten können sie Bildungsinhalte auf praxisnahe Weise vermitteln und dadurch den Unterricht erweitern und motivieren, z.B. können sie Einblicke in die Historie von Waagen und Geräten bei der Verarbeitung von Äpfeln bieten.

Die Aufgabenkarten sollten je nach Lernstand der Lernenden angemessen gestaltet sein, d.h. für manche sehr anschaulich und mit Bildern, für weiter fortgeschrittene Lernende ggf. auch mit schriftlichen Teilen, in denen sie Lernprozesse reflektieren und neue Erkenntnisse festhalten können. In jedem Fall sollte am Ende des Apfelprojekts ein individuelles Feedbackgespräch zwischen den Lehrkräften und den Lernenden stattfinden. Bei diesem werden neben den fächerübergreifenden (z.B. aus den Bereichen Deutsch, Biologie, Physik, Chemie) und sozialen Kompetenzentwicklungen, die das Projekt ermöglicht, auch die mathematischen Kompetenzen in den Blick genommen. Gemeinsam sollten Lehrkräfte und Lernende reflektieren, welche Kompetenzen erworben wurden und welche nächsten Stufen der Entwicklung nun individuell anstehen.

Zum Inhaltsverzeichnis zurück

m Folgenden wird gezeigt, wie die Lernziele der verschiedenen Zugänge aus den Stufenmodellen dem Thema entsprechend präzisiert werden können.

Lernende, die sich auf der basalen Bildungsstufe im Bereich der mathematischen Kompetenzentwicklung befinden, können u.a. folgende fachübergreifende Erfahrungen machen und Kompetenzen entwickeln:

Ich kann Äpfel pflücken und aufsammeln. Ich kann sie in den Korb legen.
Ich kann einen Apfel im Fühlsack ertasten und von anderen Dingen unterscheiden.
Ich kann aus der Apfelwanne die Kastanien, Bälle und Zierkürbisse heraussuchen.
Ich kann mit einer Apfelhälfte und Farbe drucken.
Ich kann die Äpfel waschen.
Ich kann große und kleine Äpfel sortieren.
Ich kann faulige Äpfel aussortieren.
Ich kann immer zwei Äpfel zum Korb bringen.
Ich kann beobachten, wie aus den Äpfeln kleine Apfelschnitzel entstehen.
Ich kann an der Presse drehen und sehen, dass Saft herausläuft.

Kinder, die sich auf der elementaren Bildungsstufe im Bereich der mathematischen Kompetenzentwicklung befinden, können u.a. folgende fachübergreifende Erfahrungen machen und Kompetenzen entwickeln:

Ich kann die Äpfel zählen.
Ich kann zählen, wie viele Äpfel in einen Eimer passen.
Ich kann die Äpfel der Größe nach sortieren.
Ich kann so viele Äpfel zum Korb bringen, wie auf der Zahlenkarte steht.
Ich kann die Äpfel zerschneiden und die Apfelchips zählen.
Ich kann mit Äpfeln einen Kreis, ein Viereck und ein Dreieck legen.
Ich kann Äpfel mit der Balkenwaage wiegen.

Kinder, die sich auf der primaren Bildungsstufe im Bereich der mathematischen Kompetenzentwicklung befinden, können u.a. folgende fachübergreifende Erfahrungen machen und Kompetenzen entwickeln:

Ich kann zählen, wie oft man pumpen muss, damit die Wanne bis zur Markierung mit Wasser gefüllt ist.
ch kann die Abfolge der Arbeitsschritte beim Apfelsaftpressen beschreiben.
Ich kann in Schritten zählen, wie viele Äpfel in einen Eimer passen.
Ich kann die Anzahl der Äpfel von fünf Eimern (einer Muserfüllung) ermitteln.
Ich kann mit Äpfeln eine Pyramide bauen und sagen, wie viele Äpfel ich benutzt habe.
Ich kann abwiegen, wie schwer die Äpfel, die Apfelschnitzel, die gepressten Apfelschnitzel und der Saft einer Muserfüllung sind.
Ich kann die Zahlen vom Wiegen vergleichen und Vermutungen anstellen.
Ich kann eine Sachaufgabe für meine Mitschüler formulieren.
Ich kann graphisch darstellen (z.B. mit Säulendiagrammen), wie viele Kilogramm Äpfel jede Klasse geerntet hat.

Ich kann zählen, wie oft man pumpen muss, damit die Wanne bis zur Markierung mit Wasser gefüllt ist.
ch kann die Abfolge der Arbeitsschritte beim Apfelsaftpressen beschreiben.
Ich kann in Schritten zählen, wie viele Äpfel in einen Eimer passen.
Ich kann die Anzahl der Äpfel von fünf Eimern (einer Muserfüllung) ermitteln.
Ich kann mit Äpfeln eine Pyramide bauen und sagen, wie viele Äpfel ich benutzt habe.
Ich kann abwiegen, wie schwer die Äpfel, die Apfelschnitzel, die gepressten Apfelschnitzel und der Saft einer Muserfüllung sind.
Ich kann die Zahlen vom Wiegen vergleichen und Vermutungen anstellen.
Ich kann eine Sachaufgabe für meine Mitschüler formulieren.
Ich kann graphisch darstellen (z.B. mit Säulendiagrammen), wie viele Kilogramm Äpfel jede Klasse geerntet hat.

Kinder, die sich auf der sekundaren Bildungsstufe im Bereich der mathematischen Kompetenzentwicklung befinden, können u.a. folgende fachübergreifende Erfahrungen machen und Kompetenzen entwickeln:

Ich kann die verschiedenen Ergebnisse beim Wiegen miteinander in Beziehung setzen und berechnen, ob es Verluste gibt. Ich kann vermuten, warum das so ist.
Ich kann für gekauften Apfelsaft berechnen, wie viele Äpfel für eine Flasche/ einen Kasten Saft gebraucht wurden. Ich kann das für die Produktionsmenge eines Tages berechnen.
Ich kann eine Sachaufgabe formulieren, bei denen meine Mitschüler berechnen müssen, wie viele LKW-Ladungen mit Äpfeln für eine Tagesproduktion gebraucht werden.
Ich kann graphisch darstellen, wie das Verhältnis von Äpfeln, Saft und ausgepressten Apfelschnitzeln ist.

Zum Inhaltsverzeichnis zurück

b) Eine mathematische Lernumgebung zum Zählen und Bündeln

Auch für die Planung von Lernumgebungen im Mathematikunterricht können die Stufenmodelle genutzt werden, z.B. für das Thema Zählen und Bündeln. Im Folgenden wird gezeigt, wie mithilfe der Stufenmodelle differenziert werden kann, so dass die Lernenden ein Zugang zum mathematischen Kompetenzerwerb erhalten, der ihren individuellen Lernvoraussetzungen entspricht. Anschließend folgen Überlegungen, wie gemeinsames Lernen ermöglicht werden kann. Die Beispiele sind entnommen aus Krähenmann et al. (2015).

In einer leistungsheterogenen Klasse soll das Thema Zählen und Bündeln erarbeitet werden. Einige Kinder haben den Zahlenraum bis 100 sicher erarbeitet und können flexibel addieren, subtrahieren und multiplizieren. Sie haben das Ziel im Zahlenraum bis 1000 zu zählen und zu bündeln.

Das Bündeln ist ein wichtiges Lernziel für Lernende mit primarem Zugang zum mathematischen Lerninhalt und Teilziele können der Tabelle entnommen werden:

Ich kann jeweils 10 Objekte (Zahlenwert „Einer“) zu einem Bündel zusammenfassen und verwende dazu den Zahlenwert „Zehner“. Ich bündle 12 Einer in einen Zehner und 2 Einer.
Ich kann 10 Zehner zu einem Hunderter bündeln.
Ich weiß, dass die erste Ziffer einer zweistelligen Zahl für die Anzahl der Zehnerbündel steht und die zweite Ziffer für die Einer. Das heißt, dass z. B. bei der Zahl 23 die erste Ziffer (2) für die Zehnerbündel und die zweite Ziffer (3) für die Einer steht. Die Zahl 23 besteht also aus 2 Zehnern und 3 Einern.

Für Lernende, die vor allem mit basalen Zugängen lernen, können aus der Tabelle z.B. die folgende Kompetenz ausgewählt und für den Umgang mit Mengen präzisiert werden:

Ich handele mit Gegenständen in meiner Umgebung und beginne sie zu vergleichen und zu unterscheiden, ob sie groß oder klein, kurz oder lang, schwer oder leicht sind.
Ich kann, wenn mir zwei Mengen gezeigt werden, mitteilen, wo mehr Gegenstände sind.
Ich kann fühlen, in welchem Säckchen nur ein Gegenstand ist und in welchem mehrere Gegenstände sind.
Ich kann hören, in welcher Dose nur ein Gegenstand klappert, wenn ich sie schüttle, und in welcher, mehrere Gegenstände sind.
Ich kann mich mit anderen darüber austauschen, ob es gleich viel Dinge sind oder nicht.

Für Lernende, die einen elementaren Zugang zum Inhalt erhalten sollen, ist das Herstellen immer gleich großer Bündel (z.B. 2er-, 3er- oder 4er-Bündel) eine bedeutende Unterrichtsaktivität, bei der sie eine größere Menge strukturieren und Zählprinzipien sowie die Zahl-Mengen-Verknüpfung festigen können. Der Tabelle können folgende Lernziele entnommen werden:

Ich vergleiche Dinge (hier Bündel) und kann sie auf Grund ihrer unterschiedlichen Merkmale (Größe, Gewicht, Länge usw.) sortieren und ordnen.
Ich kann kleine Mengen bis Vier auf einen Blick erkennen und das Zahlwort dazu nennen.
Ich kann mit anderen darüber sprechen, wie viel wir von etwas haben, wie viel wir brauchen usw.

Die Lernziele im sekundaren Zugang unterscheiden sich vom primaren Zugang durch den Zahlenraum und dadurch, dass die Lernenden sich die Bündelungen vorstellen können und nicht das Material zur Anschauung benötigen. Die Lernenden können sicherer und flexibler zwischen den verschiedenen Darstellungsarten hin und her übersetzen.

Ich kann Zahlen, die mit Material gelegt sind, und Zahlbilder lesen.
Ich kann Zahlen mit Material und Zahlbildern darstellen.
Ich kann bündeln und entbündeln.
Ich kann Zahlen in der Stellenwerttafel ablesen und darstellen.

Gemeinsame Lernsequenzen – von- und miteinander Lernen

Neben individuellen Arbeitsphasen in Gruppen oder Paaren sind Einstiegs- und Reflexionssequenzen als gemeinsame Phasen für den Austausch geeignet. Zum Thema Zählen und Bündeln eignet sich als Einstieg ein Schätzwettbewerb, bei dem den Lernenden drei Gläser mit unterschiedlich vielen Gegenständen präsentiert werden. Während Lernende mit basalem Zugang die Unterschiede wahrnehmen und ggf. bestimmen, in welchem Glas sie die meisten Gegenstände vermuten, bringen Lernende mit elementarem Zugang die Gläser in eine Reihenfolge. Lernende mit primarem und sekundaren Zugang schätzen Zahlen, notieren sie und versuchen ihre Schätzung zu begründen. Gemeinsam planen die Lernenden, wie sie bei der Anzahlbestimmung vorgehen wollen. In der Reflexionsphase können sie ihre Erkenntnisse zu Zähl- und Bündelungsstrategien einander mitteilen und diskutieren.

Zum Inhaltsverzeichnis zurück

6. Entwürfe für die Arbeit an Themen und Interessen der Kinder

Durch die bewusste Gestaltung von motivierenden pädagogischen Settings, kann das mathematische Interesse der Lernenden geweckt und erweitert werden. Durch Beobachtungen kann das Interesse der Lernenden in Situationen mit bestimmten Themen, Aktivitäten und Materialien häufig erkannt werden. Zum Beispiel kann in Zählsituation oder bei Würfelspielen beobachtet werden, ob die Lernenden ein Interesse an Zahlen und Mengen zeigen. Auch Materialien, die zum Handeln anregen, Kunstprojekte, Bilderbücher, (Rollen-)Spiele und Alltagssituationen können das Interesse an Mathematik wecken und freudvolle Erfahrungen ermöglichen.

Sie können in verschiedenen Organisationsformen, z.B. Freiarbeit und Lerntheke, aufbereitet werden und es den Lernenden ermöglichen, Thema und Material, sowie Zeitumfang und Verständnistiefe zu wählen.

Nachfolgend werden exemplarisch einige konkrete Materialhinweise formuliert.

Alltagsmaterialien

Materialwimmelkisten

Zusammenstellung verschiedene Elemente, die in großer Anzahl zur Verfügung stehen können (Knöpfe, Steine, Kastanien, Stäbchen, Würfel usw.).

Diese Materialvielfalt kann in einer schönen (verschließbaren Kiste) innerhalb der Lerntheke angeboten werden. Es lädt ein zu Materialerfahrungen, zum Klassifizieren, zur Reihenbildung, zum Gestalten von Mustern, zu mathematischen Operationen und führt in der Regel zu einer angeregten Interaktion zwischen den Lernenden, die zeitgleich auf ihren Lernniveau mit den Materialien umgehen.

Schätzglas

Ein großes Glas mit gleichartigen Materialien als Anregung für die Lernenden zum Schätzen der Anzahl.

Dieses Schätzglas kann für ritualisiert im Tagesgeschehen Beachtung finden. Die Lernenden werden angeregt, ihre Vorstellungen von Anzahlen zu formulieren, weiterzuentwickeln und sich über die verschiedenen Hypothesen auszutauschen. Eine gemeinsame Überprüfung unter Beachtung der verschiedenen Vorgehensweisen in einer kleinen Gruppe kann die Lernenden zu immer kompetenterem Handeln anregen.

Naturmaterialien

Selbst gesammelte und zusammengetragene Früchte, Stöckchen, Steine, Blüten, Blätter usw., die saisonal ausgetauscht werden können und gut sortiert in schönen Schalen präsentiert werden.Zugleich können die Lernenden Materialerfahrungen sammeln.

Diese Materialien eigenen sich, um damit zu zählen, sie zu vergleichen und nach der Größe zu ordnen, sie zu wiegen und nach Gewicht zu ordnen, nach Merkmalen zu ordnen (schwimmt?). Naturmaterialien können auch als Stellvertreter für mathematische Größen (ein Stöckchen kann ein Zehner sein), zum Legen von symmetrischen Bildern, zum Befüllen von Gefäßen oder zum Darstellen von Mathematikaufgaben genutzt werden.

Einige weitere Beispiele für Interessen weckende Spiele und Karteien werden im Folgenden aufgezählt:

Wimmelbücher, Origamibücher/ Bücher zum Papierfalten
Eric Carle: „Die kleine Raupe Nimmersatt“ (Oettinger Verlag)
Eileen Christelow: „The five little monkeys“
B. Tenzler, I. Friebel: „Zappel und die Zauberzahlen“ (Kinderbuchverlag)
John O’Leary: „Zehn fahr’n mit der Eisenbahn“
Ernst Jandl: „Fünfter sein“ (Beltz & Gelberg)
Janosch: „Oh wie schön ist Panama“ (Beltz)
H. M. Enzensberger, R. S. Berner: „Der Zahlenteufel“ (Hanser)
Birgit Wenz, „Kinderleichte Becherküche“
Paolo Fiz: „Ein Weiser, ein Kaiser und ganz viel Reis“(Atlantis)
G. Schwenke, S. Scholz: „Die traurige Null“
Istvan Banyai: Zoom“ und „Re-Zoom“

Die Spiele und Kinderbücher können entsprechend der Interessen und Themen der Lernenden präsentiert und temporär ausgewechselt werden, um Reizüberflutungen zu vermeiden und immer wieder neue Herausforderungen anzubieten.

Zum Inhaltsverzeichnis zurück

7. Kommentierter Überblick über Stufenmodelle

„Im Mathematikunterricht entwickeln die Schülerinnen und Schüler in der aktiv-konstruktiven Auseinandersetzung mit sowohl anwendungs- als auch strukturorientierten mathematischen Fragen ein gesichertes Verständnis mathematischer Inhalte. Sie enthalten Zeit und Raum, selbst Probleme zu lösen und über Mathematik zu kommunizieren. Sie erwerben grundlegende mathematische Kompetenzen, mit denen sie ihre Lebenswirklichkeit aus der mathematischen Perspektive erschließen, um entsprechenden Anforderungen der Alltagswelt gerecht werden zu können.“ (KMK 2012, S.12)

m Vorhaben „Reckahner Modelle zur inklusiven Unterrichtsplanung“ wird angestrebt, die Vorgaben der KMK so aufzufächern, dass Hilfsmittel erarbeitet werden, die für alle verschiedenen Lernenden in heterogenen Lerngruppen Zugänge zu den mathematischen Lernbereichen anbieten. Sie sollen die innere Differenzierung im Unterricht unterstützen.

Das Fach Mathematik dient der Vermittlung von mathematischen Fähigkeiten, von mathematischer Bildung sowie der Fähigkeit mathematische Einsichten alltäglich aktiv zu nutzen; bisweilen wird von „mathematical literacy“ (Schneider/Küspert/Krajewski 2021, S. 131) gesprochen. Darunter wird nicht nur die Beherrschung mathematischer Operationen und des bereichsspezifischen Faktenwissens gefasst, sondern auch, in welchem Ausmaß mathematische Kompetenzen flexibel und funktional zur Lösung kontextbezogener Anforderungen eingesetzt werden können (vgl. ebd.). Für den inklusiven Unterricht im Fach Mathematik wurden im Rahmen des REMI-Projekts (Reckahner Modelle zur Inklusiven Unterrichtsplanung) eine Reihe diagnostisch-didaktischer Hilfsmittel entwickelt: Stufenmodelle für das Lernen in den basalen, elementaren, primaren und sekundaren Bildungszugängen, Führerscheine für die Hand der Kinder, Vorschläge für das Lernen am gemeinsamen Gegenstand in heterogenen Lerngruppen sowie Vorschläge für die Arbeit an Themen und Interessen der Kinder. Diese Entwürfe werden ergänzt um kurze Informationen zu weiteren Stufenmodellen und weiterführende Literaturangaben.

Zunächst wird im Folgenden die Arbeit mit einem tabellarischen REMI-Stufenmodell erläutert. Ziel des Stufenmodells ist es, ein Hilfsmittel für die didaktische Diagnostik zu sein. Zur Erarbeitung des Reckahner Stufenmodells wird die Unterscheidung der KMK in allgemeine mathematische und inhaltsbezogene mathematische Kompetenzen aufgegriffen und ineinander verwoben. Dies erscheint sinnvoll, um ein für die Praxis anwendbares Instrument zu schaffen, dass mehrperspektivisch die allgemeinen mathematischen und die inhaltsbezogenen Kompetenzen gleichzeitig fokussiert. Beide Kompetenzarten müssen die Lernenden entwickeln, wobei die Ausbildung und die Entwicklung der beiden unterschiedenen Kompetenzarten nicht losgelöst voneinander erfolgen können. Zu den allgemeinen mathematischen Kompetenzen im Primarbereich zählen laut KMK (2022a) „Mathematisch argumentieren, Probleme mathematisch lösen, mathematisch modellieren, mathematische Darstellungen verwenden, mit symbolischen, formalen und technischen Elementen der Mathematik umgehen und mathematisch kommunizieren“ (KMK 2022a, S. 8); die inhaltsbezogenen Kompetenzen werden auch als die zentralen Leitideen bzw. Teilbereiche bezeichnet: I. Zahl und Operation, II. Raum und Form, III. Muster und Strukturen, IV. Größen und Messen, V. Daten, Häufigkeit und Wahrscheinlichkeit. Im Stufenmodell werden die inhaltsbezogenen Kompetenzen als Strukturierung des Modells genutzt. Eine Zusammenführung der allgemeinen mathematischen Kompetenzen und der inhaltsbezogenen Kompetenzen wird realisiert. Diese Zusammenführung wird so gelöst, dass die inhaltsbezogenen Kompetenzen des als Teilüberschriften verwendet werden z.B. „Zahl und Operation“. Die allgemeinen mathematischen Kompetenzen werden darin eingeflochten.

Der Aufbau der grundlegenden mathematischen Kompetenzen beginnt wie der Aufbau und Erwerb aller Kompetenzen mit Vorerfahrungen, dem Generieren von sogenanntem Vorwissen. Bevor Kinder beispielsweise. Probleme unter Rückgriff auf mathematisches Wissen oder sogenannte mathematische Probleme lösen können, müssen sie bereits eine Idee darüber entwickelt haben, dass sie Probleme im Allgemeinen lösen können. Vergleichbares gilt für die grundlegenden Kompetenzen: Kommunizieren, Argumentieren, Modellieren und Darstellen. Deshalb beginnt das Aufzeigen von basalen Zugängen zum Erwerb der angestrebten allgemeinen Kompetenzen mit eher alltäglichen, lebensweltbezogenen, noch nicht unbedingt spezifisch mathematischen Zugängen.

Zugleich muss festgehalten werden, dass die Entwicklung der mathematischen Kompetenzen nicht in Form gleichförmiger Stufen angemessen verstanden werden kann. Vielmehr ist es ein Suchen, Finden, Festigen, Probieren und Weiterentwickeln – mitunter darf es auch Rückschritte geben, die auch dazu führen können, neue Einsichten zu gewinnen, die das Erzielen einer nächsten Stufe möglich machen kann. Es ist zum Beispiel möglich, dass sich Lernende in bestimmten Bereichen auf der elementaren Kompetenzstufe und in anderen Bereichen auf der primaren Kompetenzstufe befinden. Auf manchen Stufen wird das Kind lange verharren, bevor es nächste Entwicklungsschritte nehmen kann, für andere wird es eher kurze Zeit benötigen. Auch ist es möglich, dass Lernende eine weitere Unterteilung einzelner hier vorgestellter Stufenabschnitte benötigen. Dann wäre es sinnvoll, einzelne Teilkompetenzen zu unterteilen , um dennoch Entwicklung sichtbar zu machen. Die Entwicklung der Lernenden muss also prozesshaft, individualisiert und reflektiert werden.

ReMi-Materialien wurden entwickelt für den Unterricht in heterogenen Lerngruppen. Sie unterstützen Lehrkräfte darin, die aktuellen Lernstände der einzelnen Kinder und Jugendlichen in den Teilbereichen mathematischer Bildung unmittelbar zu erkennen und zu benennen. Infolgedessen können sie den Lernenden passende Materialien für individuelles und/oder Partner- und Gruppen-Lernen, beispielsweise in der Freiarbeit oder im Lernbüro, anbieten. Darüber hinaus lassen sich gemeinsam mit den Kindern die jeweils passenden Lernziele, Methoden und Unterstützungsleistungen im Sinne des Lernens am gemeinsamen Gegenstand klären. Dabei ist zu beachten: Stufenmodelle stellen mathematische Lernhandlungen in mehreren Teilbereichen getrennt dar, aber in Lernprozessen können sich Kompetenzen und Handlungen aus verschiedenen Teilbereichen auch überschneiden. Dies ist darin begründet, dass reale Handlungen immer auch Aspekte enthalten, die gerade nicht im Fokus stehen.

Im Folgenden wird zunächst die Spezifik der verschiedenen im REMI-Projekt konzipierten Zugänge zu mathematischen Kompetenzen erläutert.

7.1: Basaler Zugang zum mathematischen Kompetenzerwerb

Basale mathematische Bildungserfahrungen können sich Kinder dann besonders gut aneignen, wenn sie stabile emotionale Beziehungen erleben und aus dieser Sicherheit heraus, sich selbst und die unmittelbare Umgebung kennenlernen. „Im Zusammenwirken von Wahrnehmung und Bewegung entwickeln sich komplexer werdende (kognitive) Fähigkeiten. Die Freude am selbsttätigen und aktiven Ausprobieren und Entdecken führt zu einer Erweiterung des Aktionsraumes und der sozialen Beziehungen“ (Freistaat Thüringen 2015, S. 16). Basales Lernen geschieht auf individuell unterschiedliche Weise und in individuell völlig unterschiedlichen Geschwindigkeiten. Es beinhaltet auch grundlegende mathematische Bildungserfahrungen, die sich zunächst im Nahraum der Kinder durch sinnliche Begegnungen ereignen. In alltäglichen interaktiven Begegnungen können Kinder vertraute Sinneseindrücke wiedererkennen und unterscheiden, was die Entwicklung von Basiskompetenzen für das Erkennen von Mustern und Strukturen ermöglicht. Interessante Effekte zu wiederholen, ergibt sich zunächst zufällig und wird zunehmend bewusster, wenn die Bezugspersonen dialogisch reagieren, die Lernenden ermuntern und Zustimmung signalisieren.
Die Freude am Agieren und Interagieren ermöglicht es den Kindern in verschiedenen Räumen mit unterschiedlichen Objekten und Materialien in Kontakt zu treten. Sie lernen dadurch, sich immer besser zu orientieren und können Bewegungs- und Wahrnehmungsprozesse immer bewusster initiieren. Ritualisierte Vorgänge im Tagesablauf unterstützen die Entwicklung von temporären Handlungsfolgen, vorausschauendem Denken und passenden Verhaltensweisen. Basales Lernen bezieht sich auch darauf, ein Gespür dafür zu entwickeln, ob Ereignisse erwartbar sind oder eher überraschend eintreten.

Je weiter sich die Kinder entwickeln, desto gezielter erkunden sie ihre Welt durch spezifisches und experimentelles Handeln. In diesem Rahmen bilden sie Hypothesen, die sie im Tun überprüfen. Zunehmend sind sie in der Lage, Anregungen der Bezugspersonen in ihre Handlungsabsichten einzufließen zu lassen. So können sie immer besser gemeinsame Eigenschaften von Objekten erkennen und so beispielsweise Gegenstände gleicher Form oder gleicher Farbe einander zuordnen oder gleiche Gegenstände nach deren Größe ordnen.

Die zunehmende Qualität der feinmotorischen Kompetenzen und die Entdeckerfreude führen dazu, dass sich Möglichkeiten der Kinder erweitern, Objekte und Materialien zu zerlegen und wieder zusammenzufügen. Dadurch erwerben sie Grundlagen für das Verständnis von Teil-Ganzes-Beziehungen, von Reversibilität und Zählbarkeit von verschiedenen Dingen, beispielsweise Körperteilen, Gegenständen etc. Das zufällige Erproben von Materialeigenschaften kann allmählich übergehen in den sachgerechten Gebrauch von Materialien und Werkzeugen. „Basale mathematische Bildungsprozesse schließen somit die Entdeckung und Analyse von Mustern mit allen Sinnen und auch mit wachsender Abstraktheit ein“ (Freistaat Thüringen 2015, S. 164).
Die Entdeckung des eigenen Körpers und der Umwelt unterstützen die Begriffsbildung und schaffen die Grundlage für die Sprachentwicklung. Letztere wird vorranging und nahezu vollumfänglich durch den Dialog mit den erwachsenen oder jugendlichen Bezugspersonen unterstützt. Insgesamt steht im Zentrum der basalen Zugänge das Be-Greifen der Welt und das damit verbundene allererste Anbahnen mathematischen Darstellens und Verstehens.

7.2: Elementarer Zugang zum mathematischen Kompetenzerwerb

„Mathematische Bildung beinhaltet die Fähigkeit von Kindern und Jugendlichen, Phänomene und Probleme in spezifischer Weise wahrzunehmen und diese mit Hilfe mathematischer Konzepte zu durchdringen und zu lösen“ (Freistaat Thüringen 2015, S. 159).

Kinder erwerben Vorwissen und ganzheitliche Eindrücke, durch welche die mathematische Begriffsbildung vorbereitet wird. Elementare Zugänge schließen erweiterte Denk- und Handlungsmöglichkeiten der Kinder bezüglich komplexer werdender Sachverhalte ein. Durch eine handelnd-anschauliche Weltaneignung können die Kinder sowohl in informellen Alltagssituationen als auch in zunehmend non-formalen und ersten formalen Lernsituationen, beispielsweise in einem aktiv-entdeckenden Mathematikunterricht (vgl. Wittmann/Müller, 2022), mathematische Strukturen erkunden und formulieren. Sie können ihr Zahl- und Mengenverständnis entwickeln, erste Grundrechenerfahrungen im kleinen Zahlenraum machen und den Umgang mit Daten und Wahrscheinlichkeiten (im Sinne der Möglichkeit, dass Ereignisse eintreten) üben und so Erkenntnisse gewinnen. Typische Erfahrungen im Bereich des elementaren mathematischen Lernens sind die Freude an Zahlen, das erste Zählen, die Simultanerfassung kleiner Mengen, die Entdeckung der Invarianz, die Paarbildung, das Interesse am Ausprobieren und Experimentieren, das Konstruieren, das Erkunden von Unregelmäßigkeiten und Regelmäßigkeiten und der zunehmend kompetente Umgang mit symbolischen Darstellungen bis hin zur Nutzung von ersten mathematischen Symbolen und Zeichen.

Kinder eignen sich mathematische Kompetenzen in enger Verwobenheit von verschiedenen Inhalten und in unterschiedlichen Phasen an. Abhängig von ihrem je individuellen Vorwissen, den individuellen Zugängen im Zusammenhang mit den Anregungsqualitäten ihrer konkreten Umgebung erwerben die Kinder mathematische Kompetenzen. Die Verwendung von Zahlen und geometrischen Mustern beim Spielen, gemeinsame Betrachtung von Alltagsereignissen, die dialogische Aufarbeitung von Beobachtungen und anderes können zu Fragen, zum Beispiel über Mengenverhältnisse, über Zahlen und Zählstrategien oder zu Form- und Strukturbetrachtungen führen. Das Vermuten, das spielerische Prüfen und das Erkennen von dahinterliegenden Mustern können die Kinder auf je ihre eigene Weise zu neuen Fragen und Interesse am Bereich der Mathematik führen. Auch die Verknüpfung mit anderen Bildungsbereichen wie beispielsweise die naturwissenschaftliche, ästhetisch-kulturelle und sprachliche Bildung können das Interesse für Mathematik anregen.

Über Mathematik zu „philosophieren“ ist bei Kindern mit elementaren Bildungsbedürfnissen oftmals eine freudbetonte kognitive Herausforderung, die das genaue Betrachten, den kommunikativen Austausch, das Probleme erfassen und Lösungsstrategien finden thematisiert und langfristig Interesse für die Mathematik wecken kann (vgl. de Boer/Michalik 2018). Das Philosophieren mit Lernenden über Mathematik kann über alle Alters- und Kompetenzstufen hinweg erfolgen.

7.3: Primarer Zugang zum mathematischen Kompetenzerwerb

Die Erfahrungen der Kinder mit Mustern, Zahlen, Räumen und Wahrscheinlichkeiten bilden die Grundlage für die Erweiterung ihrer mathematischen Kompetenzen im primaren Zugang. Dabei verändert sich insbesondere die Darstellungsweise über zunächst eher handelnde, symbolische hin zu zunehmend abstrakteren Darstellungen von eigenen Erkenntnissen. Die Kinder entwickeln die Kompetenz, verständig mit bildlichen, symbolischen, materiellen, verbal-sprachlichen sowie grafisch-visuellen und tabellarischen Darstellungen, die mathematische Objekte und Sachverhalte repräsentieren, umzugehen und diese Darstellungen auch miteinander zu vernetzen, zu vergleichen, zu deuten und kritisch zu reflektieren.

Die gewonnenen Erkenntnisse werden nach und nach in der Sprache der Mathematik gefasst. Ebenso werden abstrakt-mathematisch formulierte Aussagen immer besser verstanden und mathematisch formulierbare Zusammenhänge zunehmend eigenständiger in der Fachsprache mündlich und schriftlich sowie mit Hilfe geeigneter Medien formuliert. Dazu gehört auch das Präsentieren, Beschreiben und strukturierte Darlegen eigener mathematischer Überlegungen, das Erläutern von Zusammenhängen und das kritische Hinterfragen von Erklärungen anderer (vgl. KMK 2022a, S. 10).

Mathematik wird von den Kindern im Kontext des primaren Zugangs mehr und mehr als eigene, auf das Erkennen, Durchdringen und Formulieren von Mustern und Zusammenhängen fokussierte Wissenschaft verstanden. Dabei beziehen sich die Erkenntnisse und Beschreibungen nicht mehr nur auf sichtbare arithmetische oder geometrische Muster und Zusammenhänge, sondern auch auf abstraktere oder verstecktere, weniger offensichtliche Muster (Strukturen, Beziehungen, Abhängigkeiten, Regelmäßigkeiten etc.). Die Mathematik wird damit als Möglichkeit erfahren, um Erscheinungen der Welt aus Natur, Gesellschaft, Kultur, Beruf und Arbeit auf eine Weise wahrzunehmen und zu verstehen, sie als geistige Schöpfung zu erleben und heuristische Fähigkeiten zu entwickeln (vgl. KMK 2022a, S. 6). Im Bereich des mathematischen Modellierens können die Kinder Sachprobleme mit Hilfe der Mathematik angehen. Dazu muss es ihnen gelingen, Realsituationen in mathematische Begriffe, Resultate und Methoden zu übersetzen (vgl. ebd., S. 11). Die Kinder entwickeln eigene Vorstellungen über Muster und Zusammenhänge und beginnen, sich in der selbstständigen Anwendung mathematischer Konzepte wie beispielsweise allgemein verwendeter Verfahren und Strategien zu üben. Sie beginnen zu erkennen, dass sich ein und dasselbe Problem auf unterschiedliche Weise mathematisch darstellen und mittels unterschiedlicher Herangehensweisen lösen lässt. Neben routinierten Lösungswegen werden zunehmend auch kreative, neuartige Ideen entwickelt; dies wird kritisch reflektiert. Dazu kann das Kind das systematische Probieren erlernen, Analogien nutzen, rückwärts arbeiten, Skizzen erstellen oder Tabellen darlegen (vgl. KMK 2022a, S. 10f.).

Die Kinder beginnen, den Aufbau und die Struktur des Bereiches der natürlichen Zahlen zu begreifen und durchdringen den Aufbau des Dezimalsystems mit dem Stellenwertprinzip und Bündelungsprinzip. Ebenfalls wird verinnerlicht, dass mehrstellige Zahlen auf eine bestimmte, vereinbarte Weise gesprochen werden müssen. Die Rechenoperationen Addition, Subtraktion, Multiplikation und Division werden als eigene mathematisch-abstrakte Handlungen erlernt; Beziehungen zwischen den Rechenoperationen werden entdeckt, Rechenstrategien entwickelt, Verfahren automatisiert. Der erfolgreiche Umgang mit halbschriftlichen und schriftlichen Verfahren oder das Rechnen mit Größen werden geübt. Insgesamt wird ein sicherer Umgang mit den grundlegenden relevanten mathematischen Objekten angestrebt: im Bereich der Arithmetik u.a. mit den Zahlen, Symbolen, Termen und Gleichungen, im Bereich der Geometrie u.a. mit den Ecken, Kanten, Formen, Winkeln und Symmetrieachsen und im Bereich des adäquaten Einsatzes mathematischer Werkzeuge u.a. mit Lineal, Zirkel, Taschenrechner und Apps (vgl. KMK 2022a, S. 12). Dazu bedarf es Fakten- und Regelwissen einerseits und Flexibilität und sachgerechten Umgang mit mathematischen Objekten und Werkzeugen andererseits (vgl. ebd.).

Die Lernenden werden angeregt, ihre Erkenntnisse im Dialog miteinander zu thematisieren. Dabei entwickeln sie auch ein Bewusstsein für strittige Fragen zu mathematischen Gegenständen und ein Bedürfnis, diese überzeugend aufzuklären (vgl. KMK 2022a, S. 10). Mathematische Vorgehen zu hinterfragen, Aussagen zu prüfen, Vermutungen anzustellen und Begründungen zu versuchen, sind wichtige Arbeitsschritte dazu (vgl. ebd.). Wenn es gelingt, den primaren Zugang zur Mathematik erfolgreich in Bezug zu lebensnahen Situationen, auch aus den Interessen weckenden Kinderwelten, zu setzen und diese zugleich in der abstrakten Sprache der Mathematik darzustellen, können nachhaltige Verständnisprozesse angebahnt und weiterführende mathematische Fragen herausgefordert werden. Die Lernenden werden ermutigt, mathematisch kompetente Entscheidungen zu treffen, logische Schlussfolgerungen zu ziehen und mathematisch nachvollziehbar zu argumentieren. Ein Bildungsangebot, das den forschenden Zugang ermöglicht, das Be-Greifen anregt und eine konstruktive Fehlerkultur beinhaltet, kann anschlussfähiges, vernetztes und nachhaltiges Lernen und Anwenden von Mathematik ermöglichen (vgl. ebd., S. 6). Um dieses Ziel zu erreichen, müssen die Lernenden aktiv und selbstbestimmt das fachliche mathematische Lernen mitgestalten und dies auch in sinnvoller Abwägung im digitalen Raum begleitet realisieren dürfen (vgl. ebd., S. 8). Laut KMK können im Mathematikunterricht digitale Bildungsprozesse in der Primarstufe ermöglicht werden, indem fachliche Kompetenzen digital gefördert werden, „wichtige informatorische Kompetenzen für eine Teilhabe in der digitalen Welt ‚unplugged‘, d.h. in nicht-informatorischen Kontexten, gefördert werden und fachliche Kompetenzen für die kritische Reflexion und Einordnung von Informationen in verschiedenen Darstellungen genutzt werden“ (ebd.). Stets geht es im Unterricht auch darum grundlegende mathematische Verfahren zu üben und zu festigen, so dass sie möglichst sicher beherrscht werden, u.a. um den Anforderungen des Hauptschulabschlusses beziehungsweise des mittleren Bildungsabschlusses sowie grundlegender beruflicher Ausbildungsgänge zu entsprechen.

7.4: Sekundarer Zugang zum mathematischen Kompetenzerwerb

Prinzipiell werden im Bereich der basalen, elementaren und primaren Zugänge alle mathematischen Denk- und Darstellungsweisen angebahnt. Sie können in der Regel mindestens auf einer pränumerischen Ebene gelöst werden.

Übergreifendes Merkmal des sekundaren Zugangs ist ein erhöhter Abstraktionsgrad. Dies ermöglicht Zahlenbereichserweiterungen (rationale und irrationale Zahlen), das Lösen von Gleichungen oder auch das Darstellen von Funktionen in verschiedenen Varianten, da der unmittelbare Bezug zur Vorstellungskraft und Gegenständlichkeit nicht mehr notwendig gegeben sein muss. Es werden reale Probleme mit Hilfe von Mathematik gelöst, wozu wiederum die Übersetzungsleistung von Realsituationen in mathematische Begriffe, Resultate und Methoden notwendig wird. Dazu müssen die Lernenden Realsituationen strukturieren, vereinfachen, in mathematische Modelle übersetzen, bearbeiten, Ergebnisse mit Blick auf die Realsituation deuten und überprüfen sowie das Modell auf Stimmigkeit und Angemessenheit beurteilen (vgl. KMK 2022b, S. 11). Genutzt werden dabei sowohl Standardmodelle wie die proportionale Zuordnung als auch komplexere Modelle wie geometrische Konstruktionen, die Sinus- und Exponentialfunktion oder Zufallsexperimente (vgl. ebd.). Das Problemlösen auf einem hohen Abstraktionsgrad wird im sekundaren Zugang vorangetrieben. Das bedeutet, dass mathematische Probleme erkannt und formuliert, geeignete Heurismen in Form von vorläufigen Annahmen ausgewählt und sinnvolle Lösungswege entwickelt sowie umgesetzt werden (vgl. ebd.). Neben vorgegebenen Problemen können auch eigene Fragestellungen formuliert, Ergebnisse auf Plausibilität geprüft, kreative Lösungsansätze gesucht und Lösungswege reflektiert werden.

Die Argumentation der Lernenden wird u.a. durch Entwicklung von mathematischen Begründungen und Beweisen zunehmend abstrakter. Dies ermöglicht letztendlich auch das Vordringen in die Mathematik als Wissenschaft mit ihren verschiedenen Teilgebieten, wie Algebra, Analysis, Topologie etc. Die Lernenden erläutern, prüfen und begründen Lösungswege mit einfachen Plausibilitätsargumenten, inhaltlich-anschaulichen Begründungen und Argumentationsketten (vgl. KMK 2022b, S. 9). Um dies zu realisieren, muss die Kompetenz der mathematischen Kommunikation ausgebaut werden. Dazu gehört sowohl das Entnehmen von Informationen aus Texten, mündlichen Äußerungen und weiteren Quellen als auch das Darlegen von Überlegungen in mündlicher und schriftlicher Form (vgl. ebd., S. 10). Mathematische Erkenntnisse darzustellen und zu präsentieren ist daher eine wichtige Lernform im sekundaren Zugangsbereich. Die Lernenden gehen in diesem Zusammenhang mit mathematischen Darstellungen wie der grafisch-visuellen, der algebraisch-formalen, der numerisch-tabellarischen und der verbal-sprachlichen Darstellung um (vgl. ebd., S. 12). Standarddarstellungen werden angewandt, gedeutet und verglichen und können auch zu eigenen Darstellungen weiterentwickelt werden (vgl. ebd.).

Ein Bereich, der in den basalen und elementaren Zugängen kaum und im primaren Zugang einen wachsenden Anteil hat, ist das mathematische Arbeiten mit digitalen Medien. Dieser ist intensiv im sekundaren Zugang enthalten. Neben dem analogen Umgang (mit Schulbuch, Lineal, Modellen) des mathematischen Lernens ermöglicht der digitale Umgang den Einbezug digitaler Mathematikwerkzeuge und themenspezifische mathematikhaltige Medien (z.B. Apps, interaktive Lernangebote) (vgl. KMK 2022, S, 13). Auch allgemeine Medien (z.B. Videos, Präsentationsmedien) spielen eine Rolle beim mathematischen Lernen, um „mathematikhaltige Informationen zu bündeln, zu präsentieren und nach mathematischen Kriterien zu beurteilen“ (ebd.). Auseinandersetzungen zwecks „kritischer Prüfung von Informationen der digitalen Welt unter mathematischen Gesichtspunkten, der Verwendung digitaler Mathematikwerkzeuge (z.B. Tabellenkalkulation oder Geometriesoftware) und Lernumgebungen über die Erstellung und Gestaltung eigener allgemeiner Medien wie Videos und Präsentationen bis hin zur bewussten Verwendung, Entwicklung und Reflexion von Algorithmen mit Hilfe digitaler Medien“ (ebd.) sollten die Lernenden durchlaufen. Zu bedenken ist noch ein wichtiger Sachverhalt: in digitalen Medien werden auf vielfältige Weisen grundlegende mathematisch Fertigkeiten vermittelt, die besonders dann hilfreich sein können, wenn Lernende mathematische Verfahren im Unterricht nicht verstanden haben.

Es werden folglich im Bereich des sekundaren Zugangs eher weniger grundlegend neue Herangehensweisen, die zunächst handelnd erschlossen werden müssen, angebahnt, sodass sich der sekundare Zugang von den basalen, elementaren und primaren Zugängen vor allem durch die Komplexität sowie das hohe Abstraktionsniveau unterscheidet. Aus inklusionspädagogischer Perspektive sind neben dem sekundaren Zugang mit dem tendenziell abstrakten Charakter in allen Schuljahren auch basale, elementare und primare Zugänge hoch bedeutsam.
Die für den Hauptschulabschluss und den Mittleren Schulabschluss notwendigen Kompetenzen werden durch die Auseinandersetzung der Lernenden mit den Inhalten aller Teilbereiche erarbeitet. Entsprechend der individuellen Begabung, der persönlichen Neigung und bereits erlebter Sinnhaftigkeit werden die Lernenden ihr Wissen präsentieren und die Voraussetzungen für die genannten Abschlüsse erfüllen. Weiterführende Darlegungen zu den inhaltsbezogenen Kompetenzen des ersten und mittleren Schulabschlusses geordnet nach den inhaltlichen Leitideen der KMK sind in „KMK (2022b): Bildungsstandards für das Fach Mathematik (ESA und MSA)“ dargelegt und können dort vertiefend nachgelesen werden.

7.5: Weitere Stufenmodelle

Das hier vorliegende REMI-Stufenmodell orientiert sich an zahlreichen, bereits im Fachbereich Mathematik erarbeiteten, diskutierten, kritisierten und teilweise empirisch geprüften Modellen. Eine Auswahl dieser Modelle soll im Folgenden zusammengetragen werden, sodass individuelle Vertiefungen ermöglicht sind. Impulsgebend sind natürlich auch die Vorgaben der KMK hinsichtlich der allgemeinen und inhaltsbezogenen mathematischen Kompetenzentwicklungen in der Primar- und Sekundarstufe (KMK 2022a und b).

Zur Beschreibung der Entwicklung numerischer Kompetenzen gibt es verschiedene Modelle, die alle davon ausgehen, dass sich das Zahlverständnis über das Zählen und den Umgang mit Zahlen entwickelt. Wichtig anzumerken ist, dass Kompetenzstufenmodelle in der Mathematik auch umstritten sind, da nicht von einer linearen Entwicklung der mathematischen Kompetenzen ausgegangen werden kann. Auf diese Problematik wurde bereits weiter oben eingegangen. Im Folgenden werden ausgewählte Modelle benannt, die zur Vertiefung des Themas einladen; die Liste ist selbstverständlich nicht als abschließend zu betrachten, sie kann lediglich Impulse geben.

Das Logical-foundations-Modell nach Piaget (Piaget/Szeminska 1975)
Dieses zu seiner Entstehungszeit bahnbrechende Modell fokussiert die Entwicklung des kardinalen und ordinalen Zahlenbegriffs. Folgeforschungen schlossen sich an (u.a. Brainerd 1979).

Das Skill-Integration-Modell der Zahlbegriffsentwicklung (Clements 1984)
Dieses Modell schaut auf die Kompetenz des Zählens und beginnt mit dem Erwerb der Zahlwörter. Wichtige Vertreter waren u.a. Gelman/Gallistel (1978), Fuson (1988) und Resnick (1989). Beispielhaft sei das Modell von Fuson zu den Phasen der Zählentwicklung skizziert. Man geht davon aus, dass sich Kinder auf mehreren Stufen gleichzeitig befinden können und die Zählkompetenz vom Zahlenraum abhängt. Die Zählentwicklung ist in fünf Phasen unterteilt:

Undifferenziertes Wortganzes: Zahlkette wird aufgesagt, aber nur als Ganzes; Zahlen werden beim Zählen nicht als getrennt wahrgenommen
Unzerbrechliche Kette: Zahlkette wird aufgesagt, aber als Wahrnehmung getrennter Wörter, die aneinanderhängen; eindeutige Zuordnung von Zahlwort zu Objekt wird möglich; Ende des Zählens wird als Kardinalwert erkannt
Aufgebrochene Kette: Zählbeginn kann beliebig sein, Kardinalwert als Beginn wird als Teilmenge bewusst; Zahlwörter werden einzeln wahrgenommen; später auch rückwärts zählen
Numerische Kette: Zahl wird als Einheit im numerischen Sinn gesehen, erstes Rechnen durch Abzählen an den Fingern durch Hoch- und Runterzählen (noch kein Verständnis der Rechenoperationen)
Vorwärts-Rückwärts-Kette: Bewusstwerden der Umkehrbarkeit von Addition und Subtraktion, d.h. vorwärts und rückwärts zählen, operieren mit dem numerischen Teil-Ganzen-Schema (d.h. zerlegen von Zahlen in verschiedene Komponenten); zählen als eine aber nicht einzige Strategie des Rechnens

Das Entwicklungsmodell von Krajewski (2003, 2005, 2007), das. sog. Entwicklungsmodell der Zahl-Größen-Verknüpfung (ZGV-Modell)

Das Modell betont, dass das kardinale Zahlverständnis ein fortschreitender Prozess ist, der zuerst in einem kleineren Zahlenraum stattfindet und dann auf höhere Zahlenräume übertragen wird. Es hat den Anspruch die Entwicklung des Zahlverständnisses von der Geburt bis ins Sekundarstufenalter abzubilden (Krajewski/Ennemoser, 2013).

Das Modell ordnet Teilkompetenzen, die für die für die Verknüpfung von Zahl und Anzahl notwendig sind, in drei Ebenen. Die Teilkompetenzen können sich zunächst isoliert entwickeln und werden zunehmend miteinander verknüpft zu Kompetenzen auf einer höheren Ebene.

Auf der Ebene der Basisfertigkeiten liegt zum einen die angeborene Fähigkeit, Mengen aufgrund ihrer unterschiedlichen Ausdehnung oder Fläche bzw. ihres Volumens grob voneinander zu unterscheiden, das sogenannte „subitizing“. Zum anderen werden die Zahlwörter und die Zahlwortreihe erworben, letztere jedoch ohne kardinales Verständnis. Diese Teilkompetenzen sind die Grundlage für das einfache Zahlverständnis auf Ebene 2, bei dem Zahlwörter mit Mengen verknüpft werden. Die Entwicklung des kardinalen Zahlbegriffs lässt sich in zwei Phasen unterteilen; zunächst entwickelt sich die unpräzise und anschließend die präzise Mengenvorstellung. Auf Ebene 3 wird das tiefe bzw. relationale Zahlverständnis erworben, d.h. die Einsicht in Zahlbeziehungen. Dazu gehören die Zerlegung und Zusammensetzung von Zahlen (z.B. 5 setzt sich aus 2 und 3 zusammen) sowie die Differenz zwischen zwei Zahlen (z.B. der Unterschied zwischen 3 und 5 ist 2). Diese Einsicht in die Beziehung zwischen einem Ganzen und seinen Teilen gilt als wichtige Voraussetzung für den Erwerb der Addition und Subtraktion.

Trotz des hierarchischen Aufbaus des Modells bildet es keine starre Entwicklungslogik ab und Entwicklungen können auf den verschiedenen Ebenen auch parallel verlaufen, abhängig vom Zahlenraum und von der Repräsentationsform der Aufgaben.

Das Modell der mathematischen Kompetenzentwicklung nach Fritz und Ricken (2008)

Dieses Modell knüpft an oben dargelegtes von Krajewski an. Es umfasst folgende fünf Stufen:

Stufe 1: Reihenbildung und Mengenvergleich (dies gilt als Vorbereitung des Rechenlernens und enthält u.a. das Ordnen von Objekten und das Erlernen von Zahlwörtern (Anknüpfung an Fuson).
Stufe 2: ordinaler Zahlenstrahl und zählendes Rechnen (dies impliziert die Unterscheidung von Zahlwörtern, das Eins-zu-eins-Prinzip (Anknüpfung an Resnick/Gallistel), die Arbeit mit Vorgänger-Nachfolger.
Stufe 3: kardinale Mengenvorstellung (dies umfasst beispielsweise das Wissen, dass die letzte Zahl alle anderen enthält sowie das Können von Addition und Subtraktion)
Stufe 4: Teil-Ganzes-Zerlegbarkeit (dies meint u.a. die Einsicht, dass Zahlen aus Mengen bestehen, die wiederum gegliederte Quantitäten enthalten, Teilmengen aus Gesamtmengen-Aufgaben und < und > Aufgaben)
Stufe 5: Relationaler Zahlbegriff und Teilmengenverständnis (dies umfasst u.a. die Erkenntnis, dass das Zahlwort für zusammengesetzte Mächtigkeiten steht und die Zahlwortreihe aus aufeinanderfolgenden Mächtigkeiten zusammengesetzt wird)

Das Stufenmodell von Aebli (1976)

Aeblis Stufenmodell sieht die genannten Entwicklungen nicht als Stufen, sondern vielmehr als „overlapping waves“ (Siegler 1998). Dies besagt, dass komplexe Kompetenzentwicklungen allmählich vollzogen werden und immer wieder Rückgriffe auf zuvor entwickelte Kompetenzen erfolgen. Das Modell sieht vier Phasen vor:

Phase 1: bei der Addition in der Anfangsphase wird noch auf Finger und andere Hilfsmittel zurückgegriffen
Phase 2: ständiger Rückgriff von der Zifferndarstellung auf den zugrunde liegenden anschaulichen Bedeutungsgehalt
Phase 3: symbolische Darstellung von Ziffern, im Kopf rechnen von Aufgaben
Phase 4: Automatisierung im Zeichenbereich
Verwiesen wird an dieser Stelle auch auf Untersuchungen mathematischer Kompetenzentwicklungen in der Grundschule von Reiss, Heinze, Pekrun und Ufer (vgl. Reiss/Heinze/Pekrun 2007, Ufer/Reiss/Heinze 2009). Zudem wurden unter Federführung von Werner Blum Kompetenzstufenmodelle für den Mittleren Schulabschluss und für den Hauptschulabschluss entwickelt (vgl. u.a. Prenzel/Blum 2007).

ILEA T-Stufenmodell Numeracy (Bartusch/Geiling 2015)

Im Rahmen des Forschungsprojekts ILEA T (Individuelle Lern-Entwicklungs-Analyse im Übergang von der Kita in die Schule) wurde die Entwicklung mathematischer Kompetenzen von Kindern mit Beginn des letzten Kindergartenjahrs bis zum Schulbeginn im Längsschnittdesign mittels eines dafür entwickelten standardisierten Verfahrens, dem diagnostischen Würfelspiel „Reise zu den Zahleninseln“, erfasst, wodurch die empirische Absicherung des theoretisch begründeten Stufenmodells ermöglicht wurde (vgl. Bartusch/Geiling 2015, S. 19-23). Das ILEA T-Stufenmodell Numeracy (ebd. S. 73 f.) ist in sieben Stufen gegliedert und beschreibt damit den untersuchten Ausschnitt der mathematischen Entwicklung von Kindern sehr detailliert. Die Kompetenzen werden innerhalb einer Stufe jeweils in Bezug auf die mathematischen Inhaltsbereiche beschrieben, die für Kinder der ausgewählten Altersgruppe besonders relevant sind: (1) Mengen (Mengen auffassen/bilden, Mengenrelationen, Zu-/Abnahme u.a.), (2) Anzahlen (Kardinalzahl, Anzahlbestimmung, Anzahlrelationen, Zahlrepräsentationen), (3) Zählen (Zahlwortreihe, Zählprinzipien, Ordinalzahlaspekt, …) und (4) Rechnen (Rechenstrategien, von der konkreten Handlung bis zur symbolischen Operation, …) (ebd., S. 73f.). Das ILEA T-Stufenmodell Numeracy zeichnet den Entwicklungsweg der schulpflichtig werdenden Kinder in die Welt der Zahlen damit ausgehend von basalen Kompetenzen bis hin zu im Primarbereich erwarteten Fertigkeiten und Einsichten (z.B. Einsicht in das dekadische Positionssystem) nach. Das Modell kann für den begrenzten Abschnitt der mathematischen Entwicklung von Kindern im Übergang von der Kita in die Schule als entwicklungssensibel eingeschätzt werden. Es ist konzeptionell innerhalb der Idee einer didaktischen Diagnostik verortet (Bartusch u.a. 2018, S. 214). Es „soll den Pädagoginnen helfen, die Beobachtungen des Verhaltens einzelner Kinder einzuordnen, im Sinne der „Schon-Könnens“ zu deuten und passende Entwicklungsanregungen zu gestalten.“ (Bartusch/Geiling 2015, S. 72).

8. Literaturverzeichnis

Wichtiger Hinweis zu Internet-Quellen und Verknüpfungen (Links):
Die Komplexität mathematischer Kompetenzentwicklungen erfordern vertiefendes Wissen und zahlreiche Zugänge, die in einer Tabelle lediglich angedeutet werden können. Die Autorinnen verweisen entsprechend auf Materialien, die auf fachdidaktischer Grundlage forschungsbasierte und praxiserprobte Materialen und Konzeptionen zur Umsetzung im Mathematikunterricht zur Verfügung gestellt werden.

Es finden sich zahlreiche Verknüpfungen (Links) zu den bewährten Online-Materialien für den Mathematikunterricht (u.a. PIKAS, Primakom, Mahiko, Kira), die in Kooperation zwischen dem Ministerium für Bildung und Schule des Landes NRW, des Deutschen Zentrums für Lehrkräftebildung Mathematik (DZLM) und der Technischen Universität (TU) Dortmund entwickelt wurde. Videos, Handreichungen und konkrete Praxisanregungen können für das Selbststudium, für Unterricht und zum Austausch mit Lehrkräften oder Eltern genutzt werden.

Die Links wurden zum Zeitpunkt der Veröffentlichung abgerufen. Die Autorinnen können nicht gewährleisten, dass alle Links dauerhaft verfügbar sind. In diesem Fall wird empfohlen, zum DZLM (Deutsches Zentrum für Lehrkräftebildung Mathematik) Kontakt aufzunehmen. https://dzlm.de

Links zu bewährten Online-Materialien für den Mathematikunterricht:

PIKAS (Prozessbezogen, Inhaltsbezogen, Kompetenzorientiert, Anregung fachbezogener Schulentwicklung)
https://pikas.dzlm.de/kontakt
Primakom (Primarstufe Mathematik kompakt): primakom@dzlm.de
KIRA (Kinder rechnen anders): kira@dzlm.de
MaCo (Mathematische Basiskompetenzen fördern): https://maco.dzlm.de/
Mahiko (Mathehilfe kompakt): mahiko@dzlm.de
ADI (Arithmetik digital): https://adi.dzlm.de/
Mathe sicher können: https://mathe-sicher-koennen.dzlm.de/
SiMa (Sprachbildung im Mathematikunterricht): https://sima.dzlm.de/

Literaturverzeichnis:

ADI. (o.J.). Figurierte Zahlen. Abgerufen am 13.8.2025 von https://adi.dzlm.de/figurierte-zahlen.
ADI. (o.J.). Produktregel der Kombinatorik. Abgerufen am 13.8.2025 von https://adi.dzlm.de/kombinatorik/produktregel-der-kombinatorik
ADI. (o.J.). Rechengesetze. Abgerufen am 13.8.2025 von https://adi.dzlm.de/rechengesetze
ADI. (o.J.). Teilbarkeit. Abgerufen am 13.8.2025 von https://adi.dzlm.de/teilbarkeit
Aebli, H. (1976). Grundformen des Lehrens: Eine allgemeine Didaktik auf kognitionspsychologischer Grundlage (9. Aufl.). Klett.
Bartusch, S. & Geiling, U. (2015). Pädagogische Diagnostik für Kinder auf dem Weg in die Welt der Zahlen. In: Geiling, U., Liebers, K. &
Prengel, A. (Hrsg.), Handbuch ILEA T. Individuelle Lern-Entwicklungs-Analyse im Übergang. Halle: Martin-Luther-Universität, 62-94.
URL: (http://ilea-t.reha. uni-halle.de/das_handbuch_ilea_t/) (31.01.2024).
Bartusch, S., Geiling, U. & Simon, J. (2015). Reise zu den Zahleninseln. Ein Aufgaben-Set für Kinder im Übergang Kita – Grundschule zur Erhebung von Kompetenzen im Umgang mit Mengen und Zahlen. Manual. Halle: Martin-Luther-Universität. URL: (http://ilea-t.reha.uni-halle.de/anlagen_ zum_handbuch/mathematik/) (31.01.2024).
Bartusch, S., Geiling, U., Liebers, K. & Prengel, A. (2018). Didaktische Diagnostik in der inklusiven Schuleingangsstufe: Das Beispiel ILEA T. In: Walm, M., Häcker, T. H., Radisch, F. & Krüger, A. (Hrsg.) (i.E.), Empirisch-pädagogische Forschung in inklusiven Zeiten – Konzeptualisierung, Professionalisierung, Systementwicklung. Bad Heilbrunn: Klinkhardt, S. 211-222.
Barzel, B., Glade, M., & Klinger, M. (2021). Algebra und Funktionen: Fachlich und fachdidaktisch. Springer. https://doi.org/10.1007/978-3-662-61393-1
Brainerd, C. J. (1979). The origins of number concept. Praeger.
Clements, D. H. (1984). Training effects on the development and generalization of Piagetian logical operations and knowledge. Journal of Educational Psychology (76), 766-776.
De Boer, H. & Michalik, K. (2018). Philosophieren mit Kindern. Forschungszugänge und -perspektiven. Barbara Budrich.
DZLM. (o.J.). Digitale Pinnwand zum Operationsverständnis Multiplikation. Abgerufen am 11.2.2025 von https://www.taskcards.de/#/board/9b6c3d96-338e-450f-8e04-b5500538f2f9/view
DZLM. (o.J.). Mathe sicher können – Operationsverständnis: Natürliche Zahlen / Operationsverständnis. Abgerufen am 1.3.2025 von https://mathe-sicher-koennen.dzlm.de/material-primar/natürliche-zahlen/operationsverstaendnis
DZLM. (o.J.). Operationsverständnis – allgemein. Abgerufen am 11.2.2025 von https://mathe-sicher-koennen.dzlm.de/material-primar/natürliche-zahlen/operationsverstaendnis
DZLM. (o.J.). Wortspeicher zum Bündeln und Zehnersystem. Abgerufen am 1.3.2025 von https://mathe-sicher-koennen.dzlm.de/mskfiles/uploads/Dokumente/mskgs_n3a_7_wortspeicher.pdf
Etzold, H. (2017). Isometriepapier [Mobile App]. Abgerufen am 13.8.2025 von https://dlgs.uni-potsdam.de/apps/isometriepapier
Etzold, H. (2017). Klipp Klapp [Mobile App]. Abgerufen am 13.8.2025 von https://dlgs.uni-potsdam.de/apps/klipp-klapp
Fabricius, S., Rathgeb-Schnierer, E., & Schütte, S. (Hrsg.). (2009). Lerntagebücher im Mathematikunterricht. Oldenbourg.
Fetzer, M. (2016). Inklusiver Mathematikunterricht: Ideen für die Grundschule. Schneider Verlag Hohengehren.
Feuser, G. (1989). Allgemeine integrative Pädagogik und entwicklungslogische Didaktik. In: Behindertenpädagogik, 28(1), 4–48.
FÖDIMA & PIKAS (Hrsg.). (2024). Diagnostizieren und Fördern im mathematischen Anfangsunterricht: Hintergrundwissen, Diagnose- und Förderanregungen Arithmetik Klasse 1 und 2 [Creative Commons BY-NC-SA]. Abgerufen am 12.2. 025 von https://pikas.dzlm.de/pikasfiles/uploads/upload/Material/diagnose_und_foerderung/gesamtkonzept_foedima_mit_kartei/Standortbestimmungen_und_kartei/fodima_hr_240614_.pdf
Franke, M., & Ruwisch, S. (2010). Didaktik des Sachrechnens in der Grundschule (2. Aufl.). Spektrum Akademischer Verlag.
Freistaat Thüringen (2015). Thüringer Bildungsplan. Abgerufen am 04.11.2023, unter https://bildung.thueringen.de/bildung/bildungsplan.
Friedrich-Verlag (2023). Inklusiver Mathematikunterricht am gemeinsamen Gegenstand. https://www.friedrich-verlag.de/friedrich-plus/sekundarstufe/mathematik/zahlen-groessen/inklusiver-mathematikunterricht-am-gemeinsamen-gegenstand-54 (letzter Zugriff 22.12.2023)
Fuson, K. C. (1988). Children´s counting and concepts of number. Springer.
Gaidoschik, M. (2007). Rechenschwäche verstehen – Kinder gezielt fördern. Persen Verlag.
Gaidoschik, M. (2009). „Das muss man sich einfach merken“??? Schwierigkeiten mit dem Einmaleins: Einige Anregungen für Vorbeugung und Abhilfe. Abgerufen am 24.1.2025 von http://www.recheninstitut.at/wp-content/uploads/2011/10/einmaleins1.pdf
Gaidoschik, M. (2012). Viele Wege führen über den Zehner. Abgerufen am 1.3.2025 von http://www.recheninstitut.at/mathematische-lernschwierigkeiten/fordertips/zehneruberschreitung/
Gaidoschik, M. (2017). Einmaleins verstehen, vernetzen, merken: Strategien gegen Lernschwierigkeiten (4. Aufl.). Klett Kallmeyer.
Geiling, U.; Liebers, K. & Prengel, A. (2015). Handbuch ILEA T. Individuelle Lern-Entwicklung-Analyse im Übergang von der Kita in die Schule. Abgerufen am 04.11.2023, unter https://wcms.itz.uni-halle.de/download.php?down=34521&elem=2750160.
Gelman, R. & Gallistel, C. R. (1978). The child´s understanding of number. Harvard University Press.
GeoGebra. (o.J.). GeoGebra. Abgerufen am 13.8.2025 von https://www.geogebra.org/?lang=de
Götze, D. (2015). Sprachförderung im Mathematikunterricht. Abgerufen am 1.3.2025 von https://proprima.dzlm.de/pikasfiles/uploads/upload/Material/Haus_7_-Gute-Aufgaben/IM/Informationstexte/sprachfoerderung_goetze_text.pdf
Götze, D., & Stark, J. (2022). Partibo – Brüche leicht gemacht [Mobile App]. Abgerufen am 13.8.2025 von https://apps.apple.com/de/app/partibo/id1588419717
Götze, D., Selter, C., & Zanneti, E. (2019). Das KIRA-Buch: Kinder rechnen anders. Verstehen und Fördern im Mathematikunterricht. Klett Kallmeyer.
Häsel-Weide, U., Nührenbörger, M., Moser Opitz, E., & Wittich, C. (2013). Ablösung vom zählenden Rechnen. Klett Kallmeyer.
Haus der kleinen Forscher (Hrsg.). (2014). Mathematik in Raum und Form entdecken. Abgerufen am 10.4.2025 von https://www.stiftung-kinder-forschen.de/fileadmin/Redaktion/1_Forschen/Themen-Broschueren/Broschuere_Mathematik-in-Raum-und-Form_2014_akt.pdf
Hess, K. (2012). Kinder brauchen Strategien. Klett Kallmeyer.
Hoenisch, N., & Niggemeyer, E. (2019). Mathe-Kings (3. Aufl.). wamiki. Abgerufen am 12.1.2025 von https://wamiki.de/ausstellungen/mathekings/
IQB – Institut zur Qualitätsentwicklung im Bildungswesen. (o.J.). Lernaufgaben Mathematik Primar. Abgerufen am 10.3.2025 von https://www.iqb.hu-berlin.de/bista/WeiterentwicklungBiSta/Lernaufgaben/MathePrimar/?view=preview
Johnson, V. (2008). Mathe kann man anfassen! 225 Ideen und Materialien für den handlungsorientierten Anfangsunterricht. Verlag an der Ruhr. Abgerufen am 1.3.2025 von https://www.verlagruhr.de/mathe-kann-man-anfassen.html
Jütte, H. & Lüken, M. M. (2020). Mathematik inklusiv unterrichten – Ein Forschungsüberblick zum aktuellen Stand der Entwicklung einer inklusiven Didaktik für den Mathematikunterricht in der Grundschule. Zeitschrift für Grundschulforschung (14), 31-48.
Känguru der Mathematik. (o.J.). Wettbewerbsaufgaben. Abgerufen am 13.8.2025 von https://www.mathe-kaenguru.de/
Käpnick, F. (2020). Mathematiklernen in der Schule. Springer Spektrum.
Kaufmann, S. (2010). Handbuch für die frühe mathematische Bildung. Schroedel.
KIRA. (o.J.). Beispiele: Rechengeschichten. Abgerufen am 1.3.2025 von https://kira.dzlm.de/kira-check/kira-check/operationen/emirhan
KIRA. (o.J.). Bildliche Darstellungen. Abgerufen am 1.3.2025 von https://kira.dzlm.de/node/116
KIRA. (o.J.). Halbschriftliche Addition. Abgerufen am 1.3.2025 von https://kira.dzlm.de/node/118
KIRA. (o.J.). Operationsverständnis Multiplikation. Abgerufen am 11.2.2025 von https://kira.dzlm.de/arithmetik/operationsverständnis/operationsverständnis-multiplikation
KIRA. (o.J.). Schöne Päckchen. Abgerufen am 1.3.2025 von https://kira.dzlm.de/node/137
Kluge, A., & Gatzka, S. (2014). Adaption des Materials N4 A „Ich kann Multiplikations-Aufgaben finden und umgekehrt“. Abgerufen am 1.3.2025 von https://mathe-sicher-koennen.dzlm.de/mskfiles/uploads/material_primar/N4/mskgs_n4a_komplett.pdf
KMK (2012): Bildungsstandards im Fach Mathematik für die Allgemeine Hochschulreife (Beschluss der Kultusministerkonferenz vom 18.10.2012). 2012 https://www.kmk.org/ fileadmin/Dateien/veroeffentlichungen_beschluesse/2012/2012_10 18-Bildungsstandards-Mathe-Abi.pdf. – zuletzt aufgerufen am 09.05.2021.
KMK (2022a). Bildungsstandards für das Fach Mathematik Primarbereich. (Beschluss der Kultusministerkonferenz vom 15.10.2004, i.d.F. vom 23.06.2022). – zuletzt aufgerufen am 17.09.2025 unter: https://www.kmk.org/fileadmin/veroeffentlichungen_beschluesse/2022/2022_06_23-Bista-Primarbereich-Mathe.pdf
KMK (2022b). Bildungsstandards für das Fach Mathematik. Erster Schulabschluss (ESA) und Mittlerer Schulabschluss (MSA). Zuletzt aufgerufen am 17.09.2025 unter: https://www.kmk.org/fileadmin/veroeffentlichungen_beschluesse/2022/2022_06_23-Bista-ESA-MSA-Mathe.pdf
Koch, K., Schulz, A., & Jungmann, T. (2020). Überall steckt Mathe drin. Alltagsintegrierte Förderung mathematischer Kompetenzen für drei- bis sechsjährige Kinder. Ernst Reinhardt Verlag.
Kornmann, R. (2010). Mathematik: Für alle von Anfang an!. Klinkhardt.
KOSIMA. (o.J.). Handreichung mathewerkstatt 10. Abgerufen am 13.8.2025 von http://www.ko-si-ma.de/front_content.php%3Fidcat=992&lang=12.html
Krähenmann, H. et al. (2015). Gemeinsam lernen – individuell fördern: Differenzierung im inklusiven Mathematikunterricht. In A. Peter-Koop, T. Rottmann & M. Lüken (Hrsg.), Inklusiver Mathematikunterricht in der Grundschule. Mildenberger.
Krajewski, K. (2003). Vorhersage von Rechenschwäche in der Grundschule. Verlag Dr. Kovac.
Krajewski, K. (2005). Vorschulische Mengenbewusstheit von Zahlen und ihre Bedeutung für die Früherkennung von Rechenschwäche. In M. Hasselhorn, H. Marx & W. Schneider (Hrsg.), Diagnostik von Mathematikleistungen. Tests und Trends (Bd. 4), S. 49-70). Hogrefe.
Krajewski, K. (2007). Entwicklung und Förderung der vorschulischen Mengen-Zahlen-Kompetenz und ihre Bedeutung für die mathematische Schulleistungen. In G. Schulte-Korne (Hrsg.), Legasthenie und Dyskalkulie: Aktuelle Entwicklungen in Wissenschaft, Schule und Gesellschaft (S. 325-332). Winkler.
Krajewski, K. & Ennemoser, M. (2013). Entwicklung und Diagnostik der Zahl-Größen-Verknüpfung zwischen 3 und 8 Jahren. In M. Hasselhorn et al. (Hrsg.), Diagnostik mathematischer Kompetenzen (Tests und Trends, Jahrbuch der pädagogisch-psychologischen Diagnostik, Neue Folge, Bd. 11, S. 41–65). Göttingen: Hogrefe.
Krüger, K., Sikora, C., & Sill, H.-D. (2015). Didaktik der Stochastik in der Sekundarstufe I. Springer Spektrum.
Landesbildungsserver Baden-Württemberg. (o.J.). Beweisvarianten vom Satz des Pythagoras. Abgerufen am 13.8.2025 von https://www.schule-bw.de/faecher-und-schularten/mathematisch-naturwissenschaftliche-faecher/mathematik/unterrichtsmaterialien/sekundarstufe1/geometrie/pyth/beweise
Lerndokumentation Mathematik. (2009). Anregungsmaterialien für den Anfangsunterricht. Abgerufen am 10.4.2025 von https://www.pedocs.de/frontdoor.php?source_opus=2844
Lerndokumentation Mathematik. (o.J.). Anregungsmaterialien (Gesamtdokument). Abgerufen am 1.3.2025 von https://www.pedocs.de/volltexte/2010/2999/pdf/BE3B_Lerndokumentation_Mathematik_Anregungsmaterialien_gesamt_7.10.08_D_A.pdf
Leuders, J.; Leuders, T.; Prediger, S. & Ruwisch, S. (2017). Mit Heterogenität im Mathematikunterricht umgehen. Springer.
Linneweber-Lammerskitten, H. & Wälti, B. (2008). HarmoS Mathematik: Kompetenzmodell und Vorschläge für Bildungsstandards. Beiträge zur Lehrerbildung 26 (3), 326-337.
MaCo. (o.J.). Verstehensgrundlagen zu Funktionen (Jhg. 7–10). Abgerufen am 13.8.2025 von https://maco.dzlm.de/verstehensgrundlagen-zu-funktionen
MaCo. (o.J.). Verstehensgrundlagen zu Variablen, Termen, Gleichungen (Jhg. 7–10). Abgerufen am 13.8.2025 von https://maco.dzlm.de/verstehensgrundlagen-zu-variablen-termen-gleichungen
MAHIKO. (o.J.). Division verstehen – Grundlagen. Abgerufen am 11.2.2025 von https://mahiko.dzlm.de/2-schuljahr-–-überblick/division-verstehen/grundlagen
MAHIKO. (o.J.). Geteiltaufgaben an der Punktereihe. Abgerufen am 11.2.2025 von https://mahiko.dzlm.de/node/430
MAHIKO. (o.J.). Malaufgaben sortieren. Abgerufen am 11.2.2025 von https://mahiko.dzlm.de/sites/mahiko/files/uploads/2_schuljahr/SicherimEinmaleins/pdf/2sj_sicherimeinmaleins_uebungen_1_220504.pdf
MAHIKO. (o.J.). Multiplikation verstehen – Grundlagen. Abgerufen am 11.2.2025 von https://mahiko.dzlm.de/2-schuljahr-–-überblick/multiplikation-verstehen/grundlagen
MAHIKO. (o.J.). Multiplikation verstehen – Übungen. Abgerufen am 11.2.2025 von https://mahiko.dzlm.de/2-schuljahr-–-überblick/multiplikation-verstehen/übungen
MAHIKO. (o.J.). Schwierige Geteiltaufgaben lösen. Abgerufen am 11.2.2025 von https://mahiko.dzlm.de/node/431
MAHIKO. (o.J.). Sicher im 1 + 1. Abgerufen am 1.3.2025 von https://mahiko.dzlm.de/1-schuljahr-–-überblick/sicher-im-1-plus-1/grundlagen
MAHIKO. (o.J.). Sicher im 1 × 1 – Grundlagen. Abgerufen am 11.2.2025 von https://mahiko.dzlm.de/2-schuljahr-–-überblick/sicher-im-1-durch-1/grundlagen
Mathe 2000. (o.J.). Einmaleinstafel. Abgerufen am 1.3.2025 von https://www.mathe2000.de/rechenposter-einspluseins-und-einmaleins
Mathe inklusiv mit PIKAS. (o.J.). Langfristig denken – Hintergrund. Abgerufen am 13.8.2025 von https://pikas-mi.dzlm.de/leitideen/kontinuit%C3%A4t-herstellen/unterricht-langfristig-denken/hintergrund
Mathe inklusiv mit PIKAS. (o.J.). Negative Zahlen. Abgerufen am 13.8.2025 von https://pikas-mi.dzlm.de/inhalte/negative-zahlen
Mathe inklusiv mit PIKAS. (o.J.). Plus-Minus-Spiel zu den negativen Zahlen. Abgerufen am 13.8.2025 von https://pikas-mi.dzlm.de/inhalte/negative-zahlen/unterricht/plus-minus-spiel
Mathe sicher können. (o.J.). Brüche, Prozente und Dezimalzahlen. Abgerufen am 13.8.2025 von https://mathe-sicher-koennen.dzlm.de/material-sek/brueche-prozente-und-dezimalzahlen
Mathe sicher können. (o.J.). Natürliche Zahlen. Abgerufen am 13.8.2025 von https://mathe-sicher-koennen.dzlm.de/material-sek/natuerliche-zahlen
Mathe sicher können. (o.J.). Sachrechnen. Abgerufen am 13.8.2025 von https://mathe-sicher-koennen.dzlm.de/material-sek/sachrechnen
Mathematische Basteleien. (o.J.). Dreiecke. Abgerufen am 13.8.2025 von https://www.mathematische-basteleien.de/dreieck.htm
Mein-lernen (o.J.). Rationale vs. irrationale Zahlen – Faktencheck im Vergleich. Abgerufen am 11.9.2025 von https://mein-lernen.at/faktencheck-mathematik/rationale-vs-irrationale-zahlen-faktencheck-im-vergleich/
Ministerium für Kultur, Jugend und Sport Baden-Württemberg (Hrsg.). (2022). Alles zählt! Mathe im Kita-Alltag – Startseite. Abgerufen am 17.4.2025 von https://ibbw-bw.de/,Lde/Startseite/Empirische-Bildungsforschung/alles-zaehlt
Ministerium für Kultur, Jugend und Sport Baden-Württemberg. (o.J.). Alles zählt! Mathe im Kita-Alltag. Abgerufen am 22.4.2025 von https://kindergaerten.kultus-bw.de/,Lde/Foerderung+mathematischer+Kompetenzen
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Hrsg.). (2022). Aufgabenfeld Mathematik in den Unterrichtsvorgaben für den zieldifferenten Bildungsgang geistige Entwicklung an allen Lernorten in NRW. Abgerufen am 22.4.2025 von https://www.schulentwicklung.nrw.de/lehrplaene/lehrplan/319/zdbg_ge_m_uvorgaben_2022_06_08.pdf
MNU – Verband zur Förderung des MINT-Unterrichts. (o.J.). Satz des Thales. Abgerufen am 13.8.2025 von https://www.mnu.de/weko/5-2_thales.pdf
Müller-Wolfangel, U., & Schreiber, B. (2014). Duden – Basiswissen Grundschule Mathematik: Nachschlagen und Üben Klasse 1–4 (3., aktual. Aufl.). Dudenverlag.
Padberg, F., & Wartha, S. (2017). Didaktik der Bruchrechnung (5. Aufl.). Springer. https://doi.org/10.1007/978-3-662-52969-0
Peter-Koop, A., et al. (2007). Diagnostische Materialien und Handreichungen zum Konzept des EMBI (ElementarMathematischesBasisInterview) für die Bereiche KiGa, Größen-Messen-Raum und Form, Zahlen und Operationen. Mildenberger. Abgerufen am 12.1.2025 von https://www.mildenberger-verlag.de/page.php?modul=GoShopping&op=show_rubrik&cid=863
Peter-Koop, A., Lilitakis, G., & Spindeler, B. (Hrsg.). (2009). Lernumgebungen – Ein Weg zum kompetenzorientierten Mathematikunterricht in der Grundschule. Mildenberger.
Piaget, J. & Szeminska, A. (1975). Die Entwicklung des Zahlenbegriffs beim Kinde. Klett-Cotta.
PIKAS. (o.J.). 1 plus 1 richtig üben. Abgerufen am 1.3.2025 von https://pikas.dzlm.de/pikasfiles/uploads/upload/Material/gesamtes_Material/1plus1richtig_ueben.pdf
PIKAS. (o.J.). Aufbau eines tragfähigen Stellenwertverständnisses (Taskcard). Abgerufen am 1.3.2025 von https://www.taskcards.de/#/board/49a9b084-32bb-45ec-bbaa-3cb472684f74/view?token=199f004a-89fe-414f-b3b4-65b2bff04303
PIKAS. (o.J.). Daten und Diagramme. Abgerufen am 22.4.2025 von https://pikas-kompakt.dzlm.de/themenhäuser/daten-und-diagramme#toc–material-und-informationen-OpPqC_Hl
PIKAS. (o.J.). Daten, Häufigkeiten und Wahrscheinlichkeiten. Abgerufen am 22.4.2025 von https://pikas.dzlm.de/unterricht/daten-häufigkeiten-und-wahrscheinlichkeiten/wahrscheinlichkeiten/kombinatorik
PIKAS. (o.J.). Division. Abgerufen am 11.2.2025 von https://pikas.dzlm.de/unterricht/distanzunterricht/zentrale-themen-2-schuljahr/division
PIKAS. (o.J.). Eigenschaften von Formen. Abgerufen am 22.4.2025 von https://pikas-mi.dzlm.de/inhalte/formen-erkunden/hintergrund
PIKAS. (o.J.). Eins durch eins richtig üben. Abgerufen am 11.2.2025 von https://pikas.dzlm.de/pikasfiles/uploads/upload/Material/Haus_3_-Umgang_mit_Rechenschwierigkeiten/UM/basisinfo_1_1_neu.pdf
PIKAS. (o.J.). Einspluseinstafel. Abgerufen am 1.3.2025 von https://pikas-mi.dzlm.de/pikasmifiles/uploads/Leitideen/Effektiv-ueben/Material/einspluseins-tafel.pdf
PIKAS. (o.J.). Fachwortschatz Mathematik. Abgerufen am 1.3.2025 von https://pikas.dzlm.de/pikasfiles/uploads/upload/Material/Haus_7-Gute-Aufgaben/IM/Informationstexte/IM_Redemittel_erstes_Schuljahr_neu.pdf
PIKAS. (o.J.). Formen und Körper. Abgerufen am 4.4.2025 von https://pikas.dzlm.de/pikasfiles/uploads/upload/Material/unterricht_neu/schulanfang/um_schulanfang_karteikarten_formenundkoerper.pdf
PIKAS. (o.J.). Geld. Abgerufen am 10.4.2025 von https://pikas-mi.dzlm.de/node/307
PIKAS. (o.J.). Größen und Messen. Abgerufen am 1.3.2025 von https://pikas.dzlm.de/unterricht/größen-und-messen
PIKAS. (o.J.). Grundlagen sichern: Unterricht. Abgerufen am 1.3.2025 von https://pikas-mi.dzlm.de/leitideen/kontinuität-herstellen/grundlagen-sichern/unterricht
PIKAS. (o.J.). Gute Aufgaben im Geometrie-Unterricht. Abgerufen am 4.4.2025 von https://pikas.dzlm.de/pikasfiles/uploads/handout_gute_aufgaben_im_geometrieunterricht.pdf
PIKAS. (o.J.). Guter Matheunterricht. Abgerufen am 1.3.2025 von https://pikas.dzlm.de/selbststudium/entdecken-beschreiben-begründen
PIKAS. (o.J.). Kompetenzaufbau im Kontext „Symmetrie“. Abgerufen am 9.2.2025 von https://pikas.dzlm.de/pikasfiles/uploads/doc/Modul%202.3%20(Langfristiger%20Kompetenzaufbau%20an%20fundamentaler%20Idee%20Symmetrie).pdf
PIKAS. (o.J.). Kompetenzübersicht und Lernziele. Abgerufen am 4.4.2025 von https://pikas.dzlm.de/pikasfiles/uploads/upload/Material/unterricht_neu/schulanfang/230531_ubersicht_teilkompetenzen_mathematik_am_schulanfang.pdf
PIKAS. (o.J.). Längenbegriff. Abgerufen am 10.4.2025 von https://pikas-mi.dzlm.de/inhalte/größen-messen-längen/hintergrund/grundlagen
PIKAS. (o.J.). Lesen und Interpretieren. Abgerufen am 4.4.2025 von https://pikas.dzlm.de/unterricht/daten-häufigkeiten-und-wahrscheinlichkeiten/daten-und-diagramme/lesen-und-interpretieren
PIKAS. (o.J.). Materialien nichtzählendes Rechnen 1 + 1 und 1 – 1 [TaskCard]. Abgerufen am 1.3.2025 von https://www.taskcards.de/#/board/805dce4d-f18d-4797-8f7c-445321d0cf98/view?token=e10851f8-3131-4d94-8da2-f4e589000035
PIKAS. (o.J.). Mathe – ein Kinderspiel. Abgerufen am 1.3.2025 von https://pikas.dzlm.de/pikasfiles/uploads/upload/Material/Haus_1_-Entdecken_Beschreiben_Begruenden/IM/Elternratgeber/Elternratgeber_A4.pdf
PIKAS. (o.J.). Mathe gemeinsam lernen. Abgerufen am 1.3.2025 von https://pikas.dzlm.de/pikasfiles/uploads/Dokumente/buch/handreichung-mathematik-gemeinsam-lernen.pdf
PIKAS. (o.J.). Mathe in den Kopf. Abgerufen am 1.3.2025 von https://pikas.dzlm.de/pikasfiles/uploads/upload/Material/Haus_3-Umgang_mit_Rechenschwierigkeiten/FM/Sachinfo%20Mathe%20in%20den%20Kopf_0.pdf
PIKAS. (o.J.). Mathe-Konferenzen. Abgerufen am 1.3.2025 von https://pikas.dzlm.de/pikasfiles/uploads/upload/Material/Haus_8-Guter_Unterricht/UM/Mathe-Konferenzen/Basisinfos/Infopapier_Mathekonferenzen_2017_NEU.pdf
PIKAS. (o.J.). Mathekartei. Abgerufen am 4.4.2025 von https://pikas.dzlm.de/unterricht/mathekartei
PIKAS. (o.J.). Muster. Abgerufen am 10.4.2025 von https://pikas.dzlm.de/unterricht/raum-und-form/ebene-figuren/muster
PIKAS. (o.J.). Rechengeschichten. Abgerufen am 1.3.2025 von https://pikas.dzlm.de/pikasfiles/uploads/upload/Material/Haus_7-Gute-Aufgaben/IM/Informationstexte/Rechengeschichten-schreiben,bearbeiten,rueckmelden,bewerten.pdf
PIKAS. (o.J.). Sammeln und Darstellen. Abgerufen am 20.3.2025 von https://pikas.dzlm.de/unterricht/daten-häufigkeiten-und-wahrscheinlichkeiten/daten-und-diagramme/sammeln-und-darstellen
PIKAS. (o.J.). Schnell sehen. Abgerufen am 1.3.2025 von https://pikas.dzlm.de/diagnose-und-förderung/zahlraum-bis-20/zahlverständnis/zahlen-schnell-sehen
PIKAS. (o.J.). Sicher im 1 + 1. Abgerufen am 1.3.2025 von https://pikas.dzlm.de/unterricht/zahlen-und-operationen/zahlraum-bis-20/sicher-im-11
PIKAS. (o.J.). Standortbestimmung. Abgerufen am 1.3.2025 von https://pikas.dzlm.de/diagnose-und-förderung/födima-schuljahre-1-2/standortbestimmungen-kartei-und-handreichung
PIKAS. (o.J.). Stützpunktvorstellungen aufbauen. Abgerufen am 13.8.2025 von https://pikas.dzlm.de/unterricht/st%C3%BCtzpunktvorstellungen-aufbauen
PIKAS. (o.J.). Vorschulische mathematikbezogene Grundkompetenzen. Abgerufen am 1.3.2025 von https://pikas.dzlm.de/unterricht/schulanfang/frühe-mathematische-bildung
PIKAS. (o.J.). Wahrscheinlichkeiten und Zufallsexperimente. Abgerufen am 4.4.2025 von https://pikas.dzlm.de/unterricht/daten-häufigkeiten-und-wahrscheinlichkeiten/wahrscheinlichkeiten/zufallsexperimente
PIKAS. (o.J.). Wortspeicher (Übersicht). Abgerufen am 10.3.2025 von https://pikas.dzlm.de/pikasfiles/uploads/upload/Material/Haus_7-Gute–Aufgaben/IM/Informationstexte/IM_Redemittel_erstes_Schuljahr_neu.pdf
PIKAS. (o.J.). Wortspeicher (Video). Abgerufen am 1.3.2025 von https://pikas.dzlm.de/wortspeicher
PIKAS. (o.J.). Würfeltürme. Abgerufen am 22.4.2025 von https://pikas.dzlm.de/pikasfiles/uploads/upload/Material/unterricht_neu/schulanfang/um_schulanfang_arbeitsblatt_mustertuerme.pdf
PIKAS. (o.J.). Zahlverständnis im Anfangsunterricht. Abgerufen am 1.3.2025 von https://pikas-kompakt.dzlm.de/themenhäuser/zahlverständnis-anfangsunterricht#toc–material-und-informationen-OpPqC_Hl
PIKAS. (o.J.). Zeichnen. Abgerufen am 4.4.2025 von https://pikas.dzlm.de/unterricht/raum-und-form/zeichnen
Prenzel, M. & Blum, W. (2007). Entwicklung eines Testverfahrens zur Überprüfung der Bildungsstandards in Mathematik für den Mittleren Schulabschluss. Technischer Bericht. IPN.
PRIMAKOM (o.J.). Das Haus der Vierecke. Abgerufen am 11.9.2025 von https://primakom.dzlm.de/primafiles/uploads/Dokumente/EbeneFiguren_Hintergrund_Tabelle%20Haus%20der%20Vierecke.pdf
PRIMAKOM. (o.J.). Darstellungswechsel. Abgerufen am 10.4.2025 von https://primakom.dzlm.de/inhalte/raum-und-form/körper/einstieg
PRIMAKOM. (o.J.). Ebene Figuren. Abgerufen am 20.3.2025 von https://primakom.dzlm.de/inhalte/raum-und-form/ebene-figuren/einstieg
PRIMAKOM. (o.J.). Größen und Messen. Abgerufen am 4.4.2025 von https://primakom.dzlm.de/inhalte/größen-und-messen/zum-sachrechnen-der-grundschule/hintergrund
PRIMAKOM. (o.J.). Größenbuch. Abgerufen am 10.4.2025 von https://primakom.dzlm.de/node/65
PRIMAKOM. (o.J.). Hintergrund Kombinatorik. Abgerufen am 20.3.2025 von https://primakom.dzlm.de/aufgabenformate/bunte-türme-bauen/einstieg/einstieg/hintergrund
PRIMAKOM. (o.J.). Raum und Form. Abgerufen am 4.4.2025 von https://primakom.dzlm.de/inhalte/raum-und-form
PRIMAKOM. (o.J.). Raumorientierung. Abgerufen am 4.4.2025 von https://primakom.dzlm.de/inhalte/raum-und-form/raumorientierung/einstieg
PRIMAKOM. (o.J.). Symmetrie in der Grundschule. Abgerufen am 4.4.2025 von https://primakom.dzlm.de/inhalte/raum-und-form/symmetrie/hintergrund
PRIMAKOM. (o.J.). Vom Raum in die Ebene. Abgerufen am 4.4.2025 von https://primakom.dzlm.de/inhalte/raum-und-form/ebene-figuren/einstieg
PRIMAKOM. (o.J.). Wortspeicher Raum und Form. Abgerufen am 11.3.2025 von https://primakom.dzlm.de/node/452#sprachliche
PRIMAKOM. (o.J.). Zeichnen. Abgerufen am 4.4.2025 von https://primakom.dzlm.de/inhalte/größen-und-messen/zeichnen/hintergrund
PRIMAKOM. (o.J.). Zufall und Wahrscheinlichkeiten. Abgerufen am 4.4.2025 von https://primakom.dzlm.de/inhalte/daten-häufigkeit-wahrscheinlichkeit/zufall-und-wahrscheinlichkeit/hintergrund
Radatz, H. & Schipper, W. (1983). Handbuch für den Mathematikunterricht an Grundschulen. Schroedel.
Rasch, R., & Sitter, K. (2020). Module für den Geometrieunterricht in der Grundschule: Geometrie handlungsorientiert unterrichten und beziehungshaltig entdecken (3. Aufl.). Klett Kallmeyer.
Reichel, S. (2017). Gute Aufgaben im Mathematikunterricht. Auer.
Reiss, K.; Heinze, A. & Pekrun, R. (2007). Mathematische Kompetenz und ihre Entwicklung in der Grundschule. In M. Prenzel, I. Goglin & H.-H. Kruger (Hrsg.), Kompetenzdiagnostik. Zeitschrift für Erziehungswissenschaft 10, Sonderheft 8, 107-127.
Resnick, L. B. (1989). Developing mathematical knowledge. American Psychologist (44), 162-169.
Reuter, S., & Neubert, B. (2010). Große Körper können leicht, kleine können schwer sein: Zur Entwicklung von Größenvorstellungen in der Grundschule. Grundschulunterricht Mathematik, 57(4), 4–7.
Roth, J. (2012). Geometrische Körper erkennen und sortieren als Grundlage der Begriffsbildung. Fördermagazin, 2, 13–17. Abgerufen am 5.2.2025 von https://juergen-roth.de/veroeffentlichungen/2012/roth_geometrische_koerper_erkennen_und_sortieren_als_grundlage_der_begriffsbildung.pdf
Royar, T. (2012). Wo Piaget irrte: Zahlbegriffsentwicklung im Vorschulalter. Abgerufen am 1.3.2025 von https://www.kita-fachtexte.de/de/fachtexte-finden/wo-piaget-irrte-zahlbegriffsentwicklung-im-vorschulalter
Royar, T. (2016). Wenn Vereinfachung zur Verfälschung wird: Wider die Banalisierung elementarer Mathematik. Abgerufen am 1.3.2025 von https://www.kita-fachtexte.de/de/fachtexte-finden/wenn-vereinfachung-zur-verfaelschung-wird-wider-die-banalisierung-elementarer-mathematik
Schäfer, H. (2020). Mathematik und geistige Behinderung. Kohlhammer.
Schindler, F., & Schindler, M. (2022). Diagnostische Interviews bei Schwierigkeiten im Rechnenlernen (DIBS-R): Ein Praxiskonzept für den Beginn der Sekundarstufe I. In M. Gebhard, D. Scheer & M. Schurig (Hrsg.), Handbuch der sonderpädagogischen Diagnostik (S. 857–869). Abgerufen am 24.1.2025 von https://www.researchgate.net/publication/366138998_Diagnostische_Interviews_bei_Schwierigkeiten_im_Rechnenlernen_DIBS-R-_Ein_Praxiskonzept_fur_den_Beginn_der_Sekundarstufe_I#fullTextFileContent
Schneider, W.; Küspert, P. & Krajewski, K. (2021). Die Entwicklung mathematischer Kompetenzen (3. Aufl.). Utb.
Schulz, A. & Wartha, S. (2021). Zahlen & Operationen am Übergang Primar-Sekundarstufe. Springer Spektrum.
Selter, C. (2017). Guter Mathematikunterricht – Konzeptionelles und Beispiele aus dem Projekt PIKAS. Cornelsen.
Selter, C., Prediger, S., Nührenbörger, M., & Hußmann, S. (2014). Auszug N4a: Ich kann Multiplikations-Aufgaben zu Situationen finden und umgekehrt. In Mathe sicher können. Handreichungen für ein Diagnose- und Förderkonzept zur Sicherung mathematischer Basiskompetenzen: Natürliche Zahlen. Abgerufen am 26.1.2025 von https://mathe-sicher-koennen.dzlm.de/mskfiles/uploads/Dokumente/mskgs_n4a_1_hru_n4_a_130920.pdf
Siegler, R. S. (1998). Children´s thinking. Prentice Hall.
SiMa (o.J.). Flächeninhaltsformel für Rechtecke verstehen und begründen. Abgerufen am 13.8.2025 von https://sima.dzlm.de/sites/simams/files/uploads/sima5-005-unterrichtsmaterial-flaecheninhaltsformel-231118.pdf
SiMa (o.J.). Strategien zum Verstehen von Textaufgaben. Abgerufen am 11.9.2025 von https://sima.dzlm.de/sites/simams/files/uploads/sima5_textaufgaben-did-kommentar_190313.pdf
SiMa (o.J.). Unterrichtsmaterialien Sekundarstufe. Abgerufen am 13.8.2025 von https://sima.dzlm.de/unterricht/unterrichtsmaterialien-sekundarstufe
Spiegel, H. Selter, C. (2003). Kinder und Mathematik. Was Erwachsene wissen sollten. Klett Kallmeyer.
Staatsinstitut für Schulqualität und Bildungsforschung (ISB) (2008). Daten, Häufigkeit und Wahrscheinlichkeit. München. Abgerufen am 10.3.2025 von https://www.isb.bayern.de/fileadmin/user_upload/Grundschule/Handreichung_Daten/hr_Daten_Haeufigkeit_2008.pdf
Steinweg, A. (2008). Mathe aktiv! Mathematik in Alltagssituationen in TransKiGs-Kindertagesstätten. Abgerufen am 1.3.2025 von https://bildungsserver.berlin-brandenburg.de/fileadmin/bbb/schule/schulentwicklung/Modellversuche_Schulversuche/transkigs/Instrumente/Mathe_aktiv_2008.pdf
Stiftung „Haus der kleinen Forscher“ (2014). Mathematik in Raum und Form entdecken. Mathematisches Denken von Kita- und Grundschulkindern unterstützen. Abgerufen am 11.9.2025 von https://campus.stiftung-kinder-forschen.de/pluginfile.php/1945/engage_article/content/72/broschuere_mathematik_in_raum_und_form%20%281%29.pdf
Stiftung „Haus der kleinen Forscher“ (2016). Zahlen, Zählen, Rechnen –Mathematik entdecken. 2. Auflage. Abgerufen am 11.9.2025 von https://campus.stiftung-kinder-forschen.de/pluginfile.php/1945/engage_article/content/67/broschuere_zahlen_zaehlen_rechnen%20%281%29.pdf
Stiftung „Haus der kleinen Forscher“ (2023). Mathematik ist machbar. Praxisnahe Bausteine für kreative Lernbegleitung. Abgerufen am 11.9.2025 von https://campus.stiftung-kinder-forschen.de/pluginfile.php/1945/engage_article/content/363/broschuere_mathematik_ist_machbar.pdf
Studienkreis (o.J.). Was sind rationale Zahlen? Eine einfache Erklärung. Abgerufen am 11.9.2025 von https://www.studienkreis.de/mathematik/rationale-zahlen/
Studienkreis (o.J.). Wie lauten die Kongruenzsätze? Abgerufen am 11.9.2025 von https://www.studienkreis.de/mathematik/kongruenz-aehnlichkeit-figuren/
Ufer, S.; Reiss, K. & Heinze, A. (2009). BIGMATH – Ergebnisse zur Entwicklung mathematischer Kompetenz in der Primarstufe. In A. Heinze. & M. Grusing (Hrsg.), Mathematiklernen vom Kindergarten bis zum Studium. Kontinuität und Kohärenz als Herausforderung für den Mathematikunterricht (S. 61-85). Waxmann.
Weis, I. (2020). Sprachförderung PLUS- Förderbausteine für den Soforteinsatz im Mathematikunterricht. Klett.
Wittmann E., Müller, G. (o.J.) Blitzrechenoffensive! Abgerufen am 1.3.2025 von https://wwwold.mathematik.tu-dortmund.de/ieem/mathe2000/pdf/Blitzrechenoffensive.pdf
Wittmann, E. (1994). Wider die Flut der „bunten Hunde“ und der „grauen Päckchen“. Die Konzeption des aktiv-entdeckenden Lernens und des produktiven Übens. Abgerufen am 13.1.2025 von https://www.mathe2000.de/sites/default/files/Wider%20die%20Flut%20der%20bunten_Hunde.pdf
Wittmann, E. (o.J.). Produktives Üben. Abgerufen am 1.3.2025 von https://www.mathe2000.de/sites/default/files/Ergaenzung-zum-HB.pdf
Wittmann, E. C. & Müller, G. N. (2022). Handbuch produktiver Rechenübungen. Ernst Klett.
Wittmann, E. u.a. (o.J.). Offene Sachaufgaben. Abgerufen am 1.3.2025 von https://www.mathe2000.de/sites/default/files/OffeneSachaufgaben-jenseits-Fermi-Aufgaben.pdf
Wittmann, E., Müller, G. (2019). Handbuch produktiver Rechenübungen. Klett.
Wittmann, E., Müller, G. (o.J.). Rechenposter. Abgerufen am 1.3.2025 von https://www.mathe2000.de/rechenposter-einspluseins-und-einmaleins
Wollring, B. & Rinkens, H.D. (2008). Raum und Form. In: G. Walter, M., van den Heuwel-Panhuizen, D. Granzer & O. Köller (Hrsg.), Bildungsstandards für die Grundschule: Mathematik konkret (S.118-140). Cornelsen Scriptor.
Wollring, B., Peter-Koop, A., Haberzettl, N., Becker, N., & Spindeler, B. (2011). Elementarmathematisches Basisinterview. Größen und Messen, Raum und Form. Mildenberger.
Zeindl-Steiner, R. (2012). Eine Lernspur durch den Zahlenraum 10. Abgerufen am 1.3.2025 von https://www.edugroup.at/fileadmin/DAM/Gegenstandsportale/Volksschule/Dateien/Mathematik/Lernspur__durch_den_Zahlenraum_10.pdf
ZUM (2022). Kongruenz von Dreiecken. Abgerufen am 13.8.2025 von https://unterrichten.zum.de/wiki/Kongruenz_von_Dreiecken

Zum Inhaltsverzeichnis zurück

Titelbild: Wikipedia:
https://de.wikipedia.org/wiki/Euklid#/media/Datei:Euclid,_Elements_10,_appendix.jpg
https://de.wikipedia.org/wiki/Pythagoras#/media/Datei:Pythagoras-M%C3%BCnz.JPG

Inhaltsverzeichnis

1. Abkürzungsverzeichnis

2. Einleitung

Stufenmodelle

Teilbereiche

Basale Anfänge der mathematischen Kompetenzentwicklung

3. Tabellarische Stufenmodelle

Teilbereich A: Lernende in Individualität und Persönlichkeitsentwicklung

Teilbereich B: Lernende in sozialen Beziehungen

Teilbereich C: Lernende im Verhältnis zu Kulturen und Religionen

Teilbereich D: Lernende in ihrem Verhältnis zur Umwelt und Zeit

3. Tabellarische Stufenmodelle

Tabelle 3.1 Stufenmodell zum Teilbereich: Zahl und Operation

Teilbereich: Zahlen und Operationen (ZuO)

Pädagogische Angebote

Sinnliche Welterkundung

Welterkundung durch unspezifisches Operieren

Welterkundung durch spezifisches Hantieren

Zahliges Handeln auf konkreter Ebene

Tabelle 3.2: Größen und Messen

Tabelle 3.3: Raum und Form

Tabelle 3.4: Daten und Zufall

Tabelle 3.5: Strukturen und funktionaler Zusammenhang

4. Führerscheine für die Hand der Kinder

5. Exemplarische Entwürfe für das Lernen am gemeinsamen Gegenstand

Gemeinsame Lernsequenzen – von- und miteinander Lernen

6. Entwürfe für die Arbeit an Themen und Interessen der Kinder

Materialwimmelkisten

Schätzglas

Naturmaterialien

7. Kommentierter Überblick über Stufenmodelle

7.1: Basaler Zugang zum mathematischen Kompetenzerwerb

7.2: Elementarer Zugang zum mathematischen Kompetenzerwerb

7.3: Primarer Zugang zum mathematischen Kompetenzerwerb

7.4: Sekundarer Zugang zum mathematischen Kompetenzerwerb

7.5: Weitere Stufenmodelle

8. Literaturverzeichnis

Links zu bewährten Online-Materialien für den Mathematikunterricht:

Literaturverzeichnis: